最长回文子串解法详解
2015-09-24 21:20
741 查看
回文串,就是指正读和反读都一样的字符串,比如
那么,如何求一个字符串的最长回文子串(Longest Palindromic Substring)?这里我们有多种解法。
暴力解法就是直接枚举所有子串,对每个子串判断是否为回文,时间复杂度为O(n3)。
这是最糟糕的方法,相信面试官问你这个问题,绝对不是想要这个答案。
动态规划法是在暴力解法上进行的优化。通过记录一些我们需要的东西,来避免暴力解法中很多重复的判断。
假设 dp[i][j] 表示子串 s[i…j] 是否是回文,那么对于动态规划表 dp 的打表方式如下:

C++代码如下
回文字符串的子串也是回文,比如P[i,j](表示以i开始以j结束的子串)是回文字符串,那么P[i+1,j-1]也是回文字符串。这样最长回文子串就能分解成一系列子问题了。这样需要额外的空间O(N^2),算法复杂度也是O(N^2)。
首先定义状态方程和转移方程:
P[i,j]=0表示子串[i,j]不是回文串。P[i,j]=1表示子串[i,j]是回文串。
P[i,i]=1
P[i,j] =
P[i+1,j-1], if(s[i]==s[j])
=
0 ,
if(s[i]!=s[j])
这个算法思想其实很简单,就是对给定的字符串S,分别以该字符串S中的每一个字符 c 为中心,向两边扩展,记录下以字符 c 为中心的回文子串的长度。时间复杂度为O(n2),空间复杂度仅为O(1)。
但有一点需要注意的是,回文的情况可能是 a b a,也可能是 a b b a。
另外,据说还有一个很巧妙的算法,叫Manacher算法,可以在 O(n) 的时间复杂度里求出最长回文子串。
Manacher法只能解决例如aba这样长度为奇数的回文串,对于abba这样的不能解决,于是就在里面添加特殊字符。我是添加了“#”,使abba变为a#b#b#a。这个算法就是利用已有回文串的对称性来计算的,具体算法复杂度为O(N),我没看出来,因为有两个嵌套的for循环。
具体原理参考这里。测试代码中没过滤掉“#”。
Manacher算法能够在O(N)的时间复杂度内得到一个字符串以任意位置为中心的回文子串。其算法的基本原理就是利用已知回文串的左半部分来推导右半部分。
首先,在字符串s中,用rad[i]表示第i个字符的回文半径,即rad[i]尽可能大,且满足:
s[i-rad[i],i-1]==s[i+1,i+rad[i]]
很明显,求出了所有的rad,就求出了所有的长度为奇数的回文子串.
至于偶数的怎么求,最后再讲.
假设现在求出了rad[1..i-1],现在要求后面的rad值,并且通过前面的操作,得知了当前字符i的rad值至少为j.现在通过试图扩大j来扫描,求出了rad[i].再假设现在有个指针k,从1循环到rad[i],试图通过某些手段来求出[i+1,i+rad[i]]的rad值.
根据定义,黑色的部分是一个回文子串,两段红色的区间全等.
因为之前已经求出了rad[i-k],所以直接用它.有3种情况:

①rad[i]-k<rad[i-k]
如图,rad[i-k]的范围为青色.因为黑色的部分是回文的,且青色的部分超过了黑色的部分,所以rad[i+k]肯定至少为rad[i]-k,即橙色的部分.那橙色以外的部分就不是了吗?这是肯定的.因为如果橙色以外的部分也是回文的,那么根据青色和红色部分的关系,可以证明黑色部分再往外延伸一点也是一个回文子串,这肯定不可能,因此rad[i+k]=rad[i]-k.为了方便下文,这里的rad[i+k]=rad[i]-k=min(rad[i]-k,rad[i-k]).

②rad[i]-k>rad[i-k]
如图,rad[i-k]的范围为青色.因为黑色的部分是回文的,且青色的部分在黑色的部分里面,根据定义,很容易得出:rad[i+k]=rad[i-k].为了方便下文,这里的rad[i+k]=rad[i-k]=min(rad[i]-k,rad[i-k]).
根据上面两种情况,可以得出结论:当rad[i]-k!=rad[i-k]的时候,rad[i+k]=min(rad[i]-k,rad[i-k]).
注意:当rad[i]-k==rad[i-k]的时候,就不同了,这是第三种情况:

如图,通过和第一种情况对比之后会发现,因为青色的部分没有超出黑色的部分,所以即使橙色的部分全等,也无法像第一种情况一样引出矛盾,因此橙色的部分是有可能全等的,但是,根据已知的信息,我们不知道橙色的部分是多长,因此就把i指针移到i+k的位置,j=rad[i-k](因为它的rad值至少为rad[i-k]),等下次循环的时候再做了.
整个算法就这样.
至于时间复杂度为什么是O(n),我已经证明了,但很难说清楚.所以自己体会吧.
上文还留有一个问题,就是这样只能算出奇数长度的回文子串,偶数的就不行.怎么办呢?有一种直接但比较笨的方法,就是做两遍(因为两个程序是差不多的,只是rad值的意义和一些下标变了而已).但是写两个差不多的程序是很痛苦的,而且容易错.所以一种比较好的方法就是在原来的串中每两个字符之间加入一个特殊字符,再做.如:aabbaca,把它变成(#a#a#b#b#a#c#a#),左右的括号是为了使得算法不至于越界。这样的话,无论原来的回文子串长度是偶数还是奇数,现在都变成奇数了.
算法导论,O(n)求解回文串
回文串定义:“回文串”是一个正读和反读都一样的字符串,比如“level”或者“noon”等等就是回文串。回文子串,顾名思义,即字符串中满足回文性质的子串。
经常有一些题目围绕回文子串进行讨论,比如POJ3974最长回文,求最长回文子串的长度。朴素算法是依次以每一个字符为中心向两侧进行扩展,显然这个复杂度是O(N^2)的,关于字符串的题目常用的算法有KMP、后缀数组、AC 自动机,这道题目利用扩展KMP可以解答,其时间复杂度也很快O(N*logN)。但是,今天笔者介绍一个专门针对回文子串的算法,其时间复杂度为O(n),这就是manacher
算法。
大家都知道,求回文串时需要判断其奇偶性,也就是求aba 和abba 的算法略有差距。然而,这个算法做了一个简单的处理,很巧妙地把奇数长度回文串与偶数长度回文串统一考虑,也就是在每个相邻的字符之间插入一个分隔符,串的首尾也要加,当然这个分隔符不能再原串中出现,一般可以用‘#’或者‘$’等字符。例如:
原串:abaab
新串:#a#b#a#a#b#
这样一来,原来的奇数长度回文串还是奇数长度,偶数长度的也变成以‘#’为中心奇数回文串了。
接下来就是算法的中心思想,用一个辅助数组P 记录以每个字符为中心的最长回文半径,也就是P[i]记录以Str[i]字符为中心的最长回文串半径。P[i]最小为1,此时回文串为Str[i]本身。
我们可以对上述例子写出其P 数组,如下
新串: # a # b # a # a # b #
P[] : 1 2 1 4 1 2 5 2 1 2 1
我们可以证明P[i]-1 就是以Str[i]为中心的回文串在原串当中的长度。
证明:
1、显然L=2*P[i]-1 即为新串中以Str[i]为中心最长回文串长度。
2、以Str[i]为中心的回文串一定是以#开头和结尾的,例如“#b#b#”或“#b#a#b#”所以L 减去最前或者最后的‘#’字符就是原串中长度 的二倍,即原串长度为(L-1)/2,化简的P[i]-1。得证。 依次从前往后求得P 数组就可以了,这里用到了DP(动态规划)的思想,也就是求P[i] 的时候,前面的P[]值已经得到了,我们利用回文串的特殊性质可以进行一个大大的优化。
先把核心代码贴上:
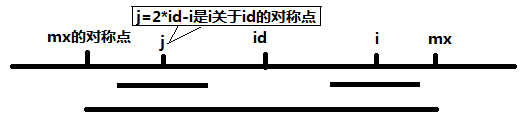
j=2*id-1 即为i 关于id 的对称点,根据对称性,P[j]的回文串也是可以对称到i 这边的,但是如果P[j]的回文串对称过来以后超过MaxId 的话,超出部分就不能对称过来了,如下图,
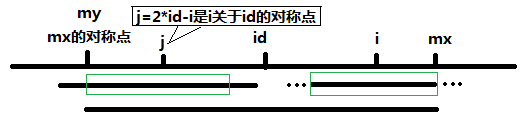
所以这里P[i]为的下限为两者中的较小者,p[i]=Min(p[2*id-i],MaxId-i)。算法的有效比较次数为MaxId 次,所以说这个算法的时间复杂度为O(n)。
具体代码,求解最长回文字符串的代码:
"level"或者
"noon"等等。
那么,如何求一个字符串的最长回文子串(Longest Palindromic Substring)?这里我们有多种解法。
解法一:暴力法
暴力解法就是直接枚举所有子串,对每个子串判断是否为回文,时间复杂度为O(n3)。这是最糟糕的方法,相信面试官问你这个问题,绝对不是想要这个答案。
string findLongestPalindrome(string &s)
{
int length=s.size();//字符串长度
int maxlength=0;//最长回文字符串长度
int start;//最长回文字符串起始地址
for(int i=0;i<length;i++)//起始地址
for(int j=i+1;j<length;j++)//结束地址
{
int tmp1,tmp2;
for(tmp1=i,tmp2=j;tmp1<tmp2;tmp1++,tmp2--)//判断是不是回文
{
if(s.at(tmp1)!=s.at(tmp2))
break;
}
if(tmp1>=tmp2&&j-i>maxlength)
{
maxlength=j-i+1;
start=i;
}
}
if(maxlength>0)
return s.substr(start,maxlength);//求子串
return NULL;
}
解法二:动态规划法O(n2)
动态规划法是在暴力解法上进行的优化。通过记录一些我们需要的东西,来避免暴力解法中很多重复的判断。假设 dp[i][j] 表示子串 s[i…j] 是否是回文,那么对于动态规划表 dp 的打表方式如下:

C++代码如下
string longestPalindrome(string s) {
int len = s.size();
if(len <= 1) return s;
// 动态规划表,全部初始化为true
vector<vector<bool>> dp(len, vector<bool>(len, true));
int start = 0, maxlen = 0;
for(int k=2; k<=len; ++k) { // 枚举子串的长度
for(int i=0; i<=len-k; ++i) { // 枚举子串起始位置
int j = i+k-1;
if(s[i] == s[j] && dp[i+1][j-1])
{
dp[i][j] = true;
start = i; // 记录回文子串的起点和长度
maxlen = k;
}
}
}
return s.substr(start, maxlen);
}回文字符串的子串也是回文,比如P[i,j](表示以i开始以j结束的子串)是回文字符串,那么P[i+1,j-1]也是回文字符串。这样最长回文子串就能分解成一系列子问题了。这样需要额外的空间O(N^2),算法复杂度也是O(N^2)。
首先定义状态方程和转移方程:
P[i,j]=0表示子串[i,j]不是回文串。P[i,j]=1表示子串[i,j]是回文串。
P[i,i]=1
P[i,j] =
P[i+1,j-1], if(s[i]==s[j])
=
0 ,
if(s[i]!=s[j])
string findLongestPalindrome(string &s)
{
const int length=s.size();
int maxlength=0;
int start;
bool P[50][50]={false};
for(int i=0;i<length;i++)//初始化准备
{
P[i][i]=true;
if(i<length-1&&s.at(i)==s.at(i+1))
{
P[i][i+1]=true;
start=i;
maxlength=2;
}
}
for(int len=3;len<length;len++)//子串长度
for(int i=0;i<=length-len;i++)//子串起始地址
{
int j=i+len-1;//子串结束地址
if(P[i+1][j-1]&&s.at(i)==s.at(j))
{
P[i][j]=true;
maxlength=len;
start=i;
}
}
if(maxlength>=2)
return s.substr(start,maxlength);
return NULL;
}
解法三:中心扩展法O(n2)
这个算法思想其实很简单,就是对给定的字符串S,分别以该字符串S中的每一个字符 c 为中心,向两边扩展,记录下以字符 c 为中心的回文子串的长度。时间复杂度为O(n2),空间复杂度仅为O(1)。但有一点需要注意的是,回文的情况可能是 a b a,也可能是 a b b a。
// 分别向左右扩展,返回扩展后的字符串
string expand(string s, int left, int right) {
int len = s.size();
while (left>=0 && right<len && s[left] == s[right])
{
left--;
right++;
}
return s.substr(left+1, right-left-1);
}
// 求最长回文子串
string longestPalindrome(string s) {
int len = s.size();
if(len<=1) return s;
string longest;
for (int i=0; i<len-1; i++)
{
string p1 = expand(s, i, i); // 奇数
if (p1.size() > longest.size())
longest = p1;
string p2 = expand(s, i, i+1); // 偶数
if (p2.size() > longest.size())
longest = p2;
}
return longest;
}string findLongestPalindrome(string &s)
{
const int length=s.size();
int maxlength=0;
int start;
for(int i=0;i<length;i++)//长度为奇数
{
int j=i-1,k=i+1;
while(j>=0&&k<length&&s.at(j)==s.at(k))
{
if(k-j+1>maxlength)
{
maxlength=k-j+1;
start=j;
}
j--;
k++;
}
}
for(int i=0;i<length;i++)//长度为偶数
{
int j=i,k=i+1;
while(j>=0&&k<length&&s.at(j)==s.at(k))
{
if(k-j+1>maxlength)
{
maxlength=k-j+1;
start=j;
}
j--;
k++;
}
}
if(maxlength>0)
return s.substr(start,maxlength);
return NULL;
}另外,据说还有一个很巧妙的算法,叫Manacher算法,可以在 O(n) 的时间复杂度里求出最长回文子串。
Manacher法
Manacher法只能解决例如aba这样长度为奇数的回文串,对于abba这样的不能解决,于是就在里面添加特殊字符。我是添加了“#”,使abba变为a#b#b#a。这个算法就是利用已有回文串的对称性来计算的,具体算法复杂度为O(N),我没看出来,因为有两个嵌套的for循环。具体原理参考这里。测试代码中没过滤掉“#”。
Manacher算法能够在O(N)的时间复杂度内得到一个字符串以任意位置为中心的回文子串。其算法的基本原理就是利用已知回文串的左半部分来推导右半部分。
首先,在字符串s中,用rad[i]表示第i个字符的回文半径,即rad[i]尽可能大,且满足:
s[i-rad[i],i-1]==s[i+1,i+rad[i]]
很明显,求出了所有的rad,就求出了所有的长度为奇数的回文子串.
至于偶数的怎么求,最后再讲.
假设现在求出了rad[1..i-1],现在要求后面的rad值,并且通过前面的操作,得知了当前字符i的rad值至少为j.现在通过试图扩大j来扫描,求出了rad[i].再假设现在有个指针k,从1循环到rad[i],试图通过某些手段来求出[i+1,i+rad[i]]的rad值.
根据定义,黑色的部分是一个回文子串,两段红色的区间全等.
因为之前已经求出了rad[i-k],所以直接用它.有3种情况:

①rad[i]-k<rad[i-k]
如图,rad[i-k]的范围为青色.因为黑色的部分是回文的,且青色的部分超过了黑色的部分,所以rad[i+k]肯定至少为rad[i]-k,即橙色的部分.那橙色以外的部分就不是了吗?这是肯定的.因为如果橙色以外的部分也是回文的,那么根据青色和红色部分的关系,可以证明黑色部分再往外延伸一点也是一个回文子串,这肯定不可能,因此rad[i+k]=rad[i]-k.为了方便下文,这里的rad[i+k]=rad[i]-k=min(rad[i]-k,rad[i-k]).

②rad[i]-k>rad[i-k]
如图,rad[i-k]的范围为青色.因为黑色的部分是回文的,且青色的部分在黑色的部分里面,根据定义,很容易得出:rad[i+k]=rad[i-k].为了方便下文,这里的rad[i+k]=rad[i-k]=min(rad[i]-k,rad[i-k]).
根据上面两种情况,可以得出结论:当rad[i]-k!=rad[i-k]的时候,rad[i+k]=min(rad[i]-k,rad[i-k]).
注意:当rad[i]-k==rad[i-k]的时候,就不同了,这是第三种情况:

如图,通过和第一种情况对比之后会发现,因为青色的部分没有超出黑色的部分,所以即使橙色的部分全等,也无法像第一种情况一样引出矛盾,因此橙色的部分是有可能全等的,但是,根据已知的信息,我们不知道橙色的部分是多长,因此就把i指针移到i+k的位置,j=rad[i-k](因为它的rad值至少为rad[i-k]),等下次循环的时候再做了.
整个算法就这样.
至于时间复杂度为什么是O(n),我已经证明了,但很难说清楚.所以自己体会吧.
上文还留有一个问题,就是这样只能算出奇数长度的回文子串,偶数的就不行.怎么办呢?有一种直接但比较笨的方法,就是做两遍(因为两个程序是差不多的,只是rad值的意义和一些下标变了而已).但是写两个差不多的程序是很痛苦的,而且容易错.所以一种比较好的方法就是在原来的串中每两个字符之间加入一个特殊字符,再做.如:aabbaca,把它变成(#a#a#b#b#a#c#a#),左右的括号是为了使得算法不至于越界。这样的话,无论原来的回文子串长度是偶数还是奇数,现在都变成奇数了.
#define min(x, y) ((x)<(y)?(x):(y))
#define max(x, y) ((x)<(y)?(y):(x))
string findLongestPalindrome3(string s)
{
int length=s.size();
for(int i=0,k=1;i<length-1;i++)//给字符串添加 #
{
s.insert(k,"#");
k=k+2;
}
length=length*2-1;//添加#后字符串长度
int *rad=new int[length]();
rad[0]=0;
for(int i=1,j=1,k;i<length;i=i+k)
{
while(i-j>=0&&i+j<length&&s.at(i-j)==s.at(i+j))
j++;
rad[i]=j-1;
for(k=1;k<=rad[i]&&rad[i-k]!=rad[i]-k;k++)//镜像,遇到rad[i-k]=rad[i]-k停止,这时不用从j=1开始比较
rad[i+k]=min(rad[i-k],rad[i]-k);
j=max(j-k,0);//更新j
}
int max=0;
int center;
for(int i=0;i<length;i++)
{
if(rad[i]>max)
{
max=rad[i];
center=i;
}
}
return s.substr(center-max,2*max+1);
}算法导论,O(n)求解回文串
回文串定义:“回文串”是一个正读和反读都一样的字符串,比如“level”或者“noon”等等就是回文串。回文子串,顾名思义,即字符串中满足回文性质的子串。
经常有一些题目围绕回文子串进行讨论,比如POJ3974最长回文,求最长回文子串的长度。朴素算法是依次以每一个字符为中心向两侧进行扩展,显然这个复杂度是O(N^2)的,关于字符串的题目常用的算法有KMP、后缀数组、AC 自动机,这道题目利用扩展KMP可以解答,其时间复杂度也很快O(N*logN)。但是,今天笔者介绍一个专门针对回文子串的算法,其时间复杂度为O(n),这就是manacher
算法。
大家都知道,求回文串时需要判断其奇偶性,也就是求aba 和abba 的算法略有差距。然而,这个算法做了一个简单的处理,很巧妙地把奇数长度回文串与偶数长度回文串统一考虑,也就是在每个相邻的字符之间插入一个分隔符,串的首尾也要加,当然这个分隔符不能再原串中出现,一般可以用‘#’或者‘$’等字符。例如:
原串:abaab
新串:#a#b#a#a#b#
这样一来,原来的奇数长度回文串还是奇数长度,偶数长度的也变成以‘#’为中心奇数回文串了。
接下来就是算法的中心思想,用一个辅助数组P 记录以每个字符为中心的最长回文半径,也就是P[i]记录以Str[i]字符为中心的最长回文串半径。P[i]最小为1,此时回文串为Str[i]本身。
我们可以对上述例子写出其P 数组,如下
新串: # a # b # a # a # b #
P[] : 1 2 1 4 1 2 5 2 1 2 1
我们可以证明P[i]-1 就是以Str[i]为中心的回文串在原串当中的长度。
证明:
1、显然L=2*P[i]-1 即为新串中以Str[i]为中心最长回文串长度。
2、以Str[i]为中心的回文串一定是以#开头和结尾的,例如“#b#b#”或“#b#a#b#”所以L 减去最前或者最后的‘#’字符就是原串中长度 的二倍,即原串长度为(L-1)/2,化简的P[i]-1。得证。 依次从前往后求得P 数组就可以了,这里用到了DP(动态规划)的思想,也就是求P[i] 的时候,前面的P[]值已经得到了,我们利用回文串的特殊性质可以进行一个大大的优化。
先把核心代码贴上:
for (i = 0; i < len; i++)
{
if (maxid > i)
{
p[i] = min(p[2*id - i], maxid - i);
}
else
{
p[i] = 1;
}
while (newstr[i+p[i]] == newstr[i-p[i]])
p[i]++;
if (p[i] + i > maxid)
{
maxid = p[i] + i;
id = i;
}
if (ans < p[i])
ans = p[i];
}为了防止求P[i]向两边扩展时可能数组越界,我们需要在数组最前面和最后面加一个特殊字符,令P[0]=‘$’最后位置默认为‘\0’不需要特殊处理。此外,我们用MaxId 变量记录在求i 之前的回文串中,延伸至最右端的位置,同时用id 记录取这个MaxId 的id 值。通过下面这句话,算法避免了很多没必要的重复匹配。if (maxid > i)
{
p[i] = min(p[2*id - i], maxid - i);
}那么这句话是怎么得来的呢,其实就是利用了回文串的对称性,如下图,
j=2*id-1 即为i 关于id 的对称点,根据对称性,P[j]的回文串也是可以对称到i 这边的,但是如果P[j]的回文串对称过来以后超过MaxId 的话,超出部分就不能对称过来了,如下图,

所以这里P[i]为的下限为两者中的较小者,p[i]=Min(p[2*id-i],MaxId-i)。算法的有效比较次数为MaxId 次,所以说这个算法的时间复杂度为O(n)。
具体代码,求解最长回文字符串的代码:
#include <iostream>
#include <algorithm>
#include <string>
#include <cstring>
using namespace std;
const int MAX = 100001;
int len, p[2*MAX];
char str[2*MAX], newstr[2*MAX];
void change()
{
int i;
newstr[0] = '@';
newstr[1] = '#';
for (i = 0; i < len; i++){
newstr[2*i + 2] = str[i];
newstr[2*i + 3] = '#';
}
newstr[2*len + 2] = '\0';
return ;
}
void Manacher()
{
int i, j, id, maxid = 0, ans = 1;
len = 2 * len + 2;
for (i = 0; i < len; i++){
if (maxid > i){
p[i] = min(p[2*id - i], maxid - i);
}
else{
p[i] = 1;
}
while (newstr[i+p[i]] == newstr[i-p[i]])
p[i]++;
if (p[i] + i > maxid){
maxid = p[i] + i;
id = i;
}
if (ans < p[i])
ans = p[i];
}
for (i = id, j = 0; i < id + ans; i++){
if (newstr[i] != '#'){
str[j] = newstr[i];
j++;
}
}
str[id+ans] = '\0';
cout << ans - 1 << " " << str << endl;
return ;
}
int main()
{
while (scanf("%s", &str))
{
if (strcmp(str, "END") == 0) break;
len = strlen(str);
change();
Manacher();
}
return 0;
}
相关文章推荐
- lightoj 1030 Discovering Gold (基础概率dp)
- C语言函数sscanf()的用法
- ECharts实例开发学习笔记二——时间轴
- 金钱观
- HTML5中的表单+Ajax+localStorage+Cookie
- 10_mybatis与Spring的整合
- 算法代码:查找数组中第i小的元素
- HDU - 2844 Coins(多重背包)
- 测试用例知识,总结边界值,因果图,等价类划分法
- 备忘----android环境搭建
- linux常用命令 和shell脚本(必知)
- 关于Java中多个数据excel表格的导出
- 3、下载与安装Eclipse
- java实现链表的反转
- HDU 1238 Substrings(求公共正反向连续子串)
- Scala教程(十)函数与闭包详解
- Java中Collection和Collections的区别
- VS2010/MFC编程之树型控件的创建及CTreeCtrl类的成员函数和实例
- IOS开发基础知识--碎片22
- 3、下载与安装Eclipse
