POJ 2635 The Embarrassed Cryptographer(素数筛+高精度求模+同余模)
2015-07-25 16:52
423 查看
The Embarrassed Cryptographer
Description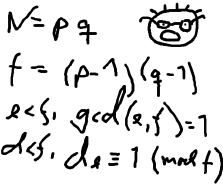 The young and very promising cryptographer Odd Even has implemented the security module of a large system with thousands of users, which is now in use in his company. The cryptographic keys are created from the product of two primes, and are believed to be secure because there is no known method for factoring such a product effectively. What Odd Even did not think of, was that both factors in a key should be large, not just their product. It is now possible that some of the users of the system have weak keys. In a desperate attempt not to be fired, Odd Even secretly goes through all the users keys, to check if they are strong enough. He uses his very poweful Atari, and is especially careful when checking his boss' key.InputThe input consists of no more than 20 test cases. Each test case is a line with the integers 4 <= K <= 10100 and 2 <= L <= 106. K is the key itself, a product of two primes. L is the wanted minimum size of the factors in the key. The input set is terminated by a case where K = 0 and L = 0.OutputFor each number K, if one of its factors are strictly less than the required L, your program should output "BAD p", where p is the smallest factor in K. Otherwise, it should output "GOOD". Cases should be separated by a line-break.Sample Input
The young and very promising cryptographer Odd Even has implemented the security module of a large system with thousands of users, which is now in use in his company. The cryptographic keys are created from the product of two primes, and are believed to be secure because there is no known method for factoring such a product effectively. What Odd Even did not think of, was that both factors in a key should be large, not just their product. It is now possible that some of the users of the system have weak keys. In a desperate attempt not to be fired, Odd Even secretly goes through all the users keys, to check if they are strong enough. He uses his very poweful Atari, and is especially careful when checking his boss' key.InputThe input consists of no more than 20 test cases. Each test case is a line with the integers 4 <= K <= 10100 and 2 <= L <= 106. K is the key itself, a product of two primes. L is the wanted minimum size of the factors in the key. The input set is terminated by a case where K = 0 and L = 0.OutputFor each number K, if one of its factors are strictly less than the required L, your program should output "BAD p", where p is the smallest factor in K. Otherwise, it should output "GOOD". Cases should be separated by a line-break.Sample Input
| Time Limit: 2000MS | Memory Limit: 65536K | |
| Total Submissions: 12906 | Accepted: 3473 |
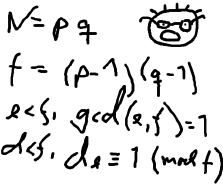 The young and very promising cryptographer Odd Even has implemented the security module of a large system with thousands of users, which is now in use in his company. The cryptographic keys are created from the product of two primes, and are believed to be secure because there is no known method for factoring such a product effectively. What Odd Even did not think of, was that both factors in a key should be large, not just their product. It is now possible that some of the users of the system have weak keys. In a desperate attempt not to be fired, Odd Even secretly goes through all the users keys, to check if they are strong enough. He uses his very poweful Atari, and is especially careful when checking his boss' key.InputThe input consists of no more than 20 test cases. Each test case is a line with the integers 4 <= K <= 10100 and 2 <= L <= 106. K is the key itself, a product of two primes. L is the wanted minimum size of the factors in the key. The input set is terminated by a case where K = 0 and L = 0.OutputFor each number K, if one of its factors are strictly less than the required L, your program should output "BAD p", where p is the smallest factor in K. Otherwise, it should output "GOOD". Cases should be separated by a line-break.Sample Input
The young and very promising cryptographer Odd Even has implemented the security module of a large system with thousands of users, which is now in use in his company. The cryptographic keys are created from the product of two primes, and are believed to be secure because there is no known method for factoring such a product effectively. What Odd Even did not think of, was that both factors in a key should be large, not just their product. It is now possible that some of the users of the system have weak keys. In a desperate attempt not to be fired, Odd Even secretly goes through all the users keys, to check if they are strong enough. He uses his very poweful Atari, and is especially careful when checking his boss' key.InputThe input consists of no more than 20 test cases. Each test case is a line with the integers 4 <= K <= 10100 and 2 <= L <= 106. K is the key itself, a product of two primes. L is the wanted minimum size of the factors in the key. The input set is terminated by a case where K = 0 and L = 0.OutputFor each number K, if one of its factors are strictly less than the required L, your program should output "BAD p", where p is the smallest factor in K. Otherwise, it should output "GOOD". Cases should be separated by a line-break.Sample Input143 10 143 20 667 20 667 30 2573 30 2573 40 0 0Sample Output
GOOD BAD 11 GOOD BAD 23 GOOD BAD 31
给一个非常大的数K,和一个L(2<=L<=10^6)
其中K 是两个素数的乘积,如果这两个素数中的最小值比L大 输出"GOOD" , 否则输出"BAD" + 两个素数中小的那个
可以先将L内的素数全部存起来,来依次判断是否 K%某素数=0
因为K非常大,所以可以把它化成千进制,如12345678 化为 [12][345][678]
判断[12][345][678]%5 是否为0
先判断 12%5=2;
下一步 (345+2*1000)%5=0;
最后 (678+0*1000)%5=3;
所以 12345678 不能整除 5。
#include <iostream>#include <cstdio>#include <stdlib.h>#include <cstring>#include <string>#include <algorithm>#include <cmath>#define N 1000001using namespace std;int su,s;bool u;void sai(){ memset(u,true,sizeof(u)); s=1; for(int i=2; i<N; i++) { if(u[i]) su[s++]=i; for(int j=1; j<s; j++) { if(i*su[j]>N) break; u[i*su[j]]=false; if(i%su[j]==0) break; } }}int a;int main(){ char str[10010]; int n,p; sai(); //素数筛 while(scanf("%s%d",str,&n),n) { int len=strlen(str); int mm=len%3; int aa=0; if(mm==1) //换成千进制 a[aa++] = str[0]-'0'; else if(mm==2) a[aa++] = (int)(str[0]-'0')*10 + (int)(str[1]-'0'); for(int i=mm;i<len;i+=3) a[aa++] = (str[i]-'0')*100 + (str[i+1]-'0')*10 + str[i+2]-'0'; bool flag=false; int mul=1000; for(int i=1;i<s;i++) //依次判断每个素数 { if(su[i]>n) break; int sum=a[0]%su[i]; for(int j=1;j<aa;j++) //是否能整除 { sum = (a[j]+mul*sum)%su[i]; } if(sum==0) { if(su[i]<n) { p=su[i]; flag=true; break; } } } if(flag) printf("BAD %d\n",p); else printf("GOOD\n"); } return 0;}相关文章推荐
- 各种排序算法比较(2):时间复杂度,空间复杂度
- 在ASP.NET MVC中,使用Bundle来打包压缩js和css
- DMA和cache的一致性
- struts2(3)
- WP与IOS与Android的后台机制相同与不同
- Ubuntu修改apt-get镜像地址提高下载速度
- getcher getch getched用法和缓冲区的概念
- 怎样取消已经被内核占用的按键驱动中断号
- android jxl OOM内存溢出问题解决(适用大部分内存溢出)
- javascript解析xml实现省市县三级联动的方法
- 正数的算术平均值不小于几何平均值的一个初等证明
- Kali Linux web渗透测试 学习笔记 1 系统安装
- visual_studio插件开发中的一些问题
- AT89C51特殊功能寄存器速查表
- 各种排序算法比较(1):稳定性
- http form get post本质区别
- 正数的算术平均值不小于几何平均值的一个初等证明
- adt快捷键
- 高流量站点NGINX与PHP-fpm配置优化(译)
- 以太网帧格式详解
