SVD解线性方程组——秘密大起底
2014-07-19 10:21
357 查看
奇异值分解(SVD)是计算机视觉领域中一种使用最为广泛的矩阵分解技术。我们已经知道了一个矩阵A可以分解为下面这样一种形式: A = VDV' (1),这里V是一个正交矩阵(AA' = I),V' 代表V的转置, D是一个对角矩阵, 对角矩阵A中的每一个对角元都是A的特征值。
对于一个方阵A,我们总能找到一种特征值分解的方式,A可以表达为 (1)所示的形式,但当A不是一个方阵时,我们需要知道是否也存在一个相似的分解方法。幸运的是,这样的分解方式是存在的,这就是SVD。
对于任一给定的矩阵A(m * n),都存在这样的分解:A = UDV' 。 这里, U是一个m * m的正交矩阵,D是一个m * n的对角矩阵, V是一个n * n的正交矩阵。
D中的对角元叫做A的奇异值,U中的列向量叫做A的左奇异向量, V中的列向量叫做A的右奇异向量。
由于我们主要讲解如何用SVD解线性方程组,对于SVD的一些性质,我们不再详述,感兴趣的可以参考相关资料。
SVD解优化问题:
(1)解非齐次线性方程组(Ax = b)
我们可以用SVD解诸如 Ax = b 这样的线性方程组。这个问题其实就等价于最小化|| Ax - b ||2 (2),这是一个分线性优化问题。
已经知道svd(A) = UDV',并且对于一个正交矩阵M,满足这样一条性质: || Mv || = || v || (3), v是列向量。把(3)代入(2)中,得到:
min(|| Ax - b ||2) = min(|| UDV' x - b ||) = min(DV' x - U'b) (4)。设y = V'x, b' = U'b,(4)式可重新表述为Dy = b'(D是一个对角矩阵),表达成矩阵的形式如下:
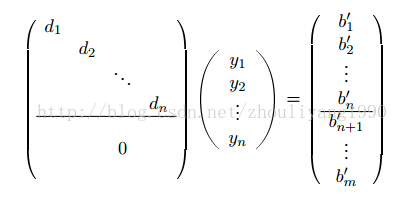
(ps: 如果无法浏览图片,可以访问这个网址https://img-blog.csdn.net/20140719101625906?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvemhvdWxpeWFuZzE5OTA=/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center)
根据上式,方程组的解很容易得到 yi = bi' / di。
(2)解齐次方程组(Ax = 0)
相似的情况,我们把问题转化为最小化|| Ax ||2的非线性优化问题,我们已经知道了x = 0是该方程组的一个特解,为了避免x = 0这种情况(因为在实际的应用中x = 0往往不是我们想要的),我们增加一个约束,比如|| x ||2 = 1,这样,问题就变为:
min(|| Ax ||2) , || x ||2 = 1 或 min(|| Ax ||) , || x || = 1
再次应用(3)式, || Ax || = || UDV' x || = || DV' x||,令y = V'x, 因此,问题变为min(|| Dy ||), || y || = 1。由于D是一个对角矩阵,对角元的元素按递减的顺序排列,因此最优解在y = (0, 0,..., 1)'是取得,又因为x = Vy, 所以最优解就是V的最小奇异值对应的列向量,比如,最小奇异值在第8行8列,那么x = V的第8个列向量。
对于一个方阵A,我们总能找到一种特征值分解的方式,A可以表达为 (1)所示的形式,但当A不是一个方阵时,我们需要知道是否也存在一个相似的分解方法。幸运的是,这样的分解方式是存在的,这就是SVD。
对于任一给定的矩阵A(m * n),都存在这样的分解:A = UDV' 。 这里, U是一个m * m的正交矩阵,D是一个m * n的对角矩阵, V是一个n * n的正交矩阵。
D中的对角元叫做A的奇异值,U中的列向量叫做A的左奇异向量, V中的列向量叫做A的右奇异向量。
由于我们主要讲解如何用SVD解线性方程组,对于SVD的一些性质,我们不再详述,感兴趣的可以参考相关资料。
SVD解优化问题:
(1)解非齐次线性方程组(Ax = b)
我们可以用SVD解诸如 Ax = b 这样的线性方程组。这个问题其实就等价于最小化|| Ax - b ||2 (2),这是一个分线性优化问题。
已经知道svd(A) = UDV',并且对于一个正交矩阵M,满足这样一条性质: || Mv || = || v || (3), v是列向量。把(3)代入(2)中,得到:
min(|| Ax - b ||2) = min(|| UDV' x - b ||) = min(DV' x - U'b) (4)。设y = V'x, b' = U'b,(4)式可重新表述为Dy = b'(D是一个对角矩阵),表达成矩阵的形式如下:
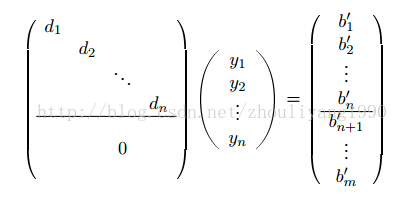
(ps: 如果无法浏览图片,可以访问这个网址https://img-blog.csdn.net/20140719101625906?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvemhvdWxpeWFuZzE5OTA=/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center)
根据上式,方程组的解很容易得到 yi = bi' / di。
(2)解齐次方程组(Ax = 0)
相似的情况,我们把问题转化为最小化|| Ax ||2的非线性优化问题,我们已经知道了x = 0是该方程组的一个特解,为了避免x = 0这种情况(因为在实际的应用中x = 0往往不是我们想要的),我们增加一个约束,比如|| x ||2 = 1,这样,问题就变为:
min(|| Ax ||2) , || x ||2 = 1 或 min(|| Ax ||) , || x || = 1
再次应用(3)式, || Ax || = || UDV' x || = || DV' x||,令y = V'x, 因此,问题变为min(|| Dy ||), || y || = 1。由于D是一个对角矩阵,对角元的元素按递减的顺序排列,因此最优解在y = (0, 0,..., 1)'是取得,又因为x = Vy, 所以最优解就是V的最小奇异值对应的列向量,比如,最小奇异值在第8行8列,那么x = V的第8个列向量。
相关文章推荐
- [数学]线性方程组的解、SVD
- 从iphone6起底中国黄牛行业的秘密
- 求解线性方程组(SVD,QR,Gauss,LU)
- SVD解线性方程组(非齐次)
- 奇异值分解 SVD C++代码
- 探真无阻塞加载javascript脚本技术,我们会发现很多意想不到的秘密
- dig挖出DNS的秘密
- SVD奇异值分解 可视化特征脸
- 网盘秒传的秘密
- Bitmap的秘密
- 1643: [Usaco2007 Oct]Bessie's Secret Pasture 贝茜的秘密草坪
- C#秘密武器之反射——替换反射
- C#秘密武器之异步编程
- SVD奇异值分解
- 关于工资的三个秘密
- 豌豆荚的秘密:一个85后CEO的创业传奇
- 第14章 秘密
- 电脑键盘上你所不知道的秘密,学会了很牛气!
- dig挖出DNS的秘密
- C语言的那些秘密之---函数返回局部变量
