概率论快速学习04:概率公理 全概率 贝叶斯 事件独立性
2014-06-02 10:30
676 查看
原创地址: http://www.cnblogs.com/Alandre/ (泥沙砖瓦浆木匠),需要转载的,保留下! Thanks
加油! 大牛总是不断努力,你却更需要加倍努力.
今天继续概率论:
全概率
贝叶斯
事件独立性
In the Set :




The law of total probability is the proposition that if
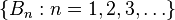
is a finite or countably infinitepartition of a sample space (in other words, a set of pairwise disjoint events whose union is the entire sample space) and each event

is measurable, then for any event

of the same probability space:

example:
例. 甲、乙两家工厂生产某型号车床,其中次品率分别为20%, 5%。已知每月甲厂生产的数量是乙厂的两倍,现从一个月的产品中任意抽检一件,求该件产品为合格的概率?
设A表示产品合格,B表示产品来自甲厂

Bayes
for some partition {Bj} of the event space, the event space is given or conceptualized in terms of P(Bj) and P(A|Bj). It is then useful to compute P(A) using the law of total probability:

example:
An entomologist spots what might be a rare subspecies of beetle, due to the pattern on its back. In the rare subspecies, 98% have the pattern, or P(Pattern|Rare) = 98%. In the common subspecies, 5% have the pattern. The rare subspecies accounts for only 0.1% of the population. How likely is the beetle having the pattern to be rare, or what is P(Rare|Pattern)?
From the extended form of Bayes' theorem (since any beetle can be only rare or common),
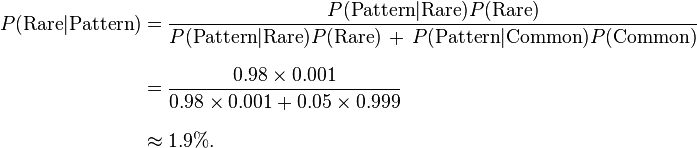
One more example:

Two events A and B are independent if and only if their joint probability equals the product of their probabilities:
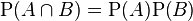
.
Why this defines independence is made clear by rewriting with conditional probabilities:
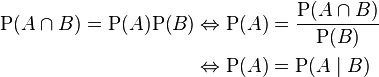
how about Three events

sometimes , we will see the Opposition that can be used to make the mess done. We will use the rule of independence such as :
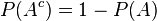
加油! 大牛总是不断努力,你却更需要加倍努力.
Written In The Font
数学和生活是技术之本, 有了数学,加上生活,才会开心.今天继续概率论:
全概率
贝叶斯
事件独立性
Content
The total probabilityIn the Set :




The law of total probability is the proposition that if
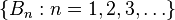
is a finite or countably infinitepartition of a sample space (in other words, a set of pairwise disjoint events whose union is the entire sample space) and each event

is measurable, then for any event

of the same probability space:

example:
例. 甲、乙两家工厂生产某型号车床,其中次品率分别为20%, 5%。已知每月甲厂生产的数量是乙厂的两倍,现从一个月的产品中任意抽检一件,求该件产品为合格的概率?
设A表示产品合格,B表示产品来自甲厂

Bayes
for some partition {Bj} of the event space, the event space is given or conceptualized in terms of P(Bj) and P(A|Bj). It is then useful to compute P(A) using the law of total probability:

example:
An entomologist spots what might be a rare subspecies of beetle, due to the pattern on its back. In the rare subspecies, 98% have the pattern, or P(Pattern|Rare) = 98%. In the common subspecies, 5% have the pattern. The rare subspecies accounts for only 0.1% of the population. How likely is the beetle having the pattern to be rare, or what is P(Rare|Pattern)?
From the extended form of Bayes' theorem (since any beetle can be only rare or common),
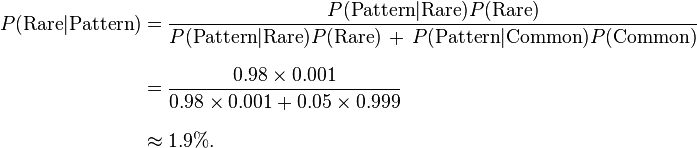
One more example:

Independence
Two eventsTwo events A and B are independent if and only if their joint probability equals the product of their probabilities:
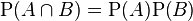
.
Why this defines independence is made clear by rewriting with conditional probabilities:
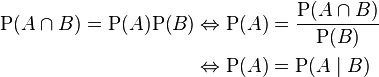
how about Three events

sometimes , we will see the Opposition that can be used to make the mess done. We will use the rule of independence such as :
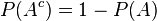
Editor's Note
“学吧,至少不亏.”一句良言 终身受用.相关文章推荐
- 概率论快速学习04:概率公理 全概率 贝叶斯 事件独立性
- 概率论高速学习04:概率公理 全概率 贝叶斯 事件独立性
- 概率论快速学习02:概率公理
- 概率论快速学习03:概率公理补充
- 概率论快速学习02:概率公理
- 概率论快速学习03:概率公理补充
- 【概率论】1.2事件的运算、条件概率和独立性
- 概率论高速学习03:概率公理补充
- 概率论高速学习03:概率公理补充
- OGG学习笔记04-OGG复制部署快速参考
- 概率数理统计-- 1.3 事件的运算、条件概率与独立性
- Khan公开课 - 概率学习笔记(一)独立事件、相依事件和排列组合
- 条件概率与事件的相互独立性
- Python快速学习04:循环 & 函数
- 微信学习_04_关注事件,关键字回复
- Machine Learning in Action 学习笔记-(4)基于概率论的分类方法:朴素贝叶斯
- 浩爷概率DP快速学习方案--让你从5秒真男人中脱颖而出-。-!
- 贝叶斯学习--极大后验概率假设和极大似然假设
- 概率论02 概率公理
- 概率论快速学习01:计数
