LSA学习笔记
2013-11-23 16:53
190 查看
1.LSA简介
LSA(latent semantic analysis)潜在语义分析,也被称为LSI(latent semantic index),是Scott Deerwester, Susan T. Dumais 等人在1990 年提出来的一种新的索引和检索方法。该方法和传统向量空间模型(vector space model)一样使用向量来表示词(terms)和文档(documents),并通过向量间的关系(如夹角)来判断词及文档间的关系;而不同的是,LSA将词和文档映射到潜在语义空间,从而去除了原始向量空间中的一些“噪音”,提高了信息检索的精确度。
2.理论学习
我把LSA的实现分成四个步骤:1)样本组织
2)SVD分解
3)降维
4)在潜在主义空间上查询
具体过程如下:
1)样本组织:
a)读取所有文档中的单词,去除其中无意义的停止词,为每个单词和文档分别设置一个索引号。(停止词:ftp://ftp.cs.cornell.edu/pub/smart/english.stop)
b)创建M x N的Term-Document矩阵,记为矩阵X,其中行表示每一个词,列表示每一个文档。X(i,j)的值为第i个单词在 第j个文档中出现的次数,i,j分别为单词和文档的索引号。
c)计算每个单词的IDF(逆向文件频率)。IDF的主要思想是:如果包含词条t的文档越少,也就是n越小,IDF越大,则说明词条t具有很好的类别区分能力。
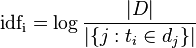
其中|D|为文档总数,
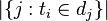
为包含单词
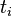
的文档数目。
d)求每个单词的IF*IDF值:X(i,j)=X(i,j)*idfi
2)SVD分解
SVD分解,即矩阵的奇异值分解。对X进行SVD分解::X=TSDT。其中S是一个对角矩阵,对角线上的元素即为X的奇异值。
3)降维
设潜在语义空间的维度为k,则在S中保留X的前k个奇异值,相应的T和D取其间k列。设S*、T*、D*为降维后的矩阵,则T*S*矩阵的行就可以看作是单词在潜在语义空间的坐标,D*S*矩阵的行表示文档在潜在语义空间的坐标。
4)在潜在主义空间上查询
用户输入的检索语句被称为伪文档,因为它也是有多个词汇构成,和文档相似。所以很自然的想法就是将该伪文档转换为文档坐标,然后通过比较该伪文档与每个文档的空间夹角,检索出该伪文档的相关文档。
设Xq为一个查询列向量,Xq(i)为第i个单词在伪文档中出现的次数。则伪文档的文档坐标为:Dq = XqT T S-1中。
Dq计算出来后,就可以通过向量运算迭代比较Dq和文档集合中所有所有文档(D*S*)的cosine夹角,找出相关文档。
3.总结
LSA通过SVD分解获得单词和文档在潜在语义空间上的坐标,并解决了一义多词的问题。相关文章推荐
- 动易2006序列号破解算法公布
- C#数据结构与算法揭秘二
- 浅析STL中的常用算法
- JavaScript 组件之旅(二)编码实现和算法
- 将15位身份证补全为18位身份证的算法示例详解
- C++算法系列之日历生成的算法代码
- 1 2 3 4 5 6 7 8 9 = 110的java实现
- Sedgewick之巨著《算法》,与高德纳TAOCP一脉相承
- 【代码】Pythonの代码片段
- STL中算法
- 数据结构&算法学习
- 算法的时间复杂度
- 算法导论:选择排序的原理与实现
- PHP实现四种常用的排序算法
- 图解插入排序算法
- 一些常见算法的JavaScript实现
- 平方根sqrt()函数的底层算法效率
- 二叉搜索树的一些相关算法介绍
- 欧几里德算法(辗转相处法)练手
- 面试中常见的一些算法问题
