欧拉函数
2013-04-14 00:57
387 查看
欧拉函数直接计算公式
欧拉函数的定义: E(N)= ( 区间[1,N-1] 中与 N 互质的整数个数).
对于 积性函数 F(X*Y),当且仅当 GCD(X,Y)= 1 时, F(X*Y) = F(X)* F(Y)
任意整数可因式分解为如下形式:
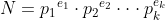
其中( p1, p2 ... pk 为质数, ei 为次数 )
所以
%20=%20E(p_%7B1%7D%5E%7Be_%7Bi%7D%7D%20*%20p_%7B2%7D%5E%7Be_%7B2%7D%7D%20*%20...%20*%20p_%7Bk%7D%5E%7Be_%7Bk%7D%7D%20))
因为 欧拉函数 E(X)为积性函数, 所以
=%20E(p_%7B1%7D%5E%7Be_%7Bi%7D%7D%20)%20*%20E(p_%7B2%7D%5E%7Be_%7B2%7D%7D%20)*%20...%20*%20E(p_%7Bk%7D%5E%7Be_%7Bk%7D%7D%20))
对于
)
, 我们知道 因为pi 为质数,所以 [ 1, pi-1 ] 区间的数都与 pi 互质
对于 区间[ 1,
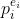
] ,共有
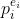
个数,
因为
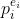
只有一个质因子,
所以与
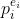
约数大于1 的必定包含 质因子
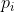
, 其数量为
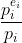
所以
%20=%20p_%7Bi%7D%5E%7Be_%7Bi%7D%7D%20-%20%5Cfrac%7Bp_%7Bi%7D%5E%7Be_%7Bi%7D%7D%7D%7B%20p_%7Bi%7D%7D)
又 E(N)为积性函数,所以可得 :
%20=%20%5Cprod_%7Bi=1%7D%5E%7Bk%7D%20(%20p_%7Bi%7D%5E%7Be_%7Bi%7D%7D-p_%7Bi%7D%5E%7Be_%7Bi%7D-1%7D%20)%20=%20%5Cprod_%7Bi=1%7D%5E%7Bk%7D%20(%20(p_%7Bi%7D-1)*p_%7Bi%7D%5E%7Be_%7Bi%7D-1%7D%20))
又因为
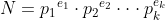
其中( p1, p2 ... pk 为质数, ei 为次数 )
%20=%20N*%5Cprod_%7Bi=1%7D%5E%7Bk%7D%20(%20%5Cfrac%7B%20p_i-1%20%7D%7Bp_i%7D))
但是此计算公式,除法过多,所以计算速度较慢
在程序中利用欧拉函数如下性质,可以快速求出欧拉函数的值 ( P为N的质因子 )
若(N%P==0 && (N/P)%P==0) 则有:E(N)=E(N/P)*P;
若(N%P==0 && (N/P)%P!=0) 则有:E(N)=E(N/P)*(P-1);
直接计算欧拉函数值代码:
关于欧拉函数其他的证明方式:
证明过程如下:
1. 容易想到:当n为素数时,PHI(n) = n - 1。因为每个比n小的正整数都和n互素。
当n为素数p的k次方时,PHI(n) = p ^ k - p ^ (k - 1)。因为在1到n之间的正整数只有p的倍数和n不互素,这样的数有(p ^ k / p)个。
2. 如果m和n互素,即GCD(m, n) = 1,那么PHI(m * n) = PHI(m) * PHI(n)。
用中国剩余定理可以证明,证明的思路是建立这样一种一一对应的关系(a, b) <-> x,其中正整数a小于m并且gcd(a, m) = 1,正整数b小于n并且gcd(b, n) = 1,正整数x小于m*n并且gcd(m*n, x) = 1。证明过程如下:
1)根据中国剩余定理,如果m和n互素,那么关于未知量x的方程组x % m = a, x % n = b(0 <= a < m, 0 <= b < n),当0 <= x < m * n时存在并且仅存在一个解。容易证明,如果两个这样的方程组有相同的m, n但是a, b不同,那么他们的解x一定不同。
2)首先用反正法证明:gcd(m, a) = 1且gcd(n, b) = 1是gcd(m*n, x) = 1的必要条件:假设gcd(a, m) = k > 1,由此可得:a = a' * k; m = m' * k => x = k' * m + a = k' * k * m' + k * a' = k * (k' * m'
+ a'); 所以gcd(x, m) = k > 1。同理可证,如果gcd(b, n) > 1, 那么gcd(x, n) > 1。所以x和m * n互素的必要条件是a和m互诉且b和n互素。
3)接下来我们证明充分性:由x % m = a 可以得到x = k * m + a;由欧几里德算法求最大公约数的过程(就不证明了,呵呵,还得想)可以知道gcd(x, m) = gcd(m, a) = 1;同理可得,如果gcd(n, b) = 1那么gcd(x, n) = 1。接下来很容易得到:gcd(m*n, x) = 1。从而证明了充分性。
4)上面三步的结论表明,数对(a, b)是可以和x建立起一一对应的关系的,所以有多少个不同的(a, b),就有多少个不同的x。
3.将n分解成素数乘积后,显然对于任意的i, j(i != j)都满足 pi ^ ki和pj ^ kj是互素的,于是可以的到上面的公式。
使用素因子性质预处理出欧拉函数代码:
用递推的方法来实现欧拉函数
欧拉函数可以很方便的计算小于某个数N但N互质的数的个数,
即M(1<=M<N)且gcd(M, N)=1, M的个数很容易由欧拉函数来计算出来.
欧拉函数的表达式为 E(N)= N*(1-1/f_1)*(1-1/f_2)*(1-1/f_3)....依次类推,
其中f_1, f_2, f_3等是N的不相同的质因子.
例如 12=2*2*3 那么12有两个不同的质因子2, 3,
由欧拉函数可得小于12但与12互质的个数为
12*(1-1/2)(1-1/3)=4,
列举为1, 5, 7, 11.
那么在实际实现欧拉函数的时候, 可以把一个数进行质因子分解, 依次代入欧拉函数进行求解. 我们今天介绍一种用欧拉函数自身的递推关系来实现的方法.
首先介绍这种递推关系, 假设数N有m个不相同的质因子f_1, f_2,f_3....f_m.
那么数(N/f_1)有多少个不同的质因子呢?
分成两种情况来考虑,
第一种情况, N只包含一个f_1因子, 那么N/f_1有m-1个因子f_2,f_3,...,f_m.
我们考察N/f_1和N的欧拉函数形式E(N) = N*(1-1/f_1)*(1-1/f_2)*(1-1/f_3)*...*(1-1/f_m) E(N/f_1) = N/f_1*(1-1/f_2)*(1-1/f_3)*...*(1-1/f_m). 把(1-1/f_1)化为(f_1
- 1)/f_1则可以显然看到E(N) = (f_1 - 1)*E(N/f_1).
第二种情况, N包含一个以上的f_1因子, 那么N/f_1包含了与N相同的质因子个数且此时两者的欧拉函数分别记为
E(N) = N*(1-1/f_1)*(1-1/f_2)*(1-1/f_3)*...*(1-1/f_m)
E(N/f_1) = N/f_1*(1-1/f_1)*(1-1/f_2)*(1-1/f_3)*...*(1-1/f_m).
这个递推关系更明显了E(N) = (f_1)*E(N/f_1).
因此这两种递推关系只与质因子f_1有关, 而f_1可以是N的任意一个质因子.
用代码来实现时可以取N的最小质因子来简化实现过程.
在实际代码过程可以和搜索质数的"筛子法"相结合, 因为"筛子法"相当于优先找到了每个数的最小质因子.
欧拉函数的定义: E(N)= ( 区间[1,N-1] 中与 N 互质的整数个数).
对于 积性函数 F(X*Y),当且仅当 GCD(X,Y)= 1 时, F(X*Y) = F(X)* F(Y)
任意整数可因式分解为如下形式:
其中( p1, p2 ... pk 为质数, ei 为次数 )
所以
因为 欧拉函数 E(X)为积性函数, 所以
对于
, 我们知道 因为pi 为质数,所以 [ 1, pi-1 ] 区间的数都与 pi 互质
对于 区间[ 1,
] ,共有
个数,
因为
只有一个质因子,
所以与
约数大于1 的必定包含 质因子
, 其数量为
所以
又 E(N)为积性函数,所以可得 :
又因为
其中( p1, p2 ... pk 为质数, ei 为次数 )
但是此计算公式,除法过多,所以计算速度较慢
在程序中利用欧拉函数如下性质,可以快速求出欧拉函数的值 ( P为N的质因子 )
若(N%P==0 && (N/P)%P==0) 则有:E(N)=E(N/P)*P;
若(N%P==0 && (N/P)%P!=0) 则有:E(N)=E(N/P)*(P-1);
直接计算欧拉函数值代码:
View Code
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<math.h>
typedef long long LL;
LL Eular( LL x )
{
if( x == 0 ) return 0;
LL res = 1, t = x;
for(LL i = 2; i <= (LL)sqrt(1.*x); i++)
{
if( t%i == 0 )
{
res *= (i-1);
t /= i;
while( t%i ==0 )
{
res *= i;
t /= i;
}
}
if( t == 1 ) break;
}
if( t > 1 ) { res *= (t-1); }
return res;
}
int main()
{
LL x;
while( scanf("%lld", &x) != EOF)
printf("%lld\n", Eular(x) );
return 0;
}关于欧拉函数其他的证明方式:
证明过程如下:
1. 容易想到:当n为素数时,PHI(n) = n - 1。因为每个比n小的正整数都和n互素。
当n为素数p的k次方时,PHI(n) = p ^ k - p ^ (k - 1)。因为在1到n之间的正整数只有p的倍数和n不互素,这样的数有(p ^ k / p)个。
2. 如果m和n互素,即GCD(m, n) = 1,那么PHI(m * n) = PHI(m) * PHI(n)。
用中国剩余定理可以证明,证明的思路是建立这样一种一一对应的关系(a, b) <-> x,其中正整数a小于m并且gcd(a, m) = 1,正整数b小于n并且gcd(b, n) = 1,正整数x小于m*n并且gcd(m*n, x) = 1。证明过程如下:
1)根据中国剩余定理,如果m和n互素,那么关于未知量x的方程组x % m = a, x % n = b(0 <= a < m, 0 <= b < n),当0 <= x < m * n时存在并且仅存在一个解。容易证明,如果两个这样的方程组有相同的m, n但是a, b不同,那么他们的解x一定不同。
2)首先用反正法证明:gcd(m, a) = 1且gcd(n, b) = 1是gcd(m*n, x) = 1的必要条件:假设gcd(a, m) = k > 1,由此可得:a = a' * k; m = m' * k => x = k' * m + a = k' * k * m' + k * a' = k * (k' * m'
+ a'); 所以gcd(x, m) = k > 1。同理可证,如果gcd(b, n) > 1, 那么gcd(x, n) > 1。所以x和m * n互素的必要条件是a和m互诉且b和n互素。
3)接下来我们证明充分性:由x % m = a 可以得到x = k * m + a;由欧几里德算法求最大公约数的过程(就不证明了,呵呵,还得想)可以知道gcd(x, m) = gcd(m, a) = 1;同理可得,如果gcd(n, b) = 1那么gcd(x, n) = 1。接下来很容易得到:gcd(m*n, x) = 1。从而证明了充分性。
4)上面三步的结论表明,数对(a, b)是可以和x建立起一一对应的关系的,所以有多少个不同的(a, b),就有多少个不同的x。
3.将n分解成素数乘积后,显然对于任意的i, j(i != j)都满足 pi ^ ki和pj ^ kj是互素的,于是可以的到上面的公式。
使用素因子性质预处理出欧拉函数代码:
View Code
跟据上面的公式,可以得到关于欧拉函数的递推关系:
假设素数p能整除n,那么
如果p还能整除n / p, PHI(n) = PHI(n / p) * p;
如果p不能整除n / p, PHI(n) = PHI(n / p) * (p - 1);
下面的程序是求1到10000之间所有整数的欧拉函数:
char mark[10000] = {0};
int prime[1230];
int size = 0;
int phi[10000];
int main () {
int i, j;
/*筛法求素数*/
for (i = 2; i < 10000; i++) {
if (!mark[i]) prime[size++] = i;
for (j = 0; j < size && prime[j] * i < 10000; j++) {
mark[prime[j] * i] = 1;
if (i % prime[j] == 0) break;
}
}
/*求欧拉函数*/
phi[1] = 1;
for (i = 2; i < 10000; i++) {
if (!mark[i]) {
phi[i] = i - 1;
continue;
}
for (j = 0; j < size && prime[j] * prime[j] <= i; j++) {
if (i % prime[j] == 0) {
if (i / prime[j] % prime[j] == 0)
phi[i] = prime[j] * phi[i / prime[j]];
else
phi[i] = (prime[j] - 1) * phi[i / prime[j]];
break;
}
}
}
return 0;
}
从别人那里学到的对求欧拉函数部分的优化,使每个数的欧拉函数只由它的最小素因子求出:
phi[1] = 1;
for (i = 1; i < 10000; i++) {
for (j = 0; j < size && prime[j] * i <= 10000; j++) {
if (i % prime[j] == 0) {
phi[prime[j] * i] = prime[j] * phi[i];
break;
}
else {
phi[prime[j] * i] = phi[i] * (prime[j] - 1);
}
}
}用递推的方法来实现欧拉函数
欧拉函数可以很方便的计算小于某个数N但N互质的数的个数,
即M(1<=M<N)且gcd(M, N)=1, M的个数很容易由欧拉函数来计算出来.
欧拉函数的表达式为 E(N)= N*(1-1/f_1)*(1-1/f_2)*(1-1/f_3)....依次类推,
其中f_1, f_2, f_3等是N的不相同的质因子.
例如 12=2*2*3 那么12有两个不同的质因子2, 3,
由欧拉函数可得小于12但与12互质的个数为
12*(1-1/2)(1-1/3)=4,
列举为1, 5, 7, 11.
那么在实际实现欧拉函数的时候, 可以把一个数进行质因子分解, 依次代入欧拉函数进行求解. 我们今天介绍一种用欧拉函数自身的递推关系来实现的方法.
首先介绍这种递推关系, 假设数N有m个不相同的质因子f_1, f_2,f_3....f_m.
那么数(N/f_1)有多少个不同的质因子呢?
分成两种情况来考虑,
第一种情况, N只包含一个f_1因子, 那么N/f_1有m-1个因子f_2,f_3,...,f_m.
我们考察N/f_1和N的欧拉函数形式E(N) = N*(1-1/f_1)*(1-1/f_2)*(1-1/f_3)*...*(1-1/f_m) E(N/f_1) = N/f_1*(1-1/f_2)*(1-1/f_3)*...*(1-1/f_m). 把(1-1/f_1)化为(f_1
- 1)/f_1则可以显然看到E(N) = (f_1 - 1)*E(N/f_1).
第二种情况, N包含一个以上的f_1因子, 那么N/f_1包含了与N相同的质因子个数且此时两者的欧拉函数分别记为
E(N) = N*(1-1/f_1)*(1-1/f_2)*(1-1/f_3)*...*(1-1/f_m)
E(N/f_1) = N/f_1*(1-1/f_1)*(1-1/f_2)*(1-1/f_3)*...*(1-1/f_m).
这个递推关系更明显了E(N) = (f_1)*E(N/f_1).
因此这两种递推关系只与质因子f_1有关, 而f_1可以是N的任意一个质因子.
用代码来实现时可以取N的最小质因子来简化实现过程.
在实际代码过程可以和搜索质数的"筛子法"相结合, 因为"筛子法"相当于优先找到了每个数的最小质因子.
View Code
const int size = 1000001;
int factor[size]; //factor
记录了n的最小质因子
bool visited[size];
int phy[size]; //phy
记录了与n互质且小于n的个数.
void getPrime()
{
memset(factor, -1, sizeof(factor));
memset(visited, false, sizeof(visited));
for (int i=2; i<size; i++)
{
if (visited[i])
{
//////////////////////////这部分是递归关系的实现//////////////////////////////
int k = i/factor[i];
if (k%factor[i] == 0)
{
phy[i] = phy[k]*factor[i];
}else{
phy[i] = phy[k]*(factor[i] - 1);
}
//////////////////////////////////////////////////////////////////////////////////////////
continue;
}
phy[i] = i -1; //i本身是质数, 与i互质的个数为i-1.
for (int j=i+i; j<size; j+=i)
{
visited[j] = true;
if (factor[j] == -1)
{
factor[j] = i; //用i筛的过程, 就找到了每个以i为最小质因子的数.
}
}
}
相关文章推荐
- 线性时间 筛素数,求前n个数的欧拉函数值,求前n个数的约数个数
- pku1284(求原根,欧拉函数)
- 3696 The Luckiest number 最小X整数倍数 大整数质因数分解及欧拉函数,dfs求大整数的所有约数
- 2478 Farey Sequence //欧拉函数
- poj 2478【线性筛素数+欧拉函数】
- poj 2773 Happy 2006——欧拉函数
- 欧拉函数
- 1089. Farey Sequence (欧拉函数+筛法)
- 欧拉函数
- HDU 3501 Calculation 2 (欧拉函数||容斥原理)
- hdu2824 The Euler function 欧拉函数模板题
- HDU4335 What is N? [数论(欧拉函数)]
- poj2407 欧拉函数
- HDU 1787 简单的求欧拉函数 POJ 2047 裸欧拉函数
- hdu1787GCD Again<欧拉函数>
- 筛选法求欧拉函数phi
- 欧拉函数
- POJ2154——Color(Polya定理+筛素数+欧拉函数)
- hdu 3501(欧拉函数的应用)
- hdu 2824 The Eule Function 筛式欧拉函数
