Python 查找算法_众里寻他千百度,蓦然回首那人却在灯火阑珊处(线性、二分,分块、插值查找算法)
查找算法是用来检索
序列数据(群体)中是否存在给定的数据(
关键字),常用查找算法有:
- 线性查找:
线性查找
也称为顺序查找,用于在无序数列
中查找。 - 二分查找:
二分查找
也称为折半查找
,其算法用于有序数列
。 - 插值查找:
插值查找
是对二分查找
算法的改进。 - 分块查找: 又称为
索引顺序查找
,它是线性查找
的改进版本。 - 树表查找:
树表查找
又可分二叉查找树
、平衡二叉树
查找。 - 哈希查找:
哈希查找
可以直接通过关键字查找到所需要数据。
因
树表查找、
哈希查找的所需篇幅较多,就不在本文讲解。本文将详细介绍除
树表、
哈希之外的查找算法,并分析每一种算法的优点和缺点,并提出相应的优化方案。
1. 线性查找
线性查找也称为
顺序查找,
线性查找属于原始、穷举、暴力查找算法。容易理解、编码实现也简单。但是在数据量较多时,因其算法思想是朴素、穷举的,算法中没有太多优化设计,性能会很低下。
线性查找思想:
- 从头至尾逐一扫描原始列表中的每一个数据,并和给定的关键字进行比较。
- 如果比较相等,则查找成功。
- 当扫描结束后,仍然没有找到与给定关键字相等的数据,则宣布查找失败。
根据
线性查找算法的描述,很容易编码实现:
'''
线性查找算法
参数:
nums: 序列
key:关键字
返回值:
关键字在序列中的位置
如果没有,则返回 -1
'''
def line_find(nums, key):
for i in range(len(nums)):
if nums[i] == key:
return i
return -1
'''
测试线性算法
'''
if __name__ == "__main__":
nums = [4, 1, 8, 10, 3, 5]
key = int(input("请输入要查找的关键字:"))
pos = line_find(nums, key)
print("关键字 {0} 在数列的第 {1} 位置".format(key, pos))
'''
输出结果:
请输入要查找的关键字:3
关键字 3 在数列的 4 位置
'''
线性查找算法的平均时间复杂度分析。
运气最好的情况:如果要查找的关键字恰好在数列的第
1
个位置,则只需要查找 1 次就可以了。如在数列=
[4,1,8,10,3,5]
中查找关键字4
。只需要查找
1
次。运气最不好的情况:一至扫描到数列最尾部时,才找到关键字。
如在数列=
[4,1,8,10,3,5]
中查找是否存在关键字5
。则需要查找的次数等于数列的长度,此处即为
6
次。运气不好不坏:如果要查找的关键字在数列的中间某个位置,则查找的概率是
1/n
。n
为数列长度。
线性查找的平均查找次数应该=
(1+n)/2。换成大
O表示法则为
O(n)。
大
O表示法中忽视常量。
线性查找最糟糕情况是:扫描完整个数列后,没有所要查找的关键字。
如在数列=
[4,1,8,10,3,5]中查找是否存在关键字12。扫描了
6次后,铩羽而归!!
改良线性查找算法
可以对
线性查找算法进行相应的优化。如设置“前哨站”。所谓“前哨站”,就是把要查找的关键字在查找之前插入到数列的尾部。
def line_find_(nums, key):
i = 0
while nums[i] != key:
i += 1
return -1 if i == len(nums)-1 else i
'''
测试线性算法
'''
if __name__ == "__main__":
nums = [4, 1, 8, 10, 3, 5]
key = int(input("请输入要查找的关键字:"))
# 查找之前,先把关键字存储到列到的尾部
nums.append(key)
pos = line_find_(nums, key)
print("关键字 {0} 在数列的第 {1} 位置".format(key, pos))
用"前哨站"优化后的线性查找算法的时间复杂度没有变化,O(n)。或者说从
2者代码上看,也没有太多变化。
但从代码的实际运行角度而言,第
2种方案减少了
if指令的次数,同样减少了编译后的指令,也就减少了
CPU执行指令的次数,这种优化属于微优化,不是算法本质上的优化。
使用计算机编程语言所编写的代码为伪指令代码。
经过编译后的指令代码叫
CPU指令集。有一种优化方案就是减少编译后的指令集。
2. 二分查找
二分查找属于
有序查找,所谓
有序查找,指被查找的数列必须是有序的。如在数列=
[4,1,8,10,3,5,12]中查找是否存在关键字
4,因数列不是有序的,所以不能使用
二分查找,如果要使用
二分查找算法,则需要先对数列进行排序。
二分查找使用了
二分(折半)算法思想,
二分查找算法中有
2个关键信息需要随时获取:
- 一个是数列的中间位置
mid_pos
。 - 一个是数列的中间值
mid_val
。
现在通过在数列
nums=[1,3,4,5,8,10,12]中查找关键字
8来了解
二分查找的算法流程。
在进行
二分查找之前,先定义
2个位置(指针)变量:
- 左指针
l_idx
初始指向数列的最左边数字。 - 右指针
r_idx
初始指向数列的最右边数字。
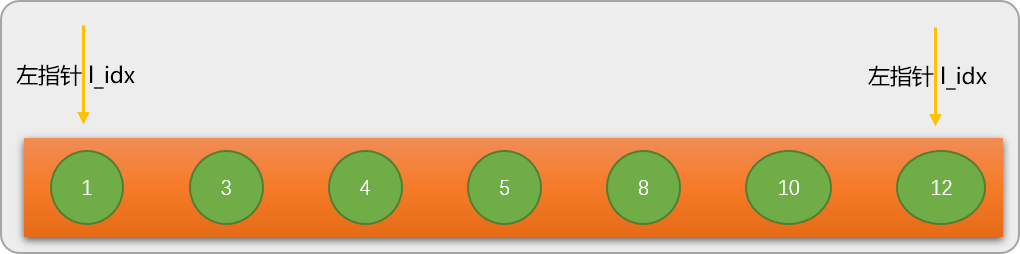
**第
1步:**通过左、右指针的当前位置计算出数列的中间位置
mid_pos=3,并根据
mid_pos的值找出数列中间位置所对应的值
mid_val=nums[mid_pos]是
5。
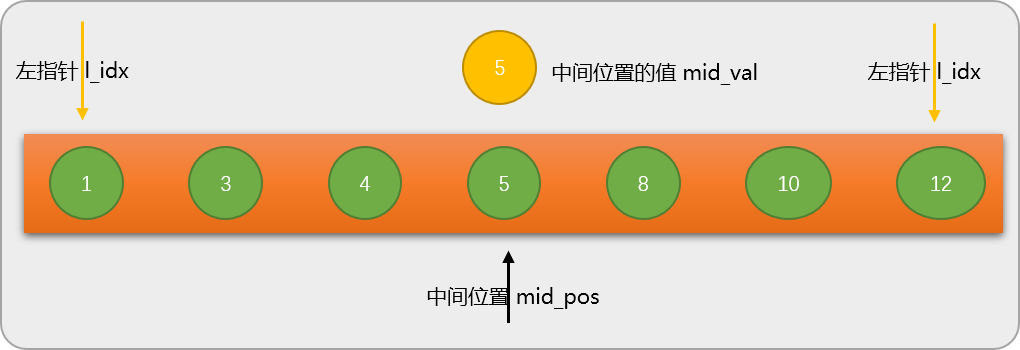
二分查找算法的核心就是要找出数列中间位置的值。
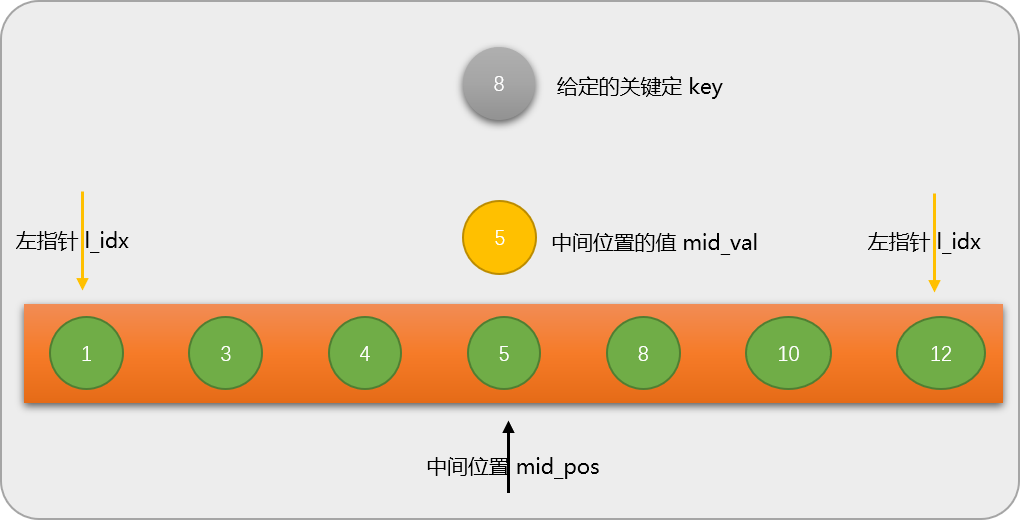
**第
2步:**把数列中间位置的值和给定的关键字相比较。这里关键字是
8,中间位置的值是
5,显然
8是大于
5,因为数列是有序的,自然会想到没有必要再与数列中
5之前的数字比较,而是专心和
5之后的数字比较。
一次比较后再次查找的数列范围缩小了一半。这也是二分算法的由来。
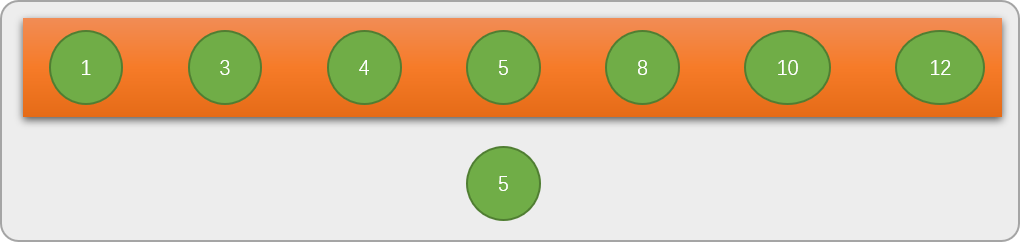
第 3
步:根据比较结果,调整数列的大小,这里的大小调整不是物理结构上调整,而是逻辑上调整,调整后原数列没有变化。也就是通过修改左指针或右指针的位置,从逻辑上改变数列大小。调整后的数列如下图。
二分查找算法中数列的范围由左指针到右指针的长度决定。

第 4 步:重复上述步骤,至到找到或找不到为止。
编码实现二分查找算法
''' 二分查找算法 ''' def binary_find(nums, key): # 初始左指针 l_idx = 0 # 初始在指针 r_ldx = len(nums) - 1 while l_idx <= r_ldx: # 计算出中间位置 mid_pos = (r_ldx + l_idx) // 2 # 计算中间位置的值 mid_val = nums[mid_pos] # 与关键字比较 if mid_val == key: # 出口一:比较相等,有此关键字,返回关键字所在位置 return mid_pos elif mid_val > key: # 说明查找范围应该缩少在原数的左边 r_ldx = mid_pos - 1 else: l_idx = mid_pos + 1 # 出口二:没有查找到给定关键字 return -1 ''' 测试二分查找 ''' if __name__ == "__main__": nums = [1, 3, 4, 5, 8, 10, 12] key = 3 pos = binary_find(nums, key) print(pos)
通过前面对
二分算法流程的分析,可知
二分查找的
子问题和
原始问题是同一个逻辑,所以可以使用递归实现:
''' 递归实现二分查找 ''' def binary_find_dg(nums, key, l_idx, r_ldx): if l_idx > r_ldx: # 出口一:没有查找到给定关键字 return -1 # 计算出中间位置 mid_pos = (r_ldx + l_idx) // 2 # 计算中间位置的值 mid_val = nums[mid_pos] # 与关键字比较 if mid_val == key: # 出口二:比较相等,有此关键字,返回关键字所在位置 return mid_pos elif mid_val > key: # 说明查找范围应该缩少在原数的左边 r_ldx = mid_pos - 1 else: l_idx = mid_pos + 1 return binary_find_dg(nums, key, l_idx, r_ldx) ''' 测试二分查找 ''' if __name__ == "__main__": nums = [1, 3, 4, 5, 8, 10, 12] key = 8 pos = binary_find_dg(nums, key,0,len(nums)-1) print(pos)
二分查找性能分析:
二分查找的过程用树形结构描述会更直观,当搜索完毕后,绘制出来树结构是一棵二叉树。
- 如上述代码执行过程中,先找到数列中的中间数字
5
,然后以5
为根节点构建唯一结点树。
5
和关键字8
比较后,再在以数字5
为分界线的右边数列中找到中间数字10
,树形结构会变成下图所示。
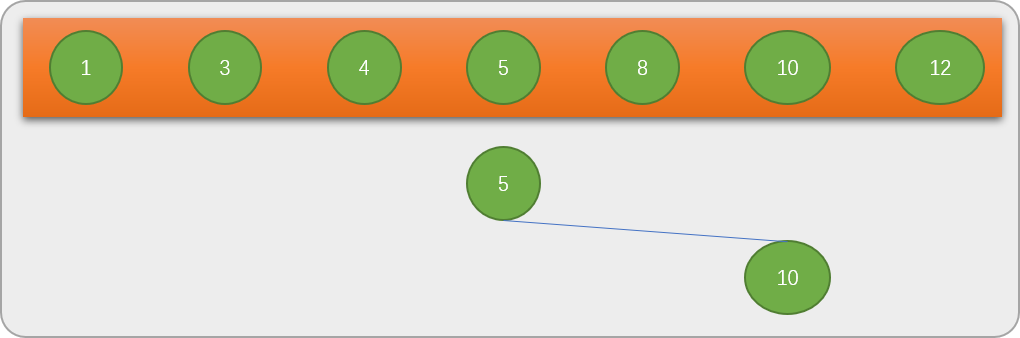
10
和关键字8
比较后,再在10
的左边查找。
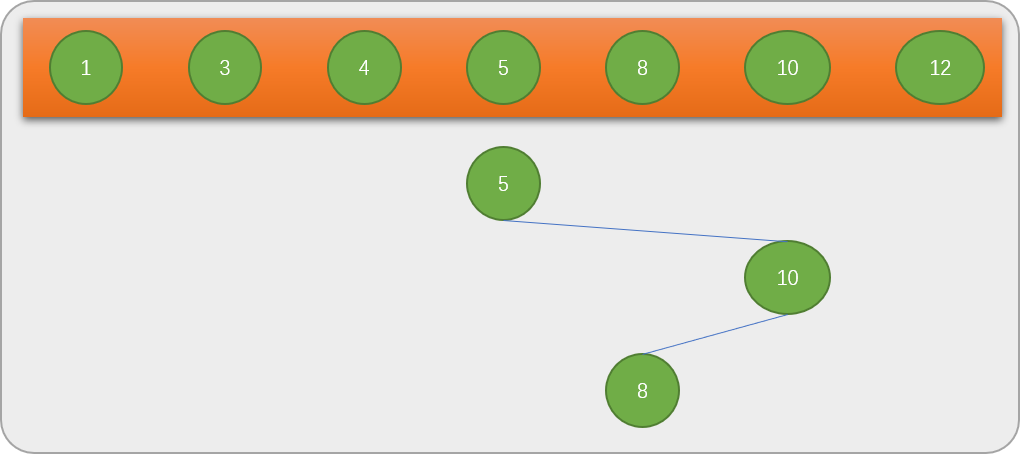
查找到
8后,意味着二分查找已经找到结果,只需要
3次就能查找到最终结果。
从二叉树的结构上可以直观得到结论:二分查找关键字的次数由关键字在二叉树结构中的深度决定。
- 上述是查找给定的数字
8
,为了能查找到数列中的任意一个数字,最终完整的树结构应该如下图所示。
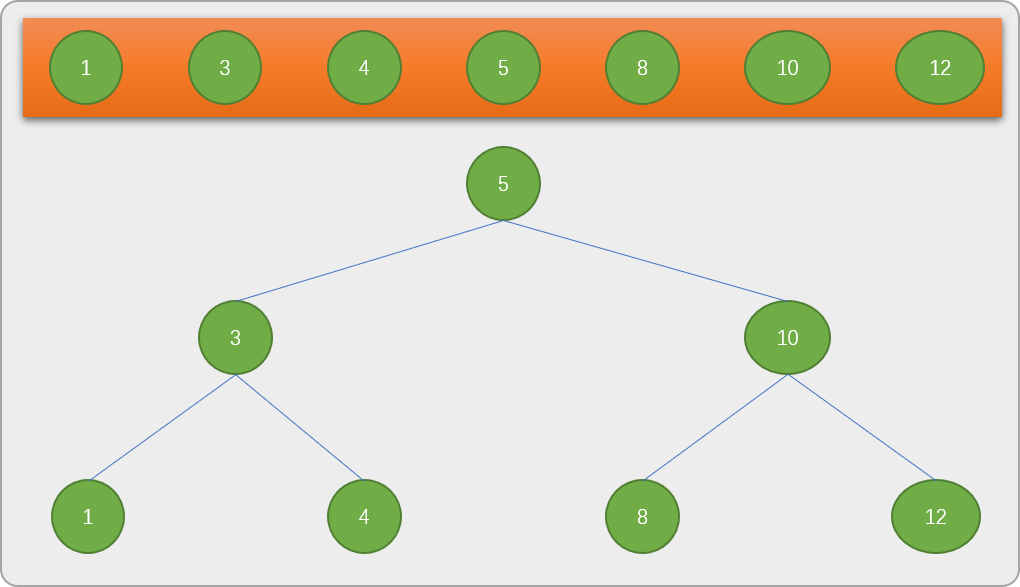
很明显,树结构是标准的二叉树。从树结构上可以看出,无论查找任何数字,最小是
1次,如查找数字
5,最多也只需要
3次,比线性查找要快很多。
根据二叉树的特性,结点个数为
n的树的深度为 h=log2(n+1),所以二分查找算法的大
O表示的时间复杂度为
O(logn),是对数级别的时间度。
当对长度为
1000的数列进行二分查找时,所需次数最多只要
10次,
二分查找算法的效率显然是高效的。
但是,
二分查找需要对数列提前排序,前面的时间复杂度是没有考虑排序时间的。所以,二分查找一般适合数字变化稳定的有序数列。
3. 插值查找
插值查找本质是
二分查找,
插值查找对
二分查找算法中查找中间位置的计算逻辑进行了改进。
原生
二分查找算法中计算中间位置的逻辑:中间位置等于左指针位置加上右指针位置然后除以
2。
# 计算中间位置 mid_pos = (r_ldx + l_idx) // 2
插值算法计算中间位置逻辑如下所示:
key为要查找的关键字!!
# 插值算法中计算中间位置 mid_pos = l_idx + (key - nums[l_idx]) // (nums[r_idx] - nums[l_idx]) * (r_idx - l_idx)
编码实现插值查找:
# 插值查找基于二分法,只是mid计算方法不同
def binary_search(nums, key):
l_idx = 0
r_idx = len(nums) - 1
old_mid = -1
mid_pos = None
while l_idx < r_idx and nums[0] <= key and nums[r_idx] >= key and old_mid != mid_pos:
# 中间位置计算
mid_pos = l_idx + (key - nums[l_idx]) // (nums[r_idx] - nums[l_idx]) * (r_idx - l_idx)
old_mid = mid_pos
if nums[mid_pos] == key:
return "index is {}, target value is {}".format(mid_pos, nums[mid_pos])
# 此时目标值在中间值右边,更新左边界位置
elif nums[mid_pos] < key:
l_idx = mid_pos + 1
# 此时目标值在中间值左边,更新右边界位置
elif nums[mid_pos] > key:
r_idx = mid_pos - 1
return "Not find"
li =[1, 3, 4, 5, 8, 10, 12]
print(binary_search(li, 6))
插值算法的中间位置计算时,对中间位置的计算有可能多次计算的结果是一样的,此时可以认为查找失败。
插值算法的性能介于线性查找和二分查找之间。
当数列中数字较多且分布又比较均匀时,插值查找算法的平均性能比折半查找要好的多。如果数列中数据分布非常不均匀,此种情况下插值算法并不是最好的选择。
4. 分块查找
分块查找类似于数据库中的
索引查询,所以
分块查找也称为
索引查找。其算法的核心还是线性查找。
现有原始数列
nums=[5,1,9,11,23,16,12,18,24,32,29,25],需要查找关键字
11是否存在。
**第
1步:**使用
分块查找之前,先要对原始数列按区域分成多个块。至于分成多少块,可根据实际情况自行定义。分块时有一个要求,前一个块中的
最大值必须小于后一个块的
最小值。
块内部无序,但要保持整个数列
按块有序。
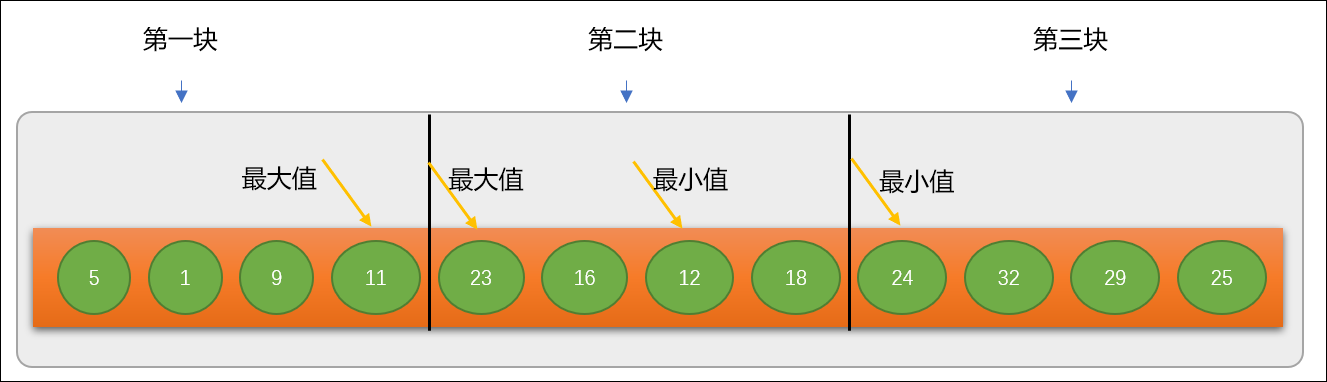
分块查找要求原始数列从整体上具有升序或降序趋势,如果数列的分布不具有趋向性,如果仍然想使用分块查找,则需要进行分块有序调整。
**第
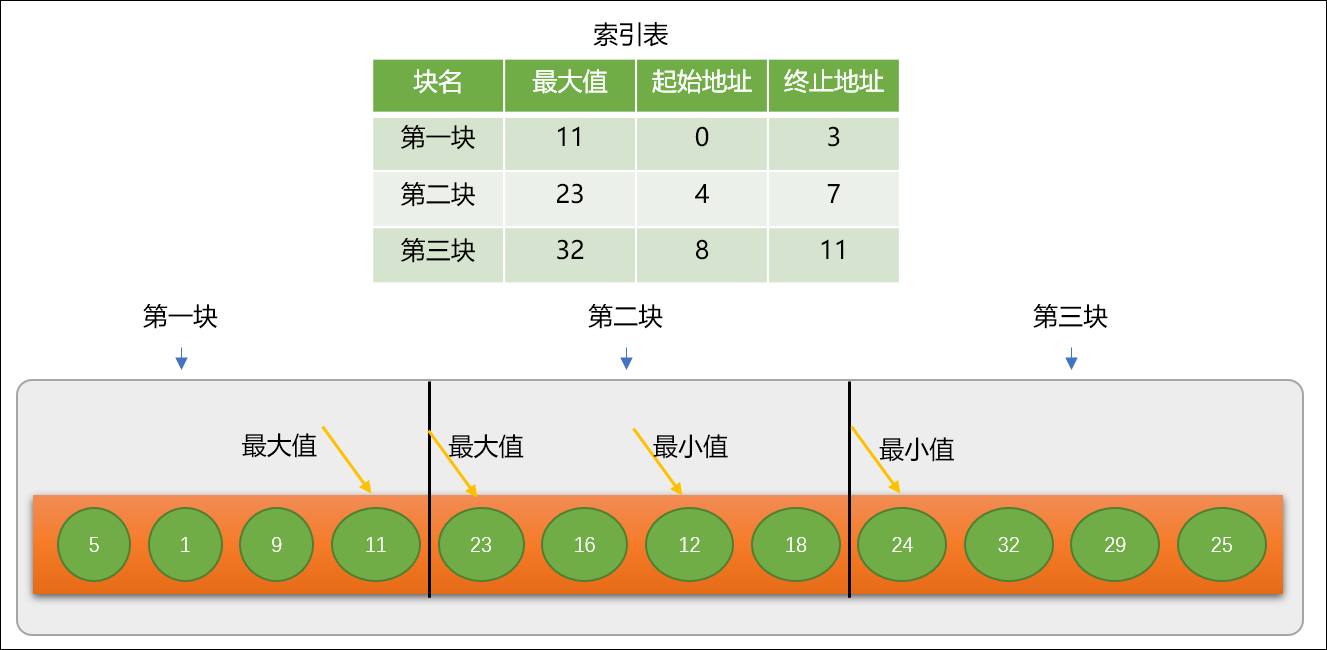
2步:**根据分块信息,建立
索引表。
索引表至少应该有
2个字段,每一块中的
最大值数字以及每一块的
起始地址。显然
索引表中的数字是有序的。
**第
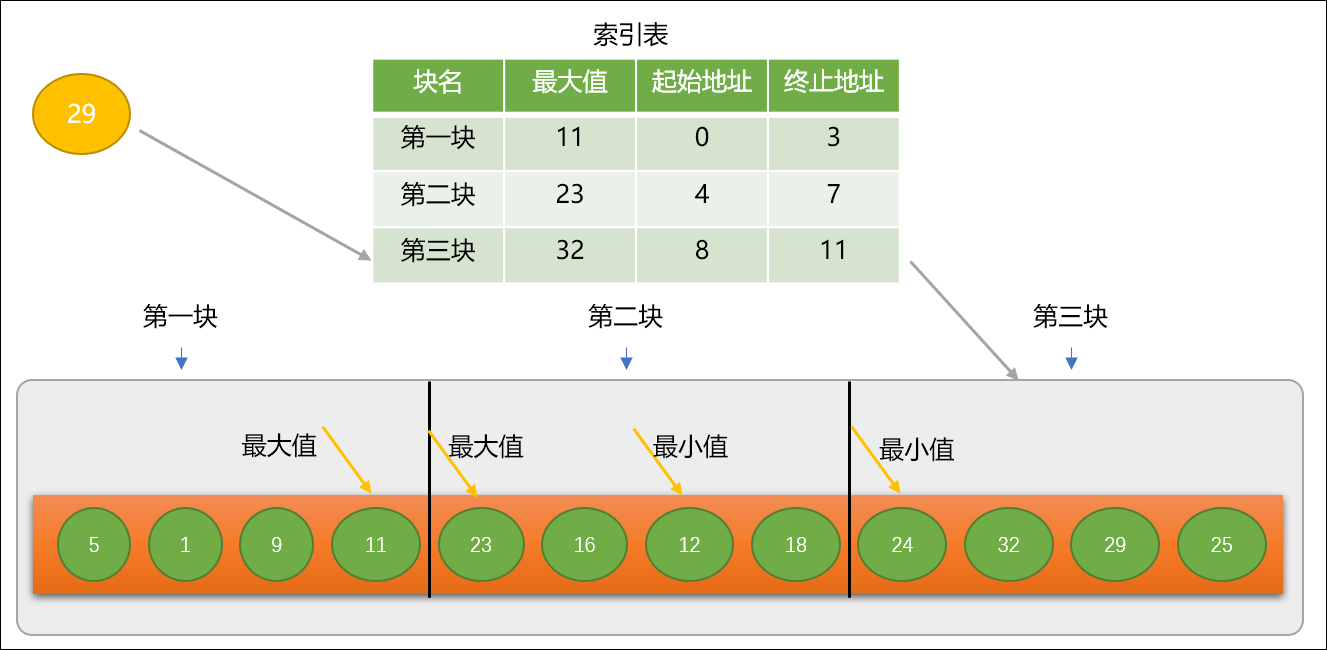
3步:**查找给定关键字时,先查找
索引表,查询关键字应该在那个块中。如查询关键字
29,可知应该在第三块中,然后根据
索引表中所提供的第三块的地址信息,再进入第三块数列,按线性匹配算法查找
29具体位置。
编码实现分块查找:
先编码实现根据分块数量、创建索引表,这里使用
二维列表保存储索引表中的信息。
''' 分块:建立索引表 参数: nums 原始数列 blocks 块大小 ''' def create_index_table(nums, blocks): # 索引表使用列表保存 index_table = [] # 每一块的数量 n = len(nums) // blocks for i in range(0, len(nums), n): # 索引表中的每一行记录 tmp_lst = [] # 最大值 tmp_lst.append(max(nums[i:i + n-1])) # 起始地址 tmp_lst.append(i) # 终止地址 tmp_lst.append(i + n - 1) # 添加到索引表中 index_table.append(tmp_lst) return index_table ''' 测试分块 ''' nums = [5, 1, 9, 11, 23, 16, 12, 18, 24, 32, 29, 25] it = create_index_table(nums, 3) print(it) ''' 输出结果: [[11, 0, 3], [23, 4, 7], [32, 8, 11]] '''
代码执行后,输出结果和分析的结果一样。
以上代码仅对整体趋势有序的数列进行分块。如果整体不是趋向有序,则需要提供相应块排序方案,有兴趣者自行完成。
如上代码仅为说明分块查找算法。
分块查找的完整代码:
'''
分块:建立索引表
参数:
nums 原始数列
blocks 块大小
'''
def create_index_table(nums, blocks):
# 索引表使用列表保存
index_table = []
# 每一块的数量
n = len(nums) // blocks
for i in range(0, len(nums), n):
tmp_lst = []
tmp_lst.append(max(nums[i:i + n - 1]))
tmp_lst.append(i)
tmp_lst.append(i + n - 1)
index_table.append(tmp_lst)
return index_table
'''
使用线性查找算法在对应的块中查找
'''
def lind_find(nums, start, end):
for i in range(start, end):
if key == nums[i]:
return i
break
return -1
'''
测试分块
'''
nums = [5, 1, 9, 11, 23, 16, 12, 18, 24, 32, 29, 25]
key = 16
# 索引表
it = create_index_table(nums, 3)
# 索引表的记录编号
pos = -1
# 在索引表中查询
for n in range(len(it) - 1):
# 是不是在第一块中
if key <= it[0][0]:
pos = 0
# 其它块中
if it
[0] < key <= it[n + 1][0]:
pos = n + 1
break
if pos == -1:
print("{0} 在 {1} 数列中不存在".format(key, nums))
else:
idx = lind_find(nums, it[pos][1], it[pos][2] + 1)
if idx != -1:
print("{0} 在 {1} 数列的 {2} 位置".format(key, nums, idx))
else:
print("{0} 在 {1} 数列中不存在".format(key, nums))
'''
输出结果
16 在 [5, 1, 9, 11, 23, 16, 12, 18, 24, 32, 29, 25] 数列的第 5 位置
'''
分块查找对于整体趋向有序的数列,其查找性能较好。但如果原始数列整体不是有序,则需要提供
块排序算法,时间复杂度没有二分查找算法好。
分块查找需要建立
索引表,这也需要额外的存储空间,其空间复杂度较高。其优于二分的地方在于只需要对原始数列进行部分排序。本质还是以线性查找为主。
5. 总结
本文讲解了
线性、
二分、
插值、
分块查找算法。除此之外,还有其它如
树表查找、
哈希查找等算法。
分块算法可认为是对
线性查找算法的优化。
插值查找可认为是在二分算法基础上的一个变化。
算法没有固定模式,如果学会了
二分查找算法,则认为是学会了一招,需要学会领悟,然后再在这一招上演变出更多变化。
- 常用查找算法(顺序、二分、插值、分块、斐波那契)
- [Python与图像处理]Python实现图像插值(最近邻、双线性、双立方(Bell分布))
- 蓦然回首,机会就在灯火阑珊处
- 查找算法:二分查找(python)
- 查找算法学习总结之顺序、二分、插值查找
- 众里寻他千百度,蓦然回首,那人却在灯火阑珊处
- 众里寻 Bug 千百度,蓦然回首,它却在隔壁老张处……
- 【年度总结】蓦然回首,我在灯火阑珊处
- HUDSON邮件模板问题 <众里寻他千百度,蓦然回首,那‘人’却在灯火阑珊处>
- python实现静态列表二分查找与插值查找
- 蓦然回首,那人却在灯火阑珊处----如何读入多行带空格的字符串
- python 图像插值 最近邻、双线性、双三次
- 众里寻他千百度,蓦然回首,那人却在灯火阑珊处
- 奋斗吧,程序员——第十三章 蓦然回首,那人却在灯火阑珊处
- Python实现分段线性插值
- 转载:HUDSON邮件模板问题 <众里寻他千百度,蓦然回首,那‘人’却在灯火阑珊处>
- 纵里寻她千百度,暮然回首,那人却在灯火阑珊处(微信三方登陆)
- 查找算法(2):线性结构的二分查找
- 三种静态查找算法:顺序、二分/折半、索引/分块查找
- 蓦然回首,那些命令都在灯火阑珊处
