数模学习(二)---Topsis法
一 概述
Topsis法(逼近理想排序法)是系统工程中一种多目标决策方法,找出有限方案中的最优与最劣的方案,当某个可行解方案最靠近最优方案同时又远离最劣方案时,这个方案解的向量集就是最优影响评价指标。
Topsis法其作为一种综合指标的评价方法,区别于如模糊综合评判法,层次分析法,它的主观性比较强,不需要目标函数,也不需要通过相应的检验,即限制要求大大降低,这使它的适用范围更为广泛
二 Topsis影响力度算法步骤
2.1统一指标类型(一般正向化指标)
2.1.1 常见的四种指标总结
| 指标名称 | 指标特征 | 例子 |
|---|---|---|
| 极大型指标(利益型指标) | 越大(多)越好 | 成绩、收益 |
| 极小型指标(成本型指标) | 越小(少)越好 | 成本、污染程度、费用 |
| 中间型指标 | 中间值最好 | 水污染的pH值(最好是pH=7) |
| 区间型指标 | 特定区间内最好 | 疫情期间你的温度、水中营养物的含量 |
因为各指标之间的评价指标不一样,所以我们需要对各个指标进行指标正向化(现在通常是全部转化为极大型指标进行评价)
接下来分别介绍各个指标正向化的步骤
2.1.2 其他指标的指标正向化
①极小型指标—>极大化指标
运用公式:xi(更新值)=max−xix_{i}(更新值) =max-x_{i}xi(更新值)=max−xi1
栗子:
| 姓名 | 成绩 | 吵架次数 | 极小型后的吵架次数 |
|---|---|---|---|
| 小明 | 98 | 4 | 0 |
| 小李 | 86 | 3 | 1 |
| 小红 | 61 | 0 | 4 |
| 小蓝 | 77 | 1 | 3 |
这个可以理解为我需要让他们的量化标准相同,所以脾气越好的个人加分越多,在选择方案时也需要按照相同的量化标准来进行评分2
②中间型指标—>极大型指标
运用公式:
M=max{∣xi−xbest∣}x^i=1−∣xi−xbest∣MM=max\lbrace\vert x_{i}-x_{best}\vert\rbrace\\ \hat x_{i}=1-\frac{\vert x_{i}-x_{best}\vert}{M}
M=max{∣xi−xbest∣}x^i=1−M∣xi−xbest∣
栗子:
| pH值(原) | pH值(更改后) |
|---|---|
| 7 | 1-∣7−7∣2=1\frac{\vert7-7\vert}{2}=12∣7−7∣=1 |
| 6 | 1-∣6−7∣2=12\frac{\vert6-7\vert}{2}=\frac{1}{2}2∣6−7∣=21 |
| 8 | 1-∣8−7∣2=12\frac{\vert8-7\vert}{2}=\frac{1}{2}2∣8−7∣=21 |
| 9 | 1-∣9−7∣2=0\frac{\vert9-7\vert}{2}=02∣9−7∣=0 |
其中M=max{∣7−7∣,∣6−7∣,∣8−7∣,∣9−7∣}=2M=max\lbrace \vert7-7\vert,\vert6-7\vert,\vert8-7\vert,\vert9-7\vert\rbrace=2M=max{∣7−7∣,∣6−7∣,∣8−7∣,∣9−7∣}=2
这样将最好的值xbestx_{best}xbest设为了1,而最差的值为0.将所有的值缩放到了[0,1][0,1][0,1]区间中
③区间型指标—>极大型指标
运用公式:
M=max{∣xmin−xi∣,∣xi−xmax∣}xi={1−a−xiM xi<a1a≤xi≤b1−xi−bMxi>bM=max\lbrace\vert x_{min}-x_{i}\vert,\vert x_{i}-x_{max}\vert\rbrace \\x_{i}=\left\{
\begin{aligned}
1-\frac{a-x_{i}}{M}\ x_{i}<a \\
1\qquad a\leq x_{i}\leq b \\
1-\frac{x_{i}-b}{M}\quad x_{i}>b
\end{aligned}
\right.
M=max{∣xmin−xi∣,∣xi−xmax∣}xi=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧1−Ma−xi xi<a1a≤xi≤b1−Mxi−bxi>b
栗子:(设人体温度最健康的区间是在[36.0,37.0][36.0,37.0][36.0,37.0])
| 温度(原) | 温度(正向化指标) |
|---|---|
| 35.2 | 0.4286 |
| 35.8 | 0.8571 |
| 36.2 | 1 |
| 37.1 | 0.9286 |
| 38.4 | 0 |
其中a=36b=37M=max{∣36−35.2∣,∣38.4−37∣}=1.4a=36 \quad b=37 \\ M=max\lbrace\vert 36-35.2\vert,\vert38.4-37\vert\rbrace=1.4a=36b=37M=max{∣36−35.2∣,∣38.4−37∣}=1.4
2.2 正向化矩阵标准化
目的: 消除不同指标量纲的影响
假设有nnn个对象,mmm个指标,其经过正向化后的矩阵表示如下:
(x11x12...x1mx21x22...x2m............xn1xn2...xnm)那么,其标准化后的矩阵记为Z,Z中的每一个元素,都需要进行:zij=xij∑i=1nxij2即,(每一个元素/其所在列求和后开平方的值) \left( %左括号
\begin{array}{cccc} %该矩阵一共3列,每一列都居中放置
x_{11} & x_{12} & ... & x_{1m}\\ %第一行元素
x_{21} & x_{22} & ... & x_{2m}\\ %第二行元素
... & ... & ... & ...\\ %第二行元素
x_{n1} & x_{n2} & ... & x_{nm}
\end{array}
\right)
\\
那么,其标准化后的矩阵记为Z,Z中的每一个元素,都需要进行:\\
z_{ij}=\frac{x_{ij}}{\sqrt{\sum\limits_{i=1}^nx_{ij}^2}} \\
即,(每一个元素/其所在列求和后开平方的值)⎝⎜⎜⎛x11x21...xn1x12x22...xn2............x1mx2m...xnm⎠⎟⎟⎞那么,其标准化后的矩阵记为Z,Z中的每一个元素,都需要进行:zij=i=1∑nxij2xij即,(每一个元素/其所在列求和后开平方的值)
注意:标准化的方法有很多,没有必要局限于这一个,只要都能达到消除量纲的影响的结果就行
计算得分并归一化
Step1
由上述得到的ZZZ矩阵,进而得到最优向量Zj+=max1≤i≤m∣Zij∣Z_{j}^+ =\mathop{max}\limits_{{1\leq i\leq m}}\vert Z_{ij}\vertZj+=1≤i≤mmax∣Zij∣和最劣向量Zj−=min1≤i≤m∣Zij∣Z_{j}^-=\mathop{min}\limits_{1\leq i \leq m}\vert Z_{ij}\vertZj−=1≤i≤mmin∣Zij∣
Step2
计算所选取或构建的每个指标和最优向量的欧氏距离D+=∑j=1n(Zij−Zj+)2D^+ = \sqrt{\sum\limits_{j=1}^n(Z_{ij}-Z_{j}^+)^2}D+=j=1∑n(Zij−Zj+)2和最劣向量的距离D−=∑j=1n(Zij−Zj−)2D^-=\sqrt{\sum\limits_{j=1}^n(Z_{ij}-Z_{j}^-)^2}D−=j=1∑n(Zij−Zj−)2
Step3
最后得到与最优值的相对接近程度Wi=Di−Di++Di−W_{i}=\frac{D_{i}^-}{D_{i}^++D_{i}^-}Wi=Di++Di−Di−
2.3 Topsis总算法流程
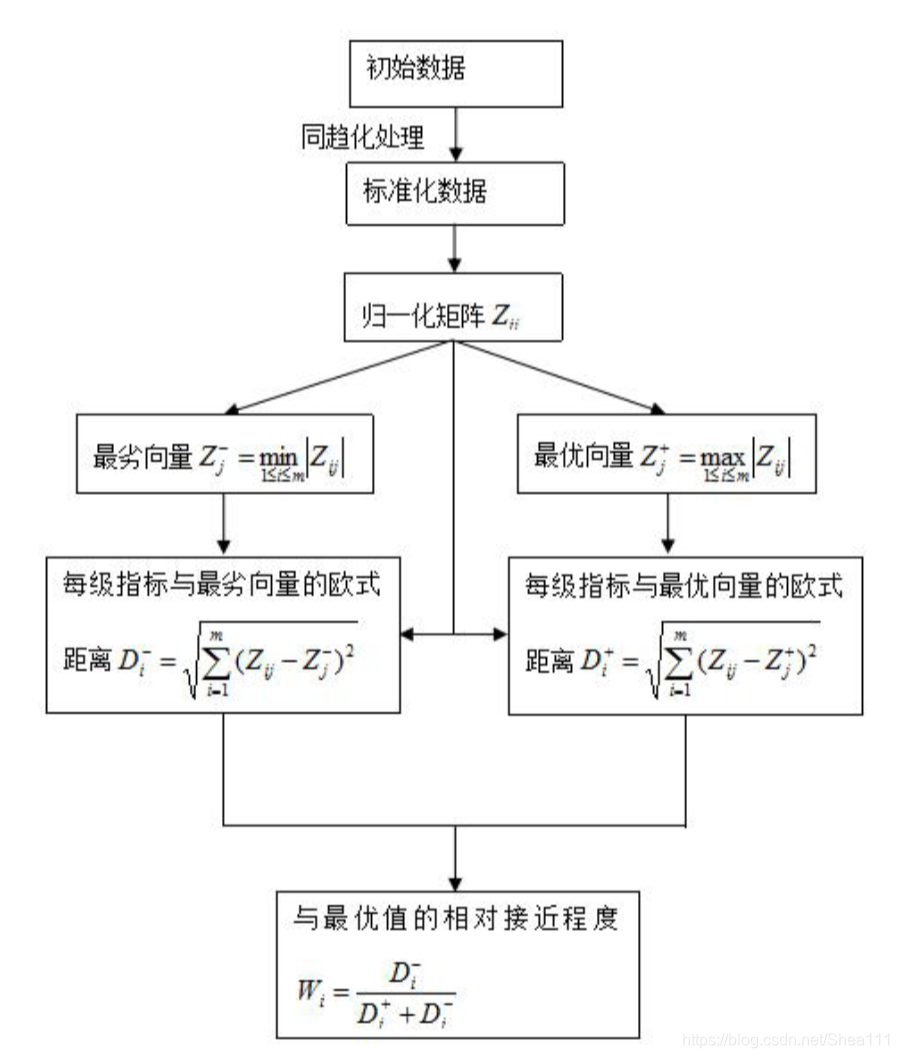
三 部分说明
现实问题中对于这些评价指标的重要性会有一系列的判断说明,跟上篇博客AHP相关,我们可以通过层次分析法来判断各个指标的重要性程度,仅需满足
∑wi=1
\sum w_{i} = 1
∑wi=1
因为层次分析法存在着主观赋值的成分,一般推荐用熵权法作为修正,但是目前我还没有学习,所以先不提这个,之后修改博客的时候会引入链接哒~
- R学习之统计实验(六)--生日问题(R语言编程)-----数模
- R学习之统计实验(九)--和的偶数概率问题(R语言编程)-----数模
- R学习之统计算法与R优化包(极大似然估计练习) --(R语言编程)-----数模
- R学习之统计实验(三)--报童问题(R语言编程)-----数模
- matlab学习之蒙特卡罗 --渡口模型和赶火车问题(matlab编程)-----数模
- 数模电学习之二极管
- R学习之统计实验(四)--电梯问题(R语言编程)-----数模
- R学习之统计实验(七)--大于1问题(R语言编程)-----数模
- R学习之统计算法与R优化包(二分法) --(R语言编程)-----数模
- 数模学习(八)--- 图论最短路径问题
- 【数模学习】Matlab 符号微积分 计算微分、雅可比矩阵、不定积分与定积分、求解微分方程
- R学习之统计实验(二)--掷色子问题(R语言编程)-----数模
- R学习之统计实验(十)--新乒乓问题(R语言编程)-----数模
- R学习之统计算法与R优化包(极大似然估计) --(R语言编程)-----数模
- 数模学习(五)---相关系数
- R学习之统计实验(八)--统计次数概率问题(R语言编程)-----数模
- R学习之统计实验(一)--电梯问题(R语言编程)-----数模
- matlab学习之优化模型 --(matlab编程)-----数模
- R学习之统计实验(五)--赶火车问题(R语言编程)-----数模
- R学习之蒙特卡罗积分 --(R语言编程)-----数模
