Surface Normal Data Guided Depth Recovery with Graph Laplacian Regularization --论文分享
论文分享(1)
0.摘要
近年来,高质量深度图信息越来越多地应用在多媒体应用中。由于深度传感器以及传感技术的限制,事实上,获得的深度图经常为低分辨率的,而且有很多的空洞。在这篇论文中,我们受3D场景的表面法线和3D场景与摄像机距离的几何关系启发,发现法线图可以为深度图的重建提供更多的空间几何约束。因为深度图是一种携带空间信息的特殊图像,所以我们称深度图为2.5D图像。为了探究这个特性,我们提出了一个原创的表面法线数据引导的深度补全的方法,这个方法用表面法线数据和观测到的深度图来估计缺失的深度值和应该插入的深度值。而且,为了保持深度图分段光滑的特性,图像拉普拉斯先验被应用于深度图恢复的逆问题的正则化,一种图像拉普拉斯正则器(GLR) 被提出。(这一段刚开始读有疑问,存疑)最后,这种空间几何约束和图像拉普拉斯正则化被整合进一个统一的优化框架,这个优化框架可以用共轭梯度法(CG)进行有效的求解。和最好的方法进行了大量的定性和定量的评估测试,显示了我们方法的有效性和优越性。
1.介绍
深度图的每个像素记录了3D场景里的物体到摄像机的物理距离。随着传感技术的发展,一个场景中的深度信息现在可以被便宜的摄像机准确地获取,例如tof相机和Microsoft Kinect相机。这个促进了深度图像在现实中的多媒体中的应用,例如3DTV、VR、以及机器人等等。然而,获得的深度图会经历各种各样的退化,导致图像的质量不高。因此,提出一种有效的深度恢复方法来处理各种各样的深度退化是一项重要的工作,这也能更好地支持深度图在多媒体中的应用。

图1:使用结构不一致的图像对重建深度
我们将x定义为底层的高分辨率深度图的向量形式,y定义为获得的低分率深度图,退化模型可以定义成如下:
y = Hx + n (1)
其中,H代表模糊和采样的操作,n代表附加的噪声。从y复原到x是一个病态问题,它要求额外的信息来实现稳定的表现。传统深度图超分辨的方法聚焦于融合多个低分辨率的深度图来获得高分辨率的深度图。有的人提出用贝叶斯来融合获得相似的结果。这些方法都是基于场景是静态的假设。也有人提出了一种基于各向异性全广义变分(TGV)的深度上采样模型,该模型将深度上采样定义为一个高阶正则项的凸优化问题。还有人提出了一种基于交替导引的加权最小二乘法的快速导引插补算法。其实,不看参考文献,这段话根本没有意义。
另一个热门研究方向是融合颜色和深度信息,以提高恢复深度图的精度。有人提出了彩色图引导的深度恢复框架基于自动回归模型,其中一个双边核被使用在彩色图中来保持局部图像框架的形状信息。有人提出了一个鲁棒优化框架采用一个鲁棒罚函数对彩图引导的深度恢复的光滑项进行建模。也有人提出一个联合的优化框架,其中包括AR模型,TV模型,以及LN模型。这些方法取得了明显的效果,并证明了彩色图在深度图恢复中可以扮演一个有效的引导角色。特别是,当上采样因子特别大时,彩色图的纹路在深度图恢复中扮演了更加有利的角色,尤其是与不连续的低分辨率深度图比起来。然而,引导图和深度图在纹路上的不一致,在边界处仍然会导致错误的重建结果。一个例子正如图一所示。RGB-D图像对经常有不一致的结构,彩图的不连续与深度图的不连续并不一致,这都提高了深度图从RGB-D图像对恢复的难度。为了解决这个问题,有人提出了共享信息,参考图像等概念。
最近,表面法线图已经成熟地应用于深度估计。有人采用了深度学习框架来估计表面法线。有人采用表面法线方向分类器来设计深度恢复约束。这些方法不能直接应用于超分辨任务中,因为常规地表面法线数据边界模糊,需要对边界进行更多的约束。
在这篇论文中,受到3D场景表面法线和它们与摄像机间距离的几何关系的启发,我们提出了一个新的深度算子融合了深度信息和对应3D场景估计的表面法线信息。我们也使用了加权图像拉普拉斯正则器来保持深度图的分段光滑特性。实验结果显示我们的方法取得了更好的结果。
2.方法
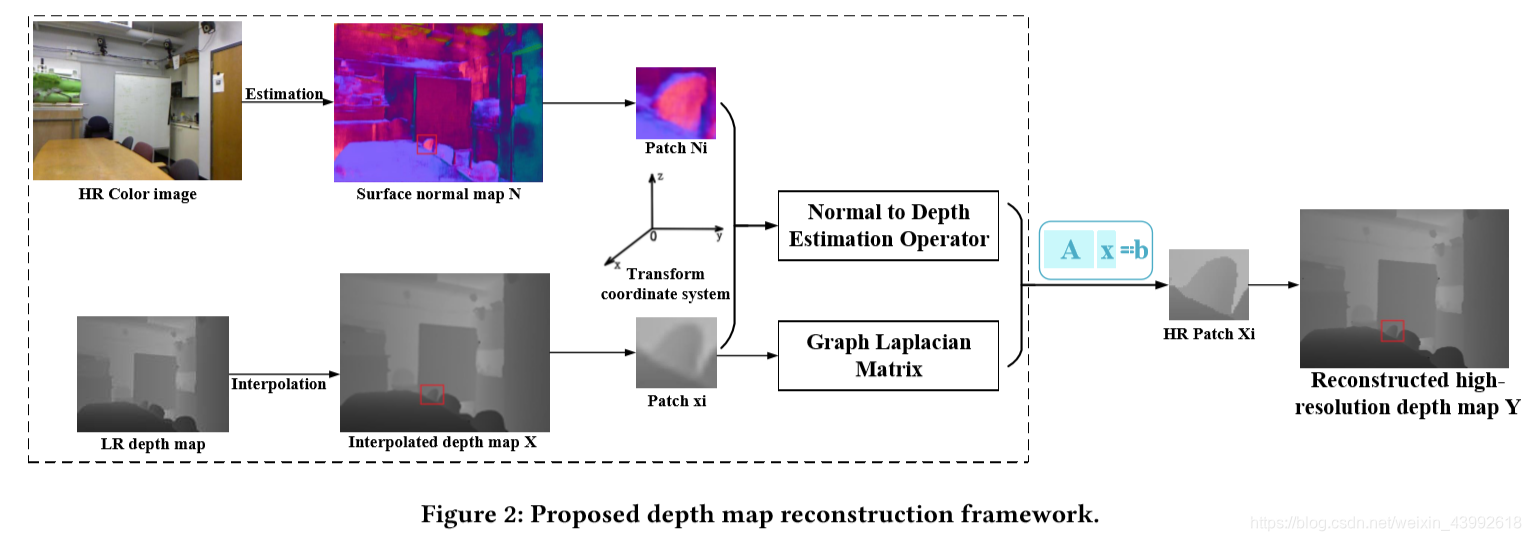
在我们的工作中,我们利用了深度图和它法线图的几何关系来细化深度图,同时一个图像拉普拉斯先验被作为一个有效的正则项来进行添加。提出的深度恢复方法的框架如图二所示,其中包含了三个部分:构建表面法线基于深度估计算子、构建图像拉普拉斯矩阵,通过一个线性系统重建深度图。
2.1 使用表面法线进行深度估计
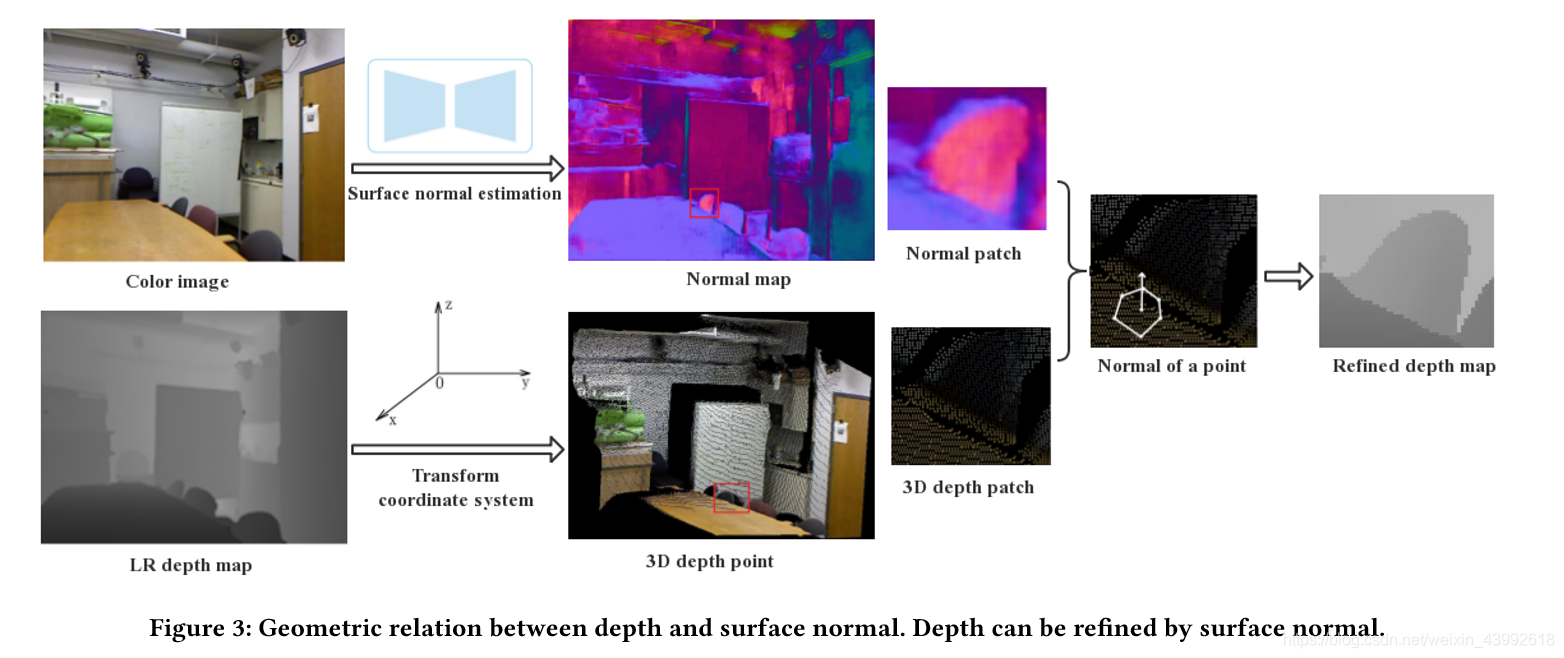
大量的文献已经证明了深度和它表面法线有确切的几何关系。我们用图三来说明这一总所周知的关系。正如图三所示,深度图捕捉每个像素上物体与相机的物理距离。而表面法线图描述了每个像素的法线向量,近似其在三维场景中的切平面。这很明显,在一个深度图的光滑区域,每个像素的法线方向不会改变太多。但是在不连续区域,每个像素的法线向量会变得很不同。因此,深度受到近似方向的表面法线决定的局部表面切平面的约束。与此同时,表面法线图与深度图的不一致性少于RGB-D图像对。我们已经使用图像1来展示使用彩色图引导和使用法线图引导的细化的深度图的视觉上的不同,其中放大因子为4。因此我们尝试去使用深度图和法线图的几何关系来提升恢复的深度图的准确性。表面法线图是由与低分辨率的深度图对应的高分辨率的彩色图生成的。正如图三所示,我们使用张英达提供的方法来从一张彩色图来估计法线图。在表面法线图中,颜色的改变代表物体法线方向的变化。
2.1.1 坐标转换系统
我们定义(ui,vi) 为像素i在2D图像中的位置。它在3D空间中对应的位置为(xi,yi,zi),其中zi是深度。基于针孔相机模型,我们得到如下公式:
xi=(ui-cx)*zi/fx;
yi=(vi-cy)*zi/fy;
其中,fx和fy代表着沿着x和y方向的焦距,cx和cy是主点的坐标。论文存疑:什么是主点?
2.1.2 法线到深度估计算子(NTD)
对于任意一个像素i,给出它估计的表面法线(nix,niy,niz)和一个小的领域,目标是细化它的深度。首先,根据给出的3D点(xi,yi,zi)和它的表面法线(nix,niy,niz),我们可以唯一确定切平面Pi,其满足的公式如下:
nix(x-xi) + niy(y-yi) + niz(z-zi) = 0 (3)
我们仍然可以假设像素i小领域内的像素也位于这个切平面Pi上,并且这个领域Mi可以定义如下:
Mi = (xi,yi,zi)|nTj*ni > α,|ui-uj|<β,|vi-vj|<β (4)
其中,β是控制领域大小的参量,α是一个阈值,来判断其他点是否与Pi点在一个近似共面上。对于任何一个属于Mi平面的像素j,如果我们假设其深度zj是准确的,我们可以计算像素i的深度。它可以如下表示:
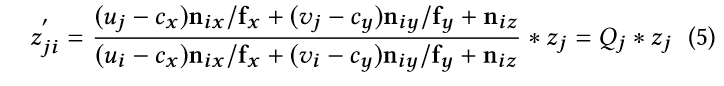
像素i的深度可以定义为:
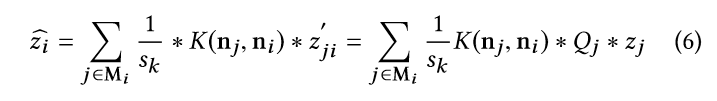
其中,zi为像素i的深度,sk是正则化因子,其中
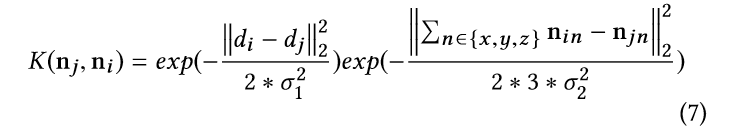
其中,di和dj是像素i和j的二维位置,它们的二范数的平方测量它们之间的几何距离,后面那项测量两者共面程度。参数δ1和δ2控制权重的敏感性。我们使用其他两个参数分别表示低分辨率的深度图和细化后的深度图,它们的关系表示如下:
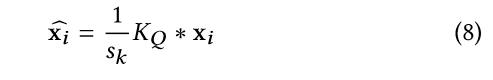
KQ是估计矩阵,它的第i列就是KQJ的向量形式。
2.2 图像拉普拉斯正则器
在深度恢复中,一个重要的信息先验就是在深度图中存在分段光滑特性,其中包含在光滑区域间的锋利边界。有研究显示,图像信号的平滑度先验可以有效恢复分段光滑信号。为了探索分段光滑特性,我们运用了一个图像信号光滑先验来代表深度图固有的分段光滑特性。
我们假设第i个小片xi上的像素可以被定义为加权无向图G(V,E,W)上的函数f。V是一系列顶点,E是边集,其中每条边都包含V中的两个顶点,W是一个对称加权矩阵,W(i,j) = W(j,i)。W(i,j)是顶点i和顶点j带有权重的边连接,它测量了这两个点的相似程度。我们进一步定义了对角矩阵D,其中的第i个对角元素是W第i行元素的和:
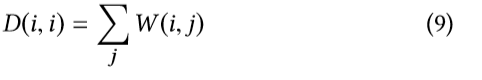
图像拉普拉斯矩阵定义如下:

它可以被归一化如下:

两点Vi和Vj两点的权重可以计算如下:
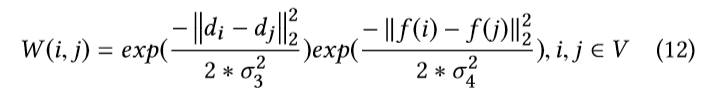
其中,di和dj代表像素i和像素j在二维图像中的位置。f(i)和f(j)代表顶点i和j的深度。根据上述定义,第一项测量顶点Vi和Vj的几何距离,第二项测量其在深度图中的光度距离。参数δ3和δ4控制几何距离和光度距离权重的敏感性。然后这个局部图像拉普拉斯正则器(GLR)对于xi被设计成如下最小化问题:
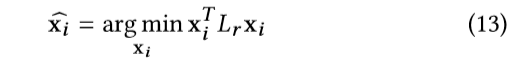
它也可以被重新写成下列形式:
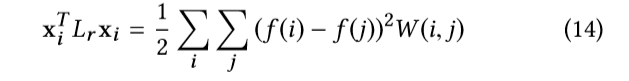
很明显的是如果恢复的切片在在两个相邻点具有相似值,或者融合项W(i,j)很小,则等式左边会很小。因此,通过最小化等式的左边,切片xi在局部结构会更光滑。
2.3 用正则器进行重建
为了得到一个高分辨率的切片,我们定义了一个模型,这个模型结合了法线到深度估计算子(NTD)和图像拉普拉斯正则器(GLR),这个模型可以被写成如下所示:
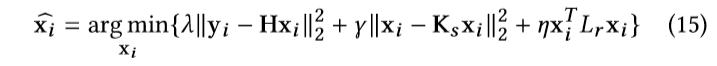
其中,xi是图像切片的向量形式,H是退化矩阵(降秩矩阵?),yi是观测到的像素的向量,ks是章节2.1中的归一化的估计算子。Lr是归一化的图像拉普拉斯矩阵,其他的是平衡参量。
上述最小化问题可以被下面近似形式问题有效地解决:
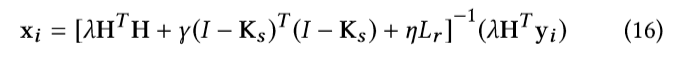
在实际操作中,我们不直接优化上述目标函数,我们将其重构为如下所示:
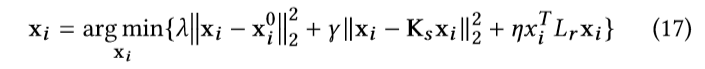
其中,xi0是通过经典地双三次插值方法的初始化插值结果。然后,我们优化目标函数(17)而不是(16),这样的话,估计结果xi(k)的第k次迭代可以被用作xi(0)的k+1次迭代。目标函数(17)当然也可以用很多其他的方法来解决,比如共轭梯度法不用矩阵的逆。算法1总结了提出的深度图恢复方法的完整程序。

3.实验结果
3.1 实验设置
因为缺少表面法线图的标签,现存的估计表面法线的方法是用数据集来训练一个卷积神经网络。这个数据集可以由合成表面法线图和对应的彩色图组成,或者相同的3D场景的低分辨率深度图。参考文献【13】已经做了对比实验,并且生动地展示了从彩色图获得的法线图比从低分辨率获得的深度图要准确。因此,我们使用参考文献【13】所提供的方法来获得表面法线数据。我们选择 Middlebury Stereo 2014 Dataset【1】来作为测试集,其中提供了一个特别重要的信息,相机内部参数校准后的深度图。根据章节2.1,我们知道相机内部参数校准是坐标转换系统的关键。低分辨率的深度图是从对应的高分辨率的深度图下采样得到的。然后通过预训练好的模型,我们得到了对应的表面法线图。我们经验性地将整个深度图分成10x10的切片,并且结果表现良好。对于更大的上采样因子,例如8,我们应用我们的超分辨方法三次来获得最后的结果。


3.2 对比实验
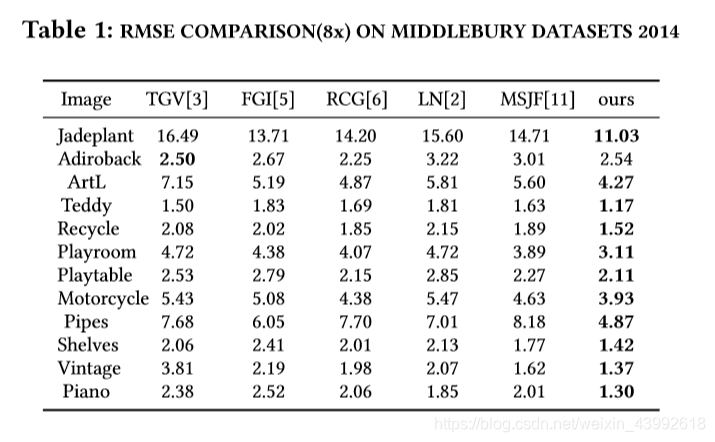
为了评估我们方法的表现,我们和其他五种主流的方法进行了比较:TGV[3],FGI[5],RCG[6],LN[2],MSJF[11]。在这些方法中,RCG[6],LN[2],MSJF[11]c采用了标注好的彩色图像的信息作为引导,而TGV[3],FGI[5]是深度恢复目前最好的框架。正如章节2.3所示,我们的方法联合使用了NTD正则化和GLR正则化,我们将其称为联合框架。为了研究这两种正则化对最终结果的贡献,我们也做了控制变量的实验,只使用其中一种正则化。这些对比实验生动地展示了表面法线图提供的几何关系对深度恢复的有效性。为了公平地进行比较,我们采用了相同的实验设置,例如测试集、切片尺寸、重叠的大小(?),双三次插值都采用了初始方法相同的设置。均方根误差(RMSE),绝对平均差(MAD)被采用作为定量测量的标准,不计算高分辨率深度图中的空洞。
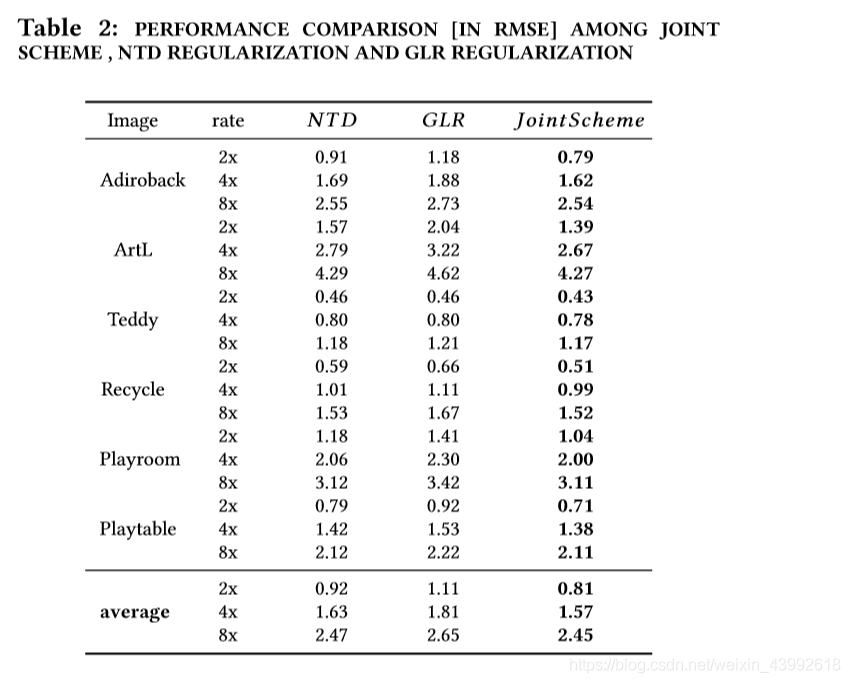
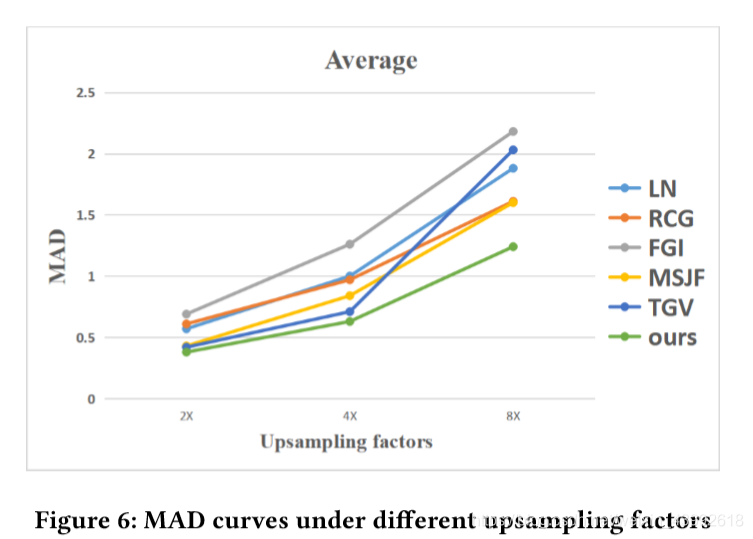
大量的测试集的比较在table1中展示,其中,上采样因子是8,评价标准是RMSE。table2展示了两种正则化不同的贡献。不同方法在Recycle数据集和ArtL数据集的视觉比较在图四和图五中展示,放大因子分别为4和8。对于不同的上采样因子,我们比较了不同方法恢复结果的平均值,标准是MAD,正如图六所示。
3.3 实验结果分析
正如表一与图六所示,我们的方法比其他方法表现的更好,在RMSE和MAD作为标准下。在图四和图五中,我们可以看到我们的方法有效地减轻了彩图引导方法的物体的缺陷。在一方面,表面法线可以在局部地方提供更多的空间结构,而且在图四中很清晰地显示了表面法线和深度图的几何关系帮助恢复的结果更加靠近真实结果的结构。在另一方面,与RGB-D图像对相比更少的纹路不一致减少了重建过程中的错误,这在图五中很清晰地显示了。同样的,正如表二所示,我们可以发现,NTD正则化比GRL正则化更加可靠,而且这两个正则化是互补的。通过将它们放在一起,我们取得了比只使用一种方法更好的结果。
由于表面法线图是一个估计的结果,这直接影响了重建的结果。另一个问题是在边界估计正确的法线很困难,这也影响了边界区域的重建结果。正如图三图四所示,作为一个比较,那些彩图引导的方法例如RCG[6]和LN[2]可以得到更锋利的边界因为我们估计的表面法线是模糊的当深度在边界有较大的转变。然而,我们的方法可以更好地保存边界框架,而且不用像彩图引导法需要大量的人工。
4.结论
在这篇论文中,我们利用了3D场景中的表面法线和物体到摄像机距离的几何关系设计了一个原创的深度恢复估计算子。这个估计算子提供了更多的在相邻像素中的空间几何关系,这帮助最后重建的结果在空间结构上更加地靠近真值。而且,为了保护深度图固有的分段光滑特性,我们也应用了一个图像拉普拉斯先验在深度图恢复中作为一个局部约束。大量的实验结果证明了我们方法的有效性。
- Person Re-identification with Deep Similarity-Guided Graph Neural Network 论文笔记
- 子空间学习论文笔记02:Laplacian Eigenmaps for Dimensionality Reduction and Data Representation
- 论文笔记:Person Re-identification with Deep Similarity-Guided Graph Neural Network
- Monocular Relative Depth Perception with Web Stereo Data Supervision 论文笔记
- 《Data Recovery on Encrypted Databases With k-Nearest Neighbor Query Leakage》论文翻译
- 论文笔记之---Learning Deep Feature Representations with Domain Guided Dropout for Person Re-identificatio
- Fast Failure Detection and Recovery in SDN with Stateful Data Plane
- 【论文翻译】Real-Time User-Guided Image Colorization with Learned Deep Priors
- produce a gradient file using surface elevation data, and plot it using grdimage with topographic "shade"
- 论文笔记之:Deep Generative Image Models using a Laplacian Pyramid of Adversarial Networks
- 论文笔记-深度估计(5)Unsupervised Monocular Depth Estimation with Left-Right Consistency
- TAO: Facebook's Distributed Data Store for the Social Graph论文阅读笔记
- 论文阅读笔记—Reasoning on Knowledge Graphs with Debate Dynamics(AAAI,2020)
- Knowledge-aware Graph Neural Networks with Label Smoothness Regularization for Recommender Systems
- 5: Which Domains Were Submitted Most Often?(Guided Project: Transforming data with Python )
- 论文笔记——Creating Speech and Language DataWith Amazon’s Mechanical Turk
- 【论文阅读】Deep Reasoning with Knowledge Graph for Social Relationship Understanding
- Laplacian surface editing
- [论文阅读笔记]DyTa: dynamic symbolic execution guided with static verification results
