逻辑回归算法梳理
逻辑回归算法梳理
1. 逻辑回归原理
逻辑回归是一个机器学习分类算法,它将数据拟合到一个logit函数(或者叫做logistic函数)中,从而能够对事件发生的概率进行预测,根据这个概率与设定的阈值作比较,从而实现分类功能。
1.1 由来
回归任务是结果为连续型变量的任务,而分类是离散型结果,那竟然是分类,为什么名字叫回归呢?其实逻辑回归就是用回归的办法来做分类,逻辑回归模型是在线性模型基础上套了一个函数把连续值转为离散值。
考虑最简单的二分类,结果是正例或者负例的任务。例如预测一个人"有"或者"没有"得恶性肿瘤,可以先通过线性回归任务来预测人体内肿瘤的大小,获取回归线,然后取一个平均值作为阈值f,肿瘤大小超过f为恶心肿瘤,无肿瘤或大小小于f的为非恶性。这样通过线性回归加设定阈值的办法,就可以完成一个简单的二分类任务。
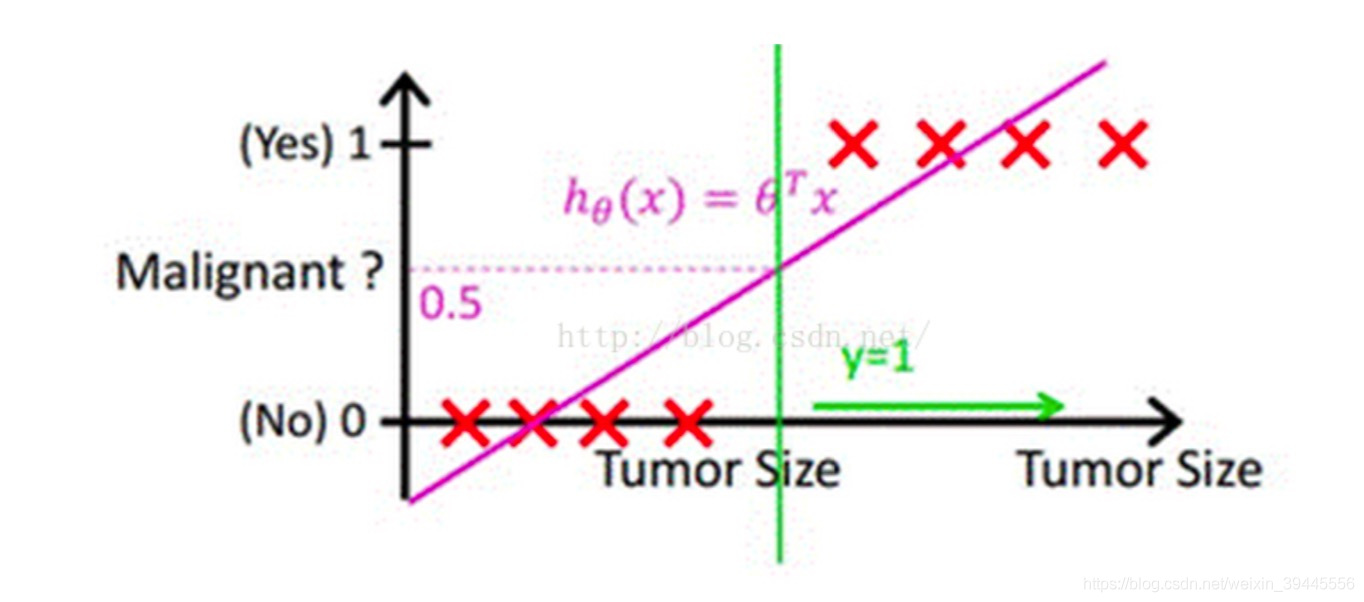
上图中,x轴为肿瘤大小,粉色的线为回归出的函数hΘ(x)h_{\Theta }(x)hΘ(x),绿色的线为阈值。
1.2 Sigmoid函数以及设定阈值
但是,当出现一些离群值时,回归函数会被带偏,并且很难设定阈值(是舍去离群值还是直接取平均),会出现下图情况:
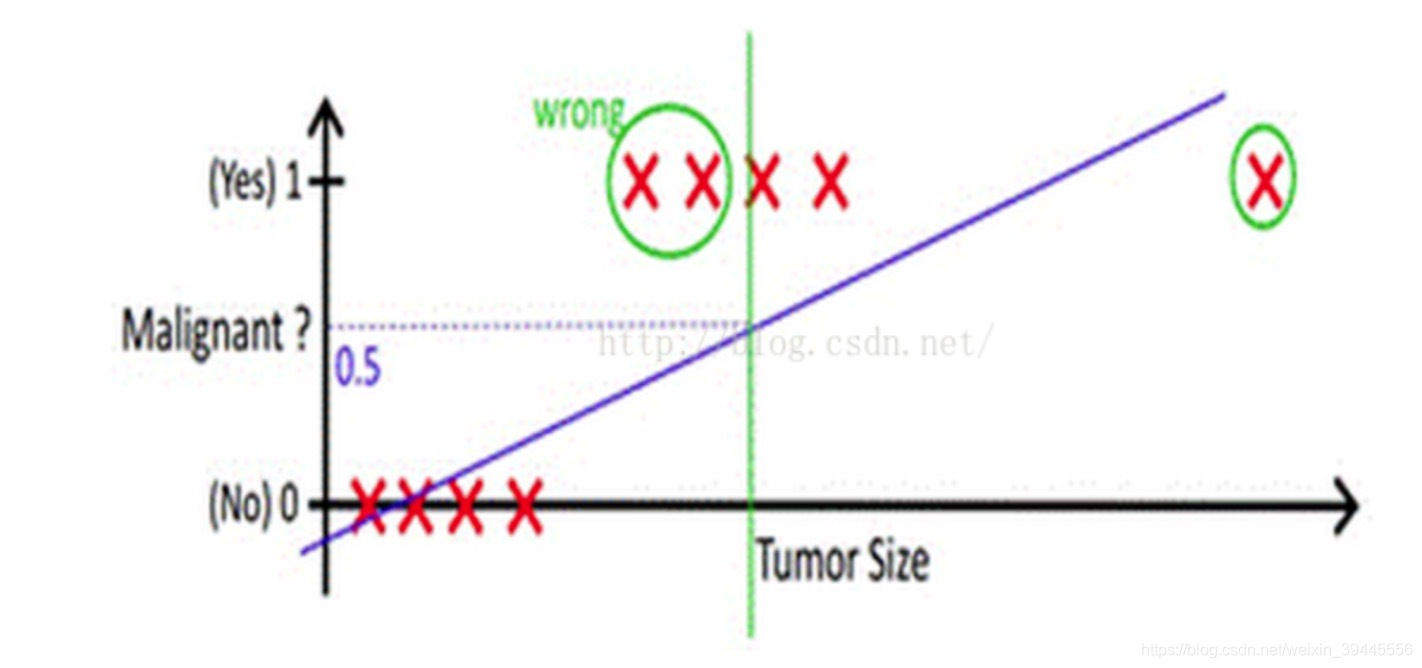
于是,我们要做两件事:
- 使回归函数不受离群值影响;
- 选定一个合适的阈值。
1.2.1 Sigmoid函数
原来的判别函数我们用线性的y = wTxw^{T}xwTx,逻辑回归的函数目前就用sigmod函数,函数如下:
g(z)=11+e−zg(z)=\frac{1}{1+e^{-z}}g(z)=1+e−z1
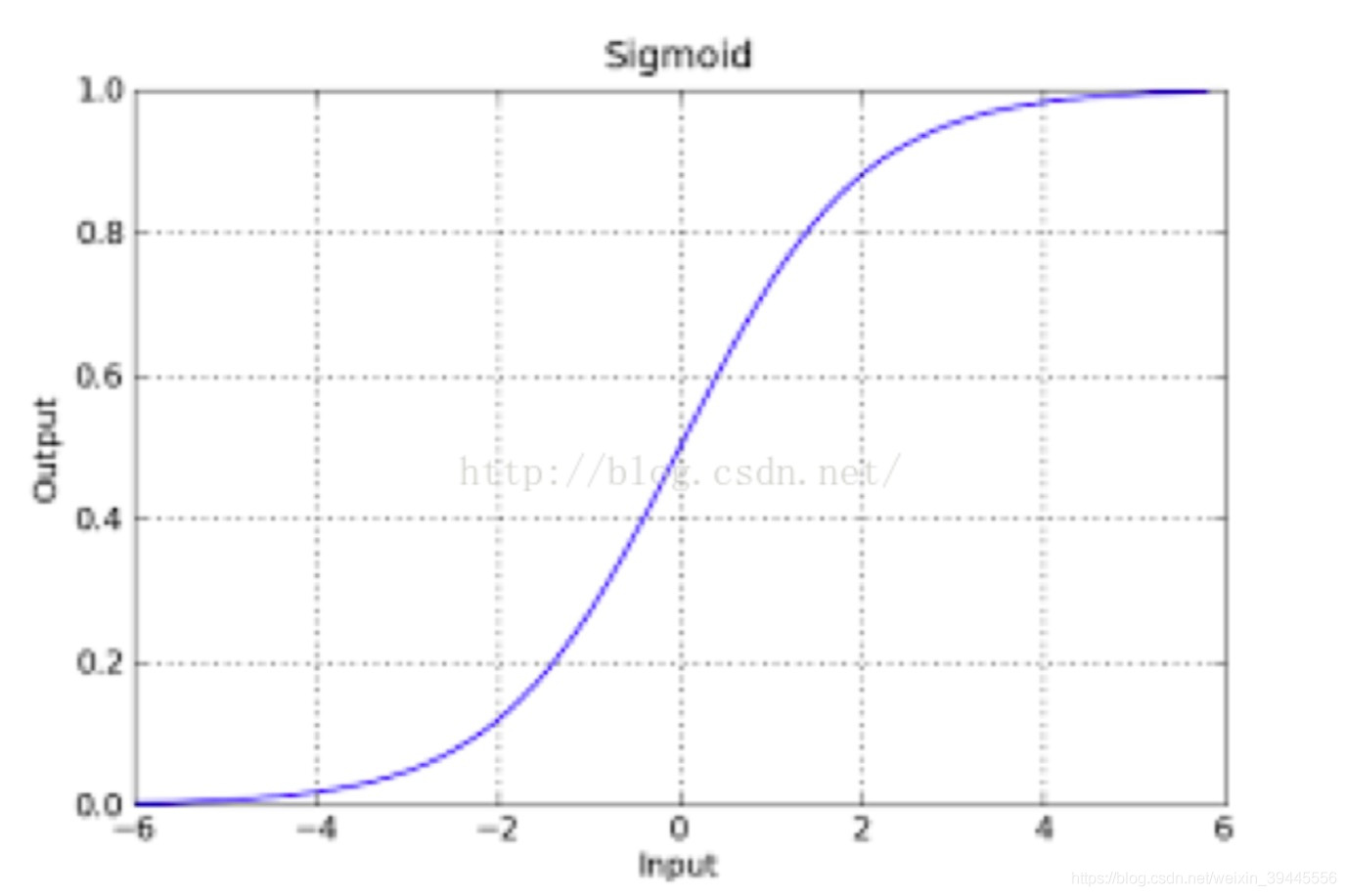
该函数具有很强的鲁棒性,并且将函数的输入范围(∞,-∞)映射到了输出的(0,1)之间且具有概率意义。具有概率意义是怎么理解呢:将一个样本输入到我们学习到的函数中,输出0.7,意思就是这个样本有70%的概率是正例,1-70%就是30%的概率为负例。
回到之前的问题:利用线性回归的办法来拟合然后设置阈值的办法容易受到离群值的影响,sigmod函数可以有效的帮助我们解决这一个问题,所以我们只要在拟合的时候把y = θ0x0+θ1x1+...+θnxnθ_{0}x_{0} + θ_{1}x_{1} + ... +θ_{n}x_{n}θ0x0+θ1x1+...+θnxn即y = θTXθ^{T}XθTX换成g(z)=11+e−zg(z) = \frac{1}{1+e^{-z}}g(z)=1+e−z1即可,其中
z=θTXz=θ^{T}Xz=θTX,也就是g(z)=11+e−θTxg(z) = \frac{1}{1 + e^{-θ^{T}x}}g(z)=1+e−θTx1,然后刚才说到的概率就是:
P(y=1|θ,x) = g(z)
P(y=0|θ,x) = 1 – g(z)
1.2.1 设定合适的阈值
Sigmoid函数预测结果为一个0到1之间的小数,选定阈值的第一反应大多都是选0.5(通常为0.5),但这要根据实际情况来确定。
例如前面的例子,如果一个患者得恶性肿瘤的概率为0.49,模型依旧认为他没有患恶性肿瘤,结果就造成了严重的医疗事故。此类情况我们应该将阈值设置的小一些。
1.3 决策边界
我们现在再来看看,为什么逻辑回归能够解决分类问题。这里引入一个概念,叫做决策边界,可以理解为是用以对不同类别的数据分割的边界,边界的两旁应该是不同类别的数据。
举几个例子:
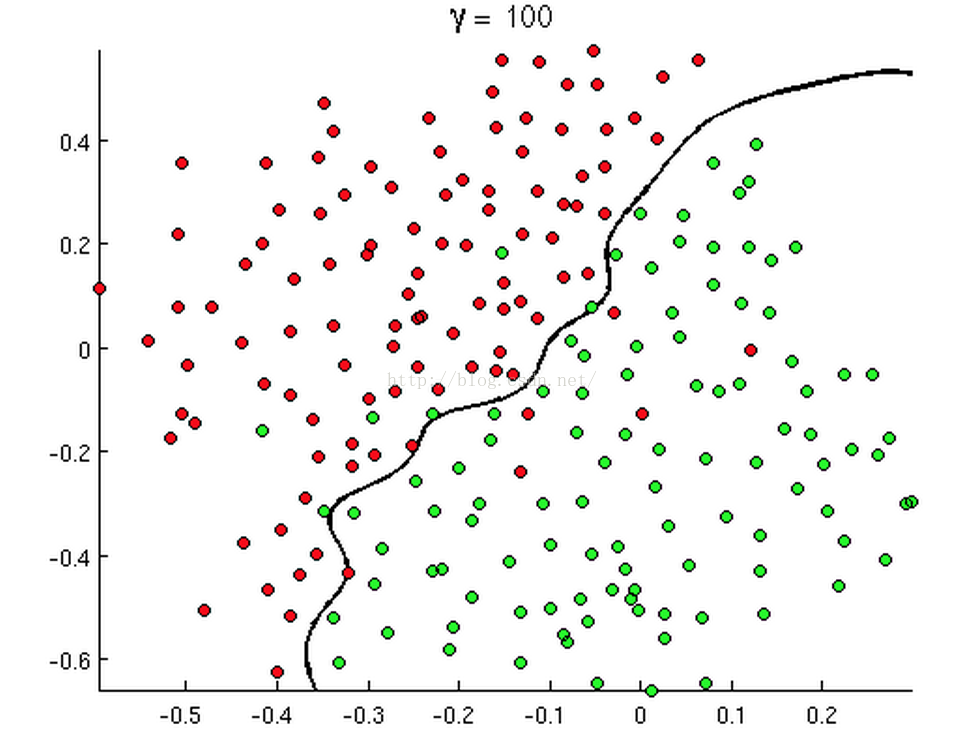
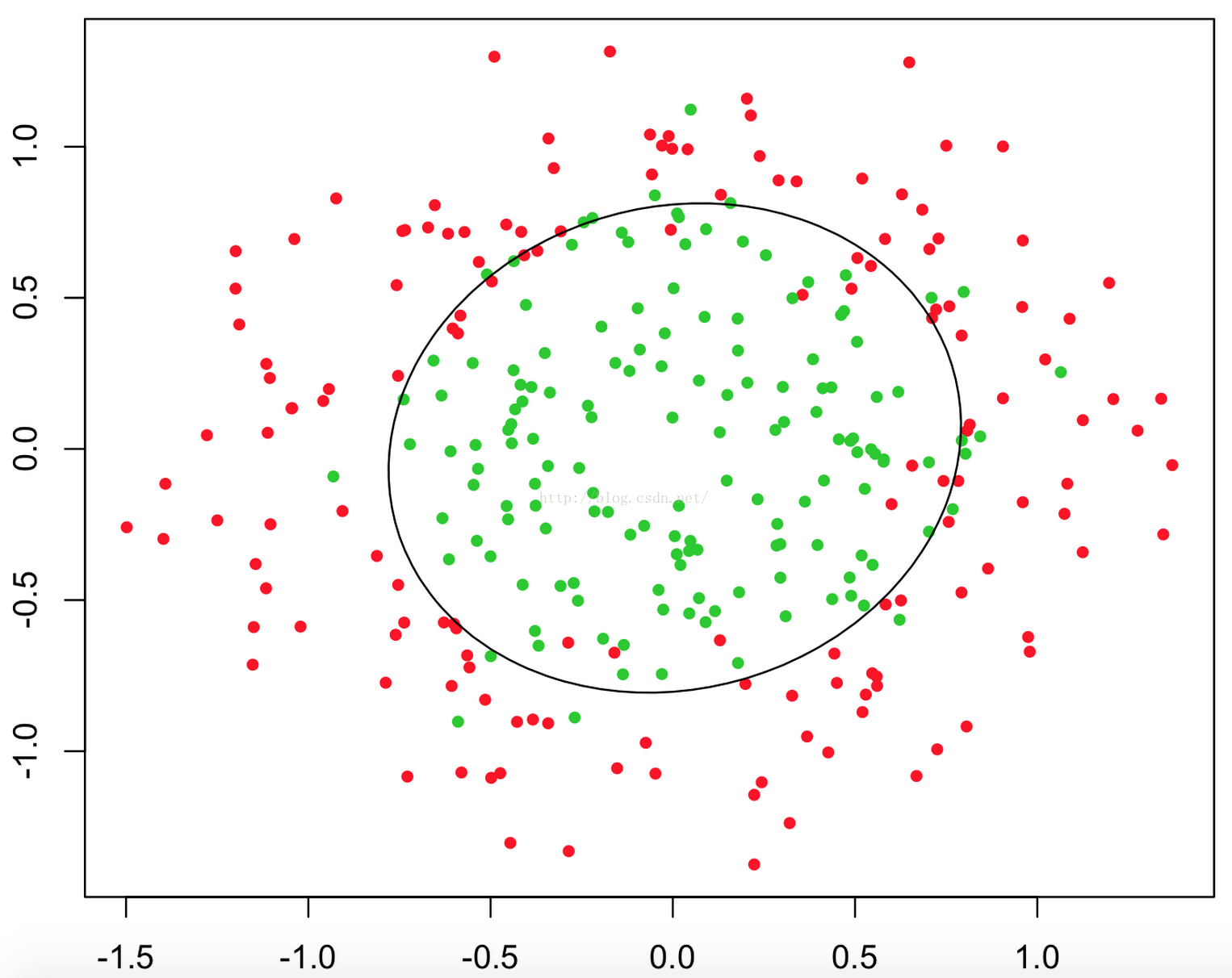
那么逻辑回归是如何根据样本点获得这些判定边界的呢?
回到Sigmoid函数,当我们的阈值选择为0.5时,Sigmod函数如下:

我们发现:当g(z)≥0.5时, z≥0;
对于hθ(x)=g(θTX)≥0.5h_θ(x)=g(θ^TX)≥0.5hθ(x)=g(θTX)≥0.5, 则θTX≥0θ^TX≥0θTX≥0, 此时意味着预估y=1;反之,当预测y = 0时,θTX<0θ^TX<0θTX<0。
所以我们认为θTX=0θ^TX =0θTX=0是一个决策边界,当它大于0或小于0时,逻辑回归模型分别预测不同的分类结果。
所以理论上说,只要我们的hθ(x)h_θ(x)hθ(x)设计足够合理,准确的说是g(θTx)g(θ^Tx)g(θTx)中θTxθ^TxθTx足够复杂,我们能在不同的情形下,拟合出不同的(线性或者非线性)决策边界,从而把不同的样本点分隔开来(注意:决策边界由参数θ决定,而不是由数据集x决定)。
2. 逻辑回归损失函数推导及最优化
我们通过对决策边界的说明,知道会有合适的参数θ使得θTx=0θ^Tx=0θTx=0成为很好的分类决策边界,那么问题就来了,我们如何判定我们的参数θ是否合适,有多合适呢?更进一步,我们有没有办法去求得这样的合适参数θ呢?这就要提及损失函数以及梯度下降法了。
2.1 损失函数
所谓的(损失函数)代价函数Cost Function,其实是一种衡量我们在这组参数下预估的结果和实际结果差距的函数,比如说线性回归的代价函数定义为:
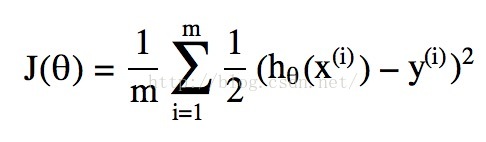
当然我们可以和线性回归类比得到一个代价函数,实际就是上述公式中hθ(x)h_θ(x)hθ(x)取为逻辑回归中的g(θTx)g(θ^Tx)g(θTx),但是这会引发代价函数为“非凸”函数的问题,简单一点说就是这个函数有很多个局部最低点,如下图所示:
那么如何解决呢?先直接给出逻辑回归的损失函数的简化版:
cost(hθx,y)={−log(hθ(x)),if y=1−log(1−hθ(x)),if y=0cost(h_θx,y)= \left\{
\begin{aligned}
& -log(h_θ(x)),if\ y=1\\
& -log(1-h_θ(x)) ,if\ y=0\\
\end{aligned}
\right.
cost(hθx,y)={−log(hθ(x)),if y=1−log(1−hθ(x)),if y=0
可以看到取了对数,可以把y=1以及y=0的图画出来:
如果我们的类别y = 1, 而判定的hθ(x)=1h_θ(x)=1hθ(x)=1,则Cost = 0,此时预测的值和真实的值完全相等,代价本该为0;而如果判断hθ(x)→0h_θ(x)→0hθ(x)→0,代价->∞,这很好地惩罚了最后的结果。同理,对于y=0:
推导过程:
已经知道hθ(x)=g(θTX)=g(z)h_θ(x)=g(θ^TX)=g(z)hθ(x)=g(θTX)=g(z)
所以,{P(y=1∣θ,x)=g(z)=hθ(x)P(y=0∣θ,x)=1–g(z)=1−hθ(x) \left\{
\begin{aligned}
& P(y=1|θ,x) = g(z)= h_θ(x)\\
& P(y=0|θ,x) = 1 – g(z)=1- h_θ(x)
\end{aligned}
\right.
{P(y=1∣θ,x)=g(z)=hθ(x)P(y=0∣θ,x)=1–g(z)=1−hθ(x)
联合起来即:P(y∣x;θ)=(hθ(x))y(1−hθ(x))1−yP(y|x;θ)=(h_θ(x))^y(1-h_θ(x))^{1-y}P(y∣x;θ)=(hθ(x))y(1−hθ(x))1−y
取似然函数:
L(θ)=∏i=1mP(y(i)∣x(i);θ)=∏i=1m(hθ(x(i)))y(i)(1−hθ(x(i)))1−y(i)
\begin{aligned}
L(θ) &= \prod_{i=1}^{m} P(y^{(i)}|x^{(i)};θ)\\
& =\prod_{i=1}^{m} (h_θ(x^{(i)}))^{y^{(i)}}(1-h_θ(x^{(i)}))^{1-y^{(i)}}
\end{aligned}
L(θ)=i=1∏mP(y(i)∣x(i);θ)=i=1∏m(hθ(x(i)))y(i)(1−hθ(x(i)))1−y(i)
对数似然函数:
l(θ)=logL(θ)=∑i=1m(y(i)log(hθ(x(i)))+((1−y(i))log(1−hθ(x(i))))
\begin{aligned}
l(θ) &=log L(θ)\\
& =\sum_{i=1}^{m} ({y^{(i)}}log(h_θ(x^{(i)}))+((1-y^{(i)})log(1-h_θ(x^{(i)})))
\end{aligned}
l(θ)=logL(θ)=i=1∑m(y(i)log(hθ(x(i)))+((1−y(i))log(1−hθ(x(i))))
使损失函数J(θ)=−1ml(θ)J(θ)=-\frac{1}{m}l(θ)J(θ)=−m1l(θ),最大似然估计就是求使 l(θ)l(θ)l(θ) 取最大值时的 θ ,其实这里可以使用梯度上升法求解,求得的 θ 就是要求的最佳参数。因为乘了一个负的系数 −1m-\frac{1}{m}−m1 ,所以取 J(θ) 最小值时的θ为要求的最佳参数。θ知道了,就相当于决策边界知道了。
2.2 梯度下降法
利用梯度下降法求使J(θ)取最小值时的θ:
θj:=θj−αJ′(θ)θ_j:=θ_j-\alpha J ^\prime(θ)θj:=θj−αJ′(θ)
这里我们把log变成ln,即
J(θ)=−1m∑i=1m(y(i)ln(hθ(x(i)))+((1−y(i))ln(1−hθ(x(i))))J(θ)=-\frac{1}{m}\sum_{i=1}^{m} ({y^{(i)}}ln(h_θ(x^{(i)}))+((1-y^{(i)})ln(1-h_θ(x^{(i)})))J(θ)=−m1∑i=1m(y(i)ln(hθ(x(i)))+((1−y(i))ln(1−hθ(x(i))))
并且:hθ(x)=g(θTX)=g(z)h_θ(x)=g(θ^TX)=g(z)hθ(x)=g(θTX)=g(z),g′(z)=g(z)(1−g(z))g^\prime(z)=g(z)(1-g(z))g′(z)=g(z)(1−g(z))
δδθjJ(θ)=−1m∑i=1m(y(i)1hθ(x(i))δδθjhθ(x(i))−(1−y(i))11−hθ(x(i))δδθjhθ(x(i)))=−1m∑i=1m(y(i)1g(θTx(i))−(1−y(i))11−g(θTx(i)))δδθjg(θTx(i))=−1m∑i=1m(y(i)1g(θTx(i))−(1−y(i))11−g(θTx(i)))g(θTx(i))(1−g(θTx(i)))δδθjθTx(i)=−1m∑i=1m(y(i)(1−g(θTx(i)))−(1−y(i))g(θTx(i)))xj(i)=−1m∑i=1m(y(i)−g(θTx(i)))xj(i)=1m∑i=1m(hθ(x(i))−y(i))xj(i)
\begin{aligned}
\frac{\delta}{\delta_{\theta_j}}J(\theta)
=&-\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}\frac{1}{h_\theta(x^{(i)})}\frac{\delta}{\delta_{\theta_j}}h_\theta(x^{(i)})-(1-y^{(i)})\frac{1}{1-h_\theta(x^{(i)})}\frac{\delta}{\delta_{\theta_j}}h_\theta(x^{(i)}))\\
=&-\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}\frac{1}{g(\theta^Tx^{(i)})}-(1-y^{(i)})\frac{1}{1-g(\theta^Tx^{(i)})})\frac{\delta}{\delta_{\theta_j}}g(\theta^Tx^{(i)})\\
=&-\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}\frac{1}{g(\theta^Tx^{(i)})}-(1-y^{(i)})\frac{1}{1-g(\theta^Tx^{(i)})})g(\theta^Tx^{(i)})(1-g(\theta^Tx^{(i)}))\frac{\delta}{\delta_{\theta_j}}\theta^Tx^{(i)}\\
=&-\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}(1-g(\theta^Tx^{(i)}))-(1-y^{(i)})g(\theta^Tx^{(i)}))x_j^{(i)}\\
=&-\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}-g(\theta^Tx^{(i)}))x_j^{(i)}\\
=&\frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}
\end{aligned}
δθjδJ(θ)======−m1i=1∑m(y(i)hθ(x(i))1δθjδhθ(x(i))−(1−y(i))1−hθ(x(i))1δθjδhθ(x(i)))−m1i=1∑m(y(i)g(θTx(i))1−(1−y(i))1−g(θTx(i))1)δθjδg(θTx(i))−m1i=1∑m(y(i)g(θTx(i))1−(1−y(i))1−g(θTx(i))1)g(θTx(i))(1−g(θTx(i)))δθjδθTx(i)−m1i=1∑m(y(i)(1−g(θTx(i)))−(1−y(i))g(θTx(i)))xj(i)−m1i=1∑m(y(i)−g(θTx(i)))xj(i)m1i=1∑m(hθ(x(i))−y(i))xj(i)
于是,θj:=θj−α1m∑i=1m(hθ(x(i))−y(i))xj(i)θ_j:=θ_j-\alpha \frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}θj:=θj−αm1∑i=1m(hθ(x(i))−y(i))xj(i)
好,总结一下,一般回归问题的三个重要步骤:
- 寻找h函数(即预测函数);
- 构造J函数(损失函数);
- 想办法使得J函数最小并求得回归参数(θ);各种最优化方法,梯度下降、随机梯度下降、牛顿法等。
参考:https://skyelan.github.io/2019/03/31/PrimaryAlgorithm/PrimaryAlgorithm2/
3. 正则化
在线性回归算法梳理那一篇blog中说到,正则化的作用是选择经验风险与模型复杂度同时较小的模型来避免过拟合。常见的有L1正则化、L2正则化。
3.1 L1正则化
L1正则化就是在原始的代价函数后面加上一个L1正则化项,即所有权重θ的绝对值的和,乘以λn\frac{\lambda}{n}nλ。C0C_0C0为原始的损失函数(代价函数),λ\lambdaλ为惩罚项系数,n为训练集样本大小。
C=C0+λn∑θ∣θ∣C = C_0+\frac{\lambda}{n}\sum_θ{|θ|}C=C0+nλθ∑∣θ∣
求导:
∂C∂θ=∂C0∂θ+λnsgn(θ)\frac{\partial C}{\partial θ} = \frac{\partial C_0}{\partial θ} +\frac{\lambda}{n}sgn(θ)∂θ∂C=∂θ∂C0+nλsgn(θ)
θ的更新规则为:
θ−> θ′=θ−α∂C0∂θ−αλnsgn(θ)θ -> \ θ^\prime = θ-\alpha \frac{\partial C_0}{\partial θ} - \frac{\alpha \lambda}{n}sgn(θ)θ−> θ′=θ−α∂θ∂C0−nαλsgn(θ)
所以当θ>0时,更新后θ变小;当θ<0时,更新后θ变大。所以它的作用就是使θ往0靠,使权重尽可能为0,相当于减少了模型复杂度,防止过拟合。
3.2 L2正则化
C=C0+λ2n∑θθ2C = C_0 +\frac{\lambda}{2n}\sum_θ{θ^2}C=C0+2nλθ∑θ2
求导:
∂C∂θ=∂C0∂θ+λnθ
\begin{aligned}
\frac{\partial C}{\partial θ} =& \frac{\partial C_0}{\partial θ} +\frac{\lambda}{n}θ
\end{aligned}
∂θ∂C=∂θ∂C0+nλθ
更新规则:
θ−> θ′=θ−α∂C0∂θ−αλnθ=(1−αλn)θ−α∂C0∂θ
\begin{aligned}
θ -> \ θ^\prime =& θ-\alpha \frac{\partial C_0}{\partial θ} - \frac{\alpha \lambda}{n}θ \\
=& (1- \frac{\alpha \lambda}{n}) θ -\alpha \frac{\partial C_0}{\partial θ}
\end{aligned}
θ−> θ′==θ−α∂θ∂C0−nαλθ(1−nαλ)θ−α∂θ∂C0可以知道,由于步长α\alphaα、惩罚项系数λ\lambdaλ、样本集数n都是正的,所以(1−αλn)(1- \frac{\alpha \lambda}{n})(1−nαλ)小于1,效果是减少权重θ(权重衰减),更小的权值,表示复杂度更低。
4. 模型评估指标
4.1 准确率、召回率、F1值
一般来说,正确率(Precision)就是检索出来的条目有多少是正确的,召回率(Recall)就是所有正确的条目有多少被检索出来了。
F1值是综合上面二个指标的评估指标,因为有时候Precision和Recall会有矛盾,就是Precison越高(越低),Recall越低(越高),因此考虑综合反映整体的指标,公式如下:

这几个指标的取值都在0-1之间,数值越接近于1,效果越好。
举个例:
某池塘有1400条鲤鱼,300只虾,300只鳖。现在以捕鲤鱼为目的。
撒一大网,逮着了700条鲤鱼,200只虾,100只鳖。那么,这些指标
分别如下:
Precision= 700 / (700 + 200 + 100) = 70%
Recall= 700 / 1400 = 50%
F1值= 70% * 50% * 2 / (70% + 50%) = 58.3%
这里还有个P-R曲线,这里可以看出P与R的矛盾,如下图:

精确率越高,召回率越高,我们的模型和算法就越高效,也就是画出来的PR曲线越靠近右上越好。
4.2 ROC、AUC
先提及一下概念:

TP:True Positive,“真阳性”
FP:False Positive,“假阳性”
FN:False Negative,“假阴性”
TN:True Negative,“真阴性”
下图为ROC曲线:

横坐标为FPR=FPFP+TNFPR=\frac{FP}{FP+TN}FPR=FP+TNFP,预测的正类中,实际负类占所有负类的比例;
纵坐标为TPR=TPTP+FNTPR=\frac{TP}{TP+FN}TPR=TP+FNTP,预测的正类中,实际正类占所有正类的比例。
一连串这样的点构成了一条曲线,该曲线就是ROC曲线。而ROC曲线下的面积就是AUC(Area under the curve of ROC)。这就是AUC指标的由来。
这时就会有疑问了:对于一个特定的分类器和测试数据集,显然只能得到一个分类结果,即一组FPR和TPR结果,而要得到一个曲线,我们实际上需要一系列FPR和TPR的值才能得到这样的曲线,这又是如何得到的呢?
可以通过分类器的一个重要功能“概率输出”,即表示分类器认为某个样本具有多大的概率属于正样本(或负样本),来动态调整一个样本是否属于正负样本,例如逻辑回归的“正样本概率”P(y=1|θ,x)。
举个例子:
下图中共有20个测试样本,“Class”一栏表示每个测试样本真正的标签(p表示正样本,n表示负样本),“Score”表示每个测试样本属于正样本的概率。

接下来,我们从高到低,依次将“Score”值作为阈值,当测试样本属于正样本的概率大于或等于这个阈值时,我们认为它为正样本,否则为负样本。举例来说,对于图中的第4个样本,其“Score”值为0.6,那么样本1,2,3,4都被认为是正样本,因为它们的“Score”值都大于等于0.6,而其他样本则都认为是负样本。每次选取一个不同的阈值,我们就可以得到一组FPR和TPR,即ROC曲线上的一点。这样一来,我们一共得到了20组FPR和TPR的值,将它们画在ROC曲线的结果如下图:

AUC作为数值介于0.1和1之间,可以直观的评价分类器的好坏,值越大越好。
AUC值是一个概率值,当随机挑选一个正样本以及负样本,当前的分类算法根据计算得到的Score值将这个正样本排在负样本前面的概率就是AUC值,AUC值越大,当前分类算法越有可能将正样本排在负样本前面(正的在前,负的在后),从而能够更好地分类。
为什么要使用ROC曲线?
因为ROC曲线有个很好的特性:当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡(class imbalance)现象,即负样本比正样本多很多(或者相反),而且测试数据中的正负样本的分布也可能随着时间变化。将ROC与P-R曲线对比一下:
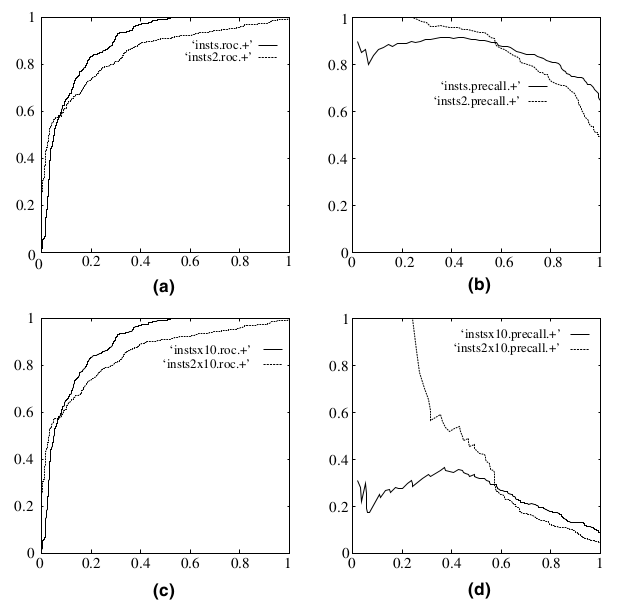
在上图中,(a)和(c)为ROC曲线,(b)和(d)为Precision-Recall曲线。(a)和(b)展示的是分类其在原始测试集(正负样本分布平衡)的结果,(c)和(d)是将测试集中负样本的数量增加到原来的10倍后,分类器的结果。可以明显的看出,ROC曲线基本保持原貌,而P-R曲线则变化较大。
转自:https://www.zybuluo.com/frank-shaw/note/152851
5. 逻辑回归的优缺点
优点:
1)经过了Sigmoid函数的映射,鲁棒性好,并且预测结果是界于0和1之间的概率;
2)可以适用于连续性和类别性自变量;
3)容易使用和解释;
4)训练速度快。
缺点:
1)由于sigmoid函数的特性,接近0/1的两侧概率变化较平缓,中间概率敏感,波动较大;导致很多区间特征变量的变化对目标概率的影响没有区分度,无法确定临界值;
2)容易欠拟合;
3)特征空间很大时效果不好。
6. sklearn参数
sklearn.linear_model.LogisticRegression(penalty=’l2’, dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver=’warn’, max_iter=100, multi_class=’warn’, verbose=0, warm_start=False, n_jobs=None)

