凸包算法的应用——数一数图形中共有多少三角形

一、问题引入

网络上经常会遇到判断图形个数的题目，如下例：

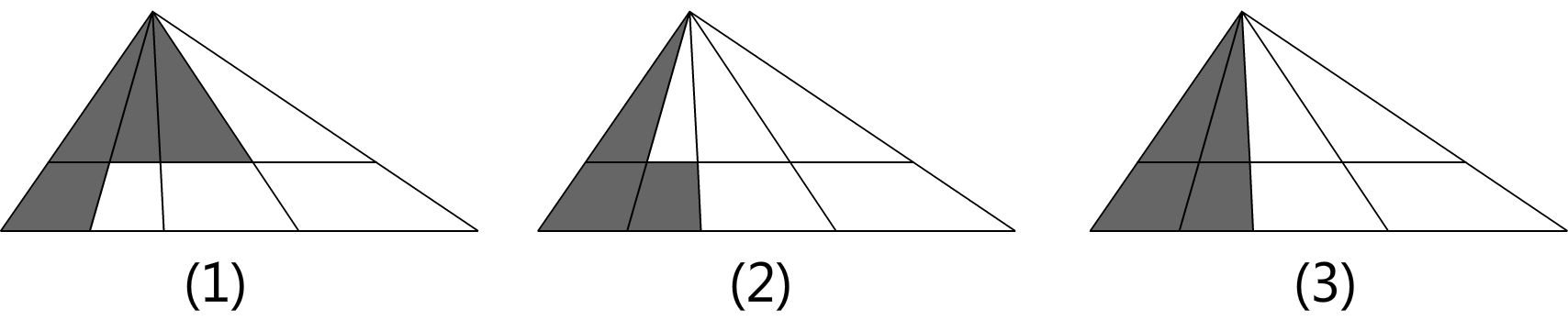
如果我们要把图中所有三角形一个一个选出来，在已知每个交点的前提下，该如何用代码判断我们选的图形是否是三角形呢。如下图，如何把图3筛选出来呢？

这里需要用到两步：

1.得到所选图形（阴影部分）所包含的所有小图形的顶点集合，求集合的凸包，根据凸包顶点个数判定凸包围成的图形是否是三角形，若顶点个数不为3则不是三角形，如图（1）。

.2.若凸包围成的图形是三角形，判断凸包的面积与所选图形（所有选中的小图形面积之和）是否相等，若相等则所选图形是三角形，若不相等则不是三角形，如上图（2）。

二、求点的凸包——Graham's Scan法介绍

（1）    什么是凸包

在二维欧几里得空间中，凸包可想象为一条刚好包着所有点的橡皮圈。

用不严谨的话来讲，给定二维平面上的点集，凸包就是将最外层的点连接起来构成的凸多边型，它能包含点集中所有的点。如下图红色部分：

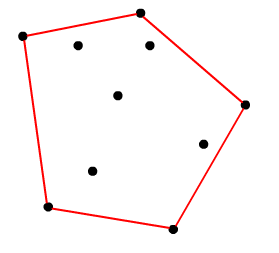
（2）    Graham's Scan法求凸包

这个算法是由数学大师葛立恒（Graham）发明的，算法思路如下：

1.找出所有点中y坐标最小的点，若y坐标最小的点有两个以上，则选择其中x坐标最小的点，将此点记为H；

2.设除H之外所有点的坐标集合为N{p1,p2,p3,p4,p5,p6,…}，分别计算向量< H,p1>，< H,p2>，< H,p3>极坐标的角度，对集合N按极坐标角度的大小排序，即以H为圆心，顺时针扫描各点，将扫描到的点依次加入集合中；如下图，排好序的坐标集合为N{a1，a2，a3，a4，a5，a6}，其中θ为向量< H,a1>极坐标的角度。

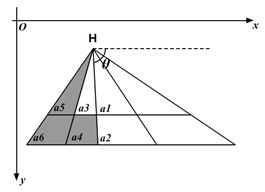
3.线段< H,a1>一定在凸包上，现在加入a2，假设a2也在凸包上，接下来加入a3，如果a3在向量<a1，a2>的左侧则判断a2不在凸包上，需将a2从凸包中移除，在此例中a3在向量<a1，a2>的右侧；然后加入a4，如果a4在向量<a2，a3>的左侧则判断a3不在凸包上，此例中a4在向量<a2，a3>的左侧，所以需将a3从凸包中移除，接下来需回溯判断a4在向量<a1，a2>的左侧还是右侧，决定是否要将a2移除…，即每加入一点时，必须考虑到前面的线段是否在凸包上。从基点开始，凸包上每条相临的线段的旋转方向应该一致，并与扫描方向相同。如果发现新加的点使得新线段与上线段的旋转方向发生变化，则可判定上一点必然不在凸包上。如下图：

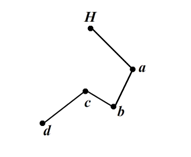
当加入d点时，发现<c,d>和<b,c>的旋转方向不一致(d在<b,c>左侧)，则说明c点不在凸包上。

可用叉积来判断一个点在一个向量的左侧还是右侧，如上图，若<b,c>与<c,d>的叉积为正则d在<b,c>的右侧，若为负则在<b,c>的右侧，若为0，在d在<b,c>直线上。

复杂度

这个算法可以直接在原数据上进行运算，因此空间复杂度为O⑴。但如果将凸包的结果存储到另一数组中，则可能在代码级别进行优化。由于在扫描凸包前要进行排序，因此时间复杂度至少为快速排序的O(nlgn)。后面的扫描过程复杂度为O(n)，因此整个算法的复杂度为O(nlgn)。

三、求解凸包的javascript代码

设数组points是存储所选图形的所有顶点的集合

var convexPoints=[];//用来存储凸包
var startPoint=getStartPoint(points);//得到y坐标最小的点
points.splice(points.indexOf(startPoint),1);
4 points.sort(compare);//按极坐标排序
convexPoints.push(startPoint);
convexPoints.push(points[0]);

for(i=1;i<points.length;i++){
var vector1={ x:convexPoints[convexPoints.length-1].x-convexPoints[convexPoints.length-2].x,
y:convexPoints[convexPoints.length-1].y-convexPoints[convexPoints.length-2].y};

var vector2={ x:points[i].x-convexPoints[convexPoints.length-1].x,
y:points[i].y-convexPoints[convexPoints.length-1].y};
//若两个向量叉积小于0，则需将上一个点移除
while(getCross(vector1,vector2)<0){
convexPoints.pop();
vector1={ x:convexPoints[convexPoints.length-1].x-convexPoints[convexPoints.length-2].x,
y:convexPoints[convexPoints.length-1].y-convexPoints[convexPoints.length-2].y};
vector2={ x:points[i].x-convexPoints[convexPoints.length-1].x,
y:points[i].y-convexPoints[convexPoints.length-1].y};
}
convexPoints.push(points[i]);
}

 求points集合中y坐标最小的点，y坐标相同的情况下，取x坐标最小的点

//选出y轴最小的点startPoint
function getStartPoint(points){
var startPoint=points[0];
for(var i=1;i<points.length;i++){
if(points[i].y<startPoint.y){
startPoint=points[i];
}else if(points[i].y==startPoint.y){
if(points[i].x<startPoint.x){
startPoint=points[i];
}
}
}
return startPoint
}

 按极坐标角度排序的compare函数

//各点按极坐标的角度排序
function compare(value1,value2){
var value1Angle=getPolarAngle(startPoint,value1);
var value2Angle=getPolarAngle(startPoint,value2);
if(value1Angle<value2Angle){
return -1;
}else if (value1Angle>value2Angle){
return 1;
}else{
return 0;
}
}

用此凸包判断所选图形是否是三角形时遇到的一个问题：

如下图所示，我们对阴影部分包含的点求凸包时，希望得到的是{A,B,C}三个点，这样我们通过判断凸包的大小即可知凸包的形状，而事实上我们通过以上算法求得的凸包可能会包含D，E，F，是否包含取决于对D，E，F坐标的采样精度，那么该如何从凸包中把这些点删掉呢？

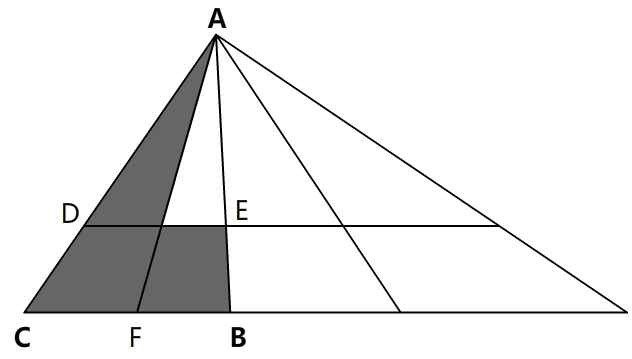
删除凸包中两个顶点组成的线段中间的点：如下图，当一条线段中间的点的采样坐标凹向图形内部的时候会被凸包算法排除掉（如D点），当采样坐标凸出来的时候就会被凸包算法计算在内（如E，F点），我们可以计算出<A,E>和<E,B>向量的夹角，当这个夹角小于某一范围时（取决于对采样误差的估算），我们就可认定E点在AB上，即可将E点从凸包中删除。按此方法依次检测凸包中所有的点，最后会得到我们选中的图形的各顶点。

代码如下：

1 //去掉一条线上中间的点,留下顶点
2 convexPoints.push(startPoint);//为了判定凸包最后一个点，需将起始点加在末尾形成一个环
3 deletePointIndexs=[];//存储要删除的点的索引
4 for(i=0;i<convexPoints.length-2;i++){
5     var vector1={x:convexPoints[i+1].x-convexPoints[i].x,y:convexPoints[i+1].y-convexPoints[i].y}
6     var vector2={x:convexPoints[i+2].x-convexPoints[i+1].x,y:convexPoints[i+2].y-convexPoints[i+1].y}
7     var angle=getAngle(vector1,vector2);
8     if(Math.abs(angle)<Math.PI/90){//误差范围设置为2度
9         deletePointIndexs.push(i+1);
10     };
11 }
12 if(deletePointIndexs.length>0){
13     for(i=deletePointIndexs.length-1;i>=0;i--){
14         convexPoints.splice(deletePointIndexs[i],1);
15     }
16 }
17 convexPoints.pop();//将起始点移除

当convexPoints的长度为3时，我们就可判定凸包所围成的图形是三角形。

四、通过面积的比较确定所选图形形状

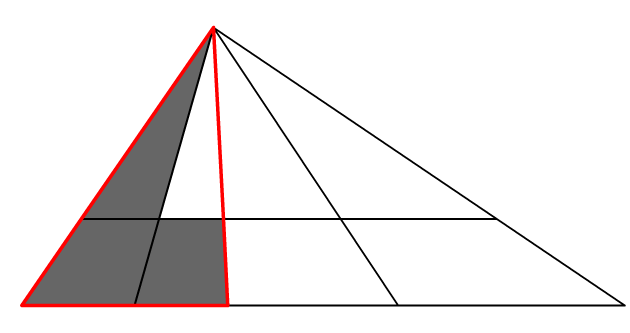
当我们所选形状是如下图形时，通过上面的凸包判断出来是三角形（红色部分），而实际不是。这种情况下我们可以通过比较所选图形的面积（阴影部分）与凸包所形成的图形的面积是否相等来最终确定图形形状。

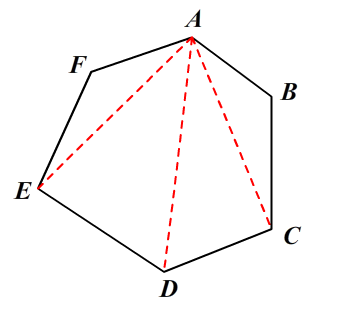
在已知一个多边形各顶点的情况下，可以通过将多边形分解为多个三角形进行计算，如下图。三角形面积可通过两条边向量的叉积求得；

计算多边形面积代码如下

//根据图形各顶点坐标求图形面积,思路：将多边形分解为多个三角形，利用叉积计算三角形面积
function getPolygonArea(pointData){
var area=0;
var startPoint=pointData[0];
for(var i=1;i<pointData.length-1;i++){
var vector1={x:pointData[i].x-startPoint.x,y:pointData[i].y-startPoint.y};
var vector2={x:pointData[i+1].x-pointData[i].x,y:pointData[i+1].y-pointData[i].y};
area+=Math.abs(getCross(vector1,vector2))/2;
}
return area;
}

 五、让程序自动选出所有三角形

我们可以遍历图形中小图形各种可能的排列组合，通过上述方式计算每一种组合拼成的是否是三角形，从而让程序帮我们判断图形共有多少三角形，并生成每一种三角形，具体实现不再赘述。

备注：用到的一些计算几何方面的工具

//得到向量极坐标的角度，p1和p2为向量的起点和终点
function getPolarAngle(p1,p2){
return Math.atan2(p2.y-p1.y,p2.x-p1.x);
}

//求两个向量的叉积
function getCross(vector1,vector2){
return vector1.x*vector2.y-vector2.x*vector1.y;
}

//求两向量的夹角
function getAngle(vector1,vector2){
return Math.acos(getDot(vector1,vector2)/(getLengthOfVector(vector1)*getLengthOfVector(vector2)));
}

//求向量的长度
function getLengthOfVector(vector){
return Math.sqrt(vector.x*vector.x+vector.y*vector.y);
}

//求两向量的点积
function getDot(vector1,vector2){
return vector1.x*vector2.x+vector1.y*vector2.y;
}