[SVM系列之二]线性分类
2018-03-05 13:29
239 查看
在上一节中,我们对支持向量机(SVM)有了一个大概的印象,当然,这还远远不够。在深入了解之前,在本节中我们将涉及分类问题。分类的目的是学会一个分类函数或分类模型(或者叫做分类器),该模型能将数据库中的数据项映射到给定类别中的某一个,从而可以用于预测未知类别。分类在机器学习、数据挖掘等领域中得到广泛的应用,可以用来解决各种实际应用问题,因此它的重要性不言而喻。
支持向量机(SVM)算法也是分类方法的一种。
wTx+b=0wTx+b=0
这个1或–1的分类标准起源于逻辑回归,下面进行介绍。
hθ(x)=g(θTx)(1.1)(1.1)hθ(x)=g(θTx)
其中 xx 是 nn 维特征向量,函数 gg 就是逻辑函数。对于一元变量的情形,g(z)=11+e−zg(z)=11+e−z 的图像为:
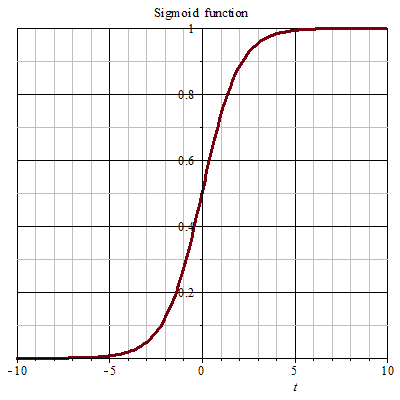
由上图可以看出,函数gg将(−∞,+∞)(−∞,+∞)映射到了 (0,1)(0,1),式 (1.1)(1.1) 可作为 xx 对应 y=1y=1 的概率:
P{y=1|x;θ}=hθ(x)(1.2)(1.2)P{y=1|x;θ}=hθ(x)
P{y=0|x;θ}=1−hθ(x)(1.3)(1.3)P{y=0|x;θ}=1−hθ(x)
如果要判别一个数据点 xx 属于哪个类时,只需求 hθ(x)hθ(x),若大于 0.50.5 就是 y=1y=1 的类,反之属于 y=0y=0 类,也即自变量 θTxθTx 若大于 00 就是 y=1y=1 的类,否则属于 y=0y=0 类。
总结:逻辑回归就是要学习得到 θθ,使得正例的特征远大于 00,负例的特征远小于 00,强调在全部训练实例上达到这个目标。
扩展:分类与回归的区别是什么?
答:区别在于输出变量的类型。
定量输出称为回归,或者说是连续变量预测;
定性输出称为分类,或者说是离散变量预测。
*举个例子:
预测明天的气温是多少度,这是一个回归任务;
预测明天是阴、晴还是雨,就是一个分类任务。*
现在,我们可以把式 (1.1)(1.1) 重写为:
hw,b(x)=g(wT+b)(1.4)(1.4)hw,b(x)=g(wT+b)
“逻辑回归”部分提到过:只需考虑 θTxθTx 的正负问题,而不用关心 g(z)g(z),因此我们这里将 g(z)g(z) 做一个简化,将其简单映射到 y=−1和y=1y=−1和y=1 上。映射关系如下:
g(z)={1,−1,if z≥0if z<0(1.5)(1.5)g(z)={1,if z≥0−1,if z<0
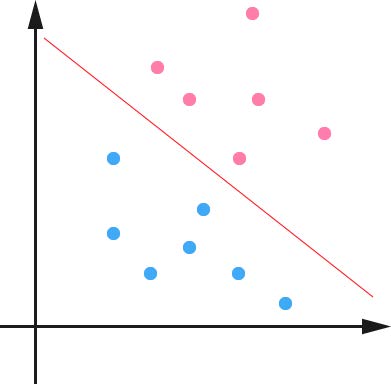
图中粉红色的线(即木棍)将红蓝色的点(即红蓝小球)分开,这条线也称为超平面(hyperplane),也可以说,在超平面一边的数据点所对应的 yy 全是 –1–1,而在另一边全是 11。
设分类函数(重要:后面会重点讨论)为:
f(x)=wTx+b(1.6)(1.6)f(x)=wTx+b
显然,如果 f(x)=0f(x)=0,那么 xx 是位于超平面上的点。我们不妨要求对于所有满足 f(x)<0f(x)<0 的点,其对应的 yy 等于 –1–1,而 f(x)>0f(x)>0 则对应 y=1y=1 的数据点,见下图。
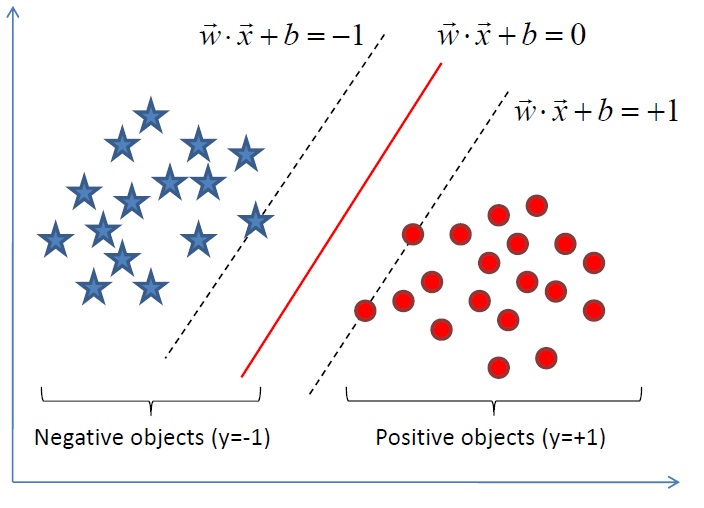
我们先从最简单的情形开始,假设数据都是线性可分的,亦即这样的超平面是存在的。当然,有些时候,或者说大部分时候数据并不是线性可分的,这个时候满足这样条件的超平面就根本不存在(后面会涉及到)。
再实际应用中,我们在进行分类的时候,将数据点 xx 代入 f(x)f(x) 中,如果得到的结果小于 00,则赋予其类别 –1–1,如果大于 00 则赋予类别 11。如果 f(x)=0f(x)=0,则会出现问题,它并不属于任何一类。
[2]分类与回归区别是什么? - 走刀口的回答 - 知乎
更多机器学习干货、最新论文解读、AI资讯热点等欢迎关注“AI学院(FAICULTY)”,内容持续更新中……
欢迎加入faiculty机器学习交流qq群:451429116(点此进群)
版权声明:本文不可任意转载,转载请联系作者。
支持向量机(SVM)算法也是分类方法的一种。
线性二分类模型
分类标准
对于两类分类问题,将数据点用 xx 来表示,这是一个 nn 维向量,wTwT 上标中的“TT”代表转置,而类别用 yy 来表示,可以取 11 或者 –1–1,分别代表两个不同的类。一个线性分类器就是要在 nn 维的数据空间中找到一个超平面,其方程可以表示为:wTx+b=0wTx+b=0
这个1或–1的分类标准起源于逻辑回归,下面进行介绍。
逻辑回归
逻辑回归(Logistic Regression)的目的是从特征学习出一个 0/10/1 分类模型,而这个模型是将特征的线性组合作为自变量,由于自变量的取值范围是负无穷到正无穷。因此,使用逻辑函数(或称作Sigmoid函数)将自变量映射到 (0,1)(0,1) 上,映射后的值被认为是属于 y=1y=1 的概率。形式化表示就是:假设函数hθ(x)=g(θTx)(1.1)(1.1)hθ(x)=g(θTx)
其中 xx 是 nn 维特征向量,函数 gg 就是逻辑函数。对于一元变量的情形,g(z)=11+e−zg(z)=11+e−z 的图像为:

由上图可以看出,函数gg将(−∞,+∞)(−∞,+∞)映射到了 (0,1)(0,1),式 (1.1)(1.1) 可作为 xx 对应 y=1y=1 的概率:
P{y=1|x;θ}=hθ(x)(1.2)(1.2)P{y=1|x;θ}=hθ(x)
P{y=0|x;θ}=1−hθ(x)(1.3)(1.3)P{y=0|x;θ}=1−hθ(x)
如果要判别一个数据点 xx 属于哪个类时,只需求 hθ(x)hθ(x),若大于 0.50.5 就是 y=1y=1 的类,反之属于 y=0y=0 类,也即自变量 θTxθTx 若大于 00 就是 y=1y=1 的类,否则属于 y=0y=0 类。
总结:逻辑回归就是要学习得到 θθ,使得正例的特征远大于 00,负例的特征远小于 00,强调在全部训练实例上达到这个目标。
扩展:分类与回归的区别是什么?
答:区别在于输出变量的类型。
定量输出称为回归,或者说是连续变量预测;
定性输出称为分类,或者说是离散变量预测。
*举个例子:
预测明天的气温是多少度,这是一个回归任务;
预测明天是阴、晴还是雨,就是一个分类任务。*
形式化表示
我们采用结果标签 y=−1y=−1 和 y=1y=1,分别替换在逻辑回归中使用的y=0y=0 和 y=1y=1。同时将 θθ 替换成 ww 和 bb。以前的 θTx=θ0+θ1x1+θ2x2+…+θnxnθTx=θ0+θ1x1+θ2x2+…+θnxn(其中认为 x0=1x0=1)。现在我们替换 θ0θ0 为 bb,替换后面的 θ1x1+θ2x2+…+θnxnθ1x1+θ2x2+…+θnxn 为 w1x1+w2x2+…+wnxnw1x1+w2x2+…+wnxn(即 wTxwTx)。这样,我们让 θTx=wTx+bθTx=wTx+b,进一步 hθ(x)=g(θTx)=g(wTx+b)hθ(x)=g(θTx)=g(wTx+b)。也就是说除了 yy 由 y=0y=0 变为y=−1y=−1,只是标签表示值不同外,与逻辑回归的形式化表示没有区别。现在,我们可以把式 (1.1)(1.1) 重写为:
hw,b(x)=g(wT+b)(1.4)(1.4)hw,b(x)=g(wT+b)
“逻辑回归”部分提到过:只需考虑 θTxθTx 的正负问题,而不用关心 g(z)g(z),因此我们这里将 g(z)g(z) 做一个简化,将其简单映射到 y=−1和y=1y=−1和y=1 上。映射关系如下:
g(z)={1,−1,if z≥0if z<0(1.5)(1.5)g(z)={1,if z≥0−1,if z<0
线性分类举例
还记得上一节桌面上用木棍分开红蓝小球的例子嘛?将其抽象到二维平面上表示为:
图中粉红色的线(即木棍)将红蓝色的点(即红蓝小球)分开,这条线也称为超平面(hyperplane),也可以说,在超平面一边的数据点所对应的 yy 全是 –1–1,而在另一边全是 11。
设分类函数(重要:后面会重点讨论)为:
f(x)=wTx+b(1.6)(1.6)f(x)=wTx+b
显然,如果 f(x)=0f(x)=0,那么 xx 是位于超平面上的点。我们不妨要求对于所有满足 f(x)<0f(x)<0 的点,其对应的 yy 等于 –1–1,而 f(x)>0f(x)>0 则对应 y=1y=1 的数据点,见下图。

我们先从最简单的情形开始,假设数据都是线性可分的,亦即这样的超平面是存在的。当然,有些时候,或者说大部分时候数据并不是线性可分的,这个时候满足这样条件的超平面就根本不存在(后面会涉及到)。
再实际应用中,我们在进行分类的时候,将数据点 xx 代入 f(x)f(x) 中,如果得到的结果小于 00,则赋予其类别 –1–1,如果大于 00 则赋予类别 11。如果 f(x)=0f(x)=0,则会出现问题,它并不属于任何一类。
参考文献
[1]支持向量机通俗导论(理解SVM的三层境界) - July[2]分类与回归区别是什么? - 走刀口的回答 - 知乎
更多机器学习干货、最新论文解读、AI资讯热点等欢迎关注“AI学院(FAICULTY)”,内容持续更新中……
欢迎加入faiculty机器学习交流qq群:451429116(点此进群)
版权声明:本文不可任意转载,转载请联系作者。
相关文章推荐
- 采用线性SVM对线性不可分的数据进行分类(含matlab实现)
- 深度学习与计算机视觉系列(3)_线性SVM与SoftMax分类器
- 线性鉴别分析(LDA)之二分类问题
- 分类算法----线性可分支持向量机(SVM)算法的原理推导
- spark Mllib基本功系列编程入门之 SVM实现分类
- eclipse + libsvm-3.12 用SVM实现简单线性分类
- 用tensorflow实现svm的线性和非线性分类
- 深度学习与计算机视觉系列(3)_线性SVM与SoftMax分类器
- svm入门之二、三线性分类器
- HDU 2042 不容易系列之二 [补6.24] 分类: ACM 2015-06-26 20:40 9人阅读 评论(0) 收藏
- 支持向量机——线性分类SVM
- 深度学习与计算机视觉系列(3)_线性SVM与SoftMax分类器
- 转载SVM讲解一(线性分类)
- DNS扫盲系列之二:域名解析及DNS功能分类
- 【Python学习系列八】Python实现线性可分SVM(支持向量机)
- 深度学习与计算机视觉系列(3)_线性SVM与SoftMax分类器
- eclipse + libsvm-3.12 用SVM实现简单线性分类
- 深度学习与计算机视觉系列(3)_线性SVM与SoftMax分类器
- python SVM调包线性分类西瓜
- SVM边学边总结系列——线性不可分情况
