HDU 1695 GCD 【莫比乌斯入门】
2018-01-22 23:00
274 查看
不懂的莫比乌斯的请详细看看这篇博客, 讲的非常好!!!
传送门
// 就是求有多少对(x, y) 满足 GCD(x, y) == k , 其中 1 <= x <= c, 1 <= y <= d. 注意题目最后的一句话(你可以认为所有case中的区间的开头是1)
// 我们首先对问题进行转化, 可以变成求GCD(x/k, y/k) == 1. 所以
这个就是莫比乌斯的裸题啦~ 根据上面的那个博客所讲的知识我们做如下假设
设G(n) 表示 有多少对(x, y) 满足 GCD(x, y) == n 的倍数(即有多少对(x, y) % n == 0), 那么同理我们就有F(n) 代表 有多少对(x, y) 满足GCD(x, y) == n, 所以我们题目的要求就是求F(1) , 然后根据莫比乌斯的(有两种形式)第二种形式我们可以知道F(1) = sigma(U(i) * G(i)) ( 1 <= i <= N), 然后对于G(n) 我们又容斥定理可以得到 = (a/n)*(b/n) 的, N = min(a, b);
所以我们要求的答案就转化为了 F(1) = U(1) * (a)(b) + U(2) (a/2)(b/2) +….+ U(i) (a/i)*(b/i), 其中U(i)表示i的莫比乌斯函数(不懂的建议看看我在最上面附上的链接). 附上一个nlogn求莫比乌斯的程序.
还有就是题目中说了(1, 2) 和 (2, 1) 算一种, 所以我们应该减去重复的, 重复的具体在哪里了, 其实就是最小的范围里的那一坨. 借用其他博客的一张图说明:
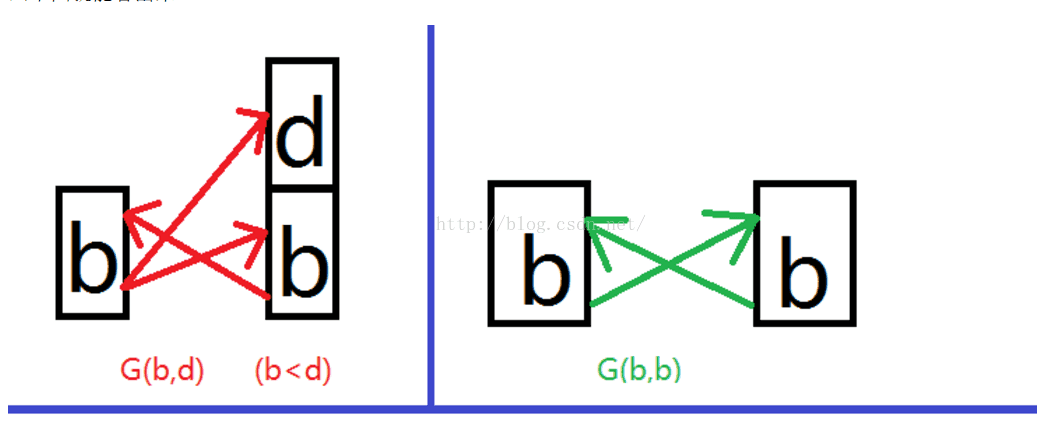
即大于b的那一部分是没有重合的. 即 G(b,d)- G(b,b)/ 2 就是最终我们要求的结果了.
所以本题的AC 代码就可以给出了
AC Code
肯定还是有疑问的, 怎么想到设这两个函数的, 我这说下, 首先给出重用的两种莫比乌斯函数的形式
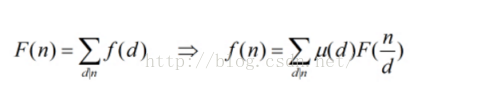
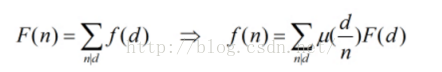
很明显的可以看出两者的不同, 前者是约数关系, 后者是倍数关系, 而且也只有满足了这两种关系后才能用莫比乌斯函数进行转化, 所以对于一道题如果感觉像用莫比乌斯来做, 那么构造函数时就应该尽量的往这方面来靠.
终究还是必须得做题做的多才行.
传送门
// 就是求有多少对(x, y) 满足 GCD(x, y) == k , 其中 1 <= x <= c, 1 <= y <= d. 注意题目最后的一句话(你可以认为所有case中的区间的开头是1)
// 我们首先对问题进行转化, 可以变成求GCD(x/k, y/k) == 1. 所以
这个就是莫比乌斯的裸题啦~ 根据上面的那个博客所讲的知识我们做如下假设
设G(n) 表示 有多少对(x, y) 满足 GCD(x, y) == n 的倍数(即有多少对(x, y) % n == 0), 那么同理我们就有F(n) 代表 有多少对(x, y) 满足GCD(x, y) == n, 所以我们题目的要求就是求F(1) , 然后根据莫比乌斯的(有两种形式)第二种形式我们可以知道F(1) = sigma(U(i) * G(i)) ( 1 <= i <= N), 然后对于G(n) 我们又容斥定理可以得到 = (a/n)*(b/n) 的, N = min(a, b);
所以我们要求的答案就转化为了 F(1) = U(1) * (a)(b) + U(2) (a/2)(b/2) +….+ U(i) (a/i)*(b/i), 其中U(i)表示i的莫比乌斯函数(不懂的建议看看我在最上面附上的链接). 附上一个nlogn求莫比乌斯的程序.
int mu[maxn];
void getmu(int n) {
for (int i = 1 ; i <= n ; i ++) {
int x = i == 1 ? 1 : 0;
int y = x - mu[i];
mu[i] = y;
for (int j = i+i ; j <= n ; j += i) {
mu[j] += y;
}
}
}还有就是题目中说了(1, 2) 和 (2, 1) 算一种, 所以我们应该减去重复的, 重复的具体在哪里了, 其实就是最小的范围里的那一坨. 借用其他博客的一张图说明:

即大于b的那一部分是没有重合的. 即 G(b,d)- G(b,b)/ 2 就是最终我们要求的结果了.
所以本题的AC 代码就可以给出了
AC Code
const int maxn = 1e5+5;
int mu[maxn]; // 放在case的最外面进行初始化就行啦.
void getmu(int n) {
for (int i = 1 ; i <= n ; i ++) {
int x = i == 1 ? 1 : 0;
int y = x - mu[i];
mu[i] = y;
for (int j = i+i ; j <= n ; j += i) {
mu[j] += y;
}
}
}
void solve()
{
int a,b,c,d,k;
cin >> a >> c >> b >> d >> k;
if (!k) {
cout << 0 << endl;
return ;
}
c /= k , d /= k;
ll ans1 = 0 , ans2 = 0;
for (int i = 1 ; i <= min(c, d) ; i ++) {
ans1 += 1ll*mu[i]*(c/i)*(d/i);
}
for (int i = 1 ; i <= min(c, d) ; i ++) {
ans2 += 1ll*mu[i]*(min(c, d)/i)*(min(c, d)/i);
}
cout << ans1 - ans2/2 << endl;
}肯定还是有疑问的, 怎么想到设这两个函数的, 我这说下, 首先给出重用的两种莫比乌斯函数的形式
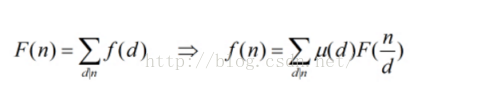
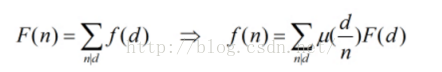
很明显的可以看出两者的不同, 前者是约数关系, 后者是倍数关系, 而且也只有满足了这两种关系后才能用莫比乌斯函数进行转化, 所以对于一道题如果感觉像用莫比乌斯来做, 那么构造函数时就应该尽量的往这方面来靠.
终究还是必须得做题做的多才行.
相关文章推荐
- HDU 1695 GCD (莫比乌斯反演入门学习小结)
- 【数论-莫比乌斯入门】hdu 1695 GCD
- HDU 1695 GCD(莫比乌斯反演,入门)
- HDU 1695 GCD【莫比乌斯反演】
- hdu 1695 GCD 欧拉函数+容斥 ||莫比乌斯反演
- hdu 1695 GCD(莫比乌斯反演+分块模板)
- HDU - 1695 GCD 莫比乌斯反演
- hdu 1695 GCD(莫比乌斯)
- hdu 1695 GCD 莫比乌斯
- HDU1695 GCD 数论之 莫比乌斯反演
- HDU 莫比乌斯反演 1695 GCD
- hdu 1695 莫比乌斯反演入门题
- HDU 1695 GCD [莫比乌斯反演]
- HDU 1695 GCD 欧拉函数+容斥定理 || 莫比乌斯反演
- hdu 1695 GCD(莫比乌斯反演入门)
- HDU 1695 GCD 莫比乌斯,容斥原理
- HDU 1695 GCD (容斥 + 莫比乌斯反演)
- hdu 1695: GCD 【莫比乌斯反演】
- HDU 1695 GCD (容斥原理+欧拉函数)
- HDU_1695_GCD(欧拉函数+容斥原理+DFS)
