【图】最小生成树(最小成本):克鲁斯卡尔(Kruskal)算法
2018-01-19 11:09
411 查看
给出一个连通网:
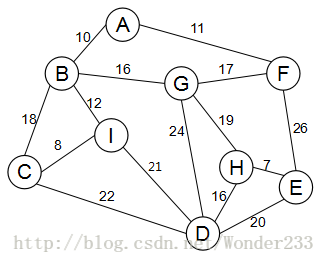
令最小生成树的初始状态为只有 n 个顶点并且没有边的非连通图 T={V,{}} ,图中每个顶点自成一个连通分量。
在 E 中选择代价最小的边,若该边的两个顶点落在 T 中不同的连通分量上,则将此边加入到 T 中,否则就舍去此边而选择下一条代价最小的边。
以此类推,直至 T 中所有顶点都在同一连通分量上为止。
克鲁斯卡尔算法主要针对边来展开,边数少时效率会非常高,所以对稀疏图有很大的优势;
而普里姆算法对于稠密图,即边数非常多的情况会更好一些。

2、去掉所有边,得到 T={A,B,C,D,E,F,G,H,I,{}}。
3、对边集数组做循环遍历,开始时,i=0,找到第 1 条边,两顶点为 E 与 H,分别属于两棵树(两个连通分量),所以添加进 T={A,B,C,D,E,F,G,H,I,{(E,H)}}。


4、i=1,找到第 2 条边,两顶点为 C 与 I,分别属于两棵树(两个连通分量),所以添加进 T={A,B,C,D,E,F,G,H,I,{(E,H),(C,I)}}。
5、i=2,找到第 3 条边,两顶点为 A 与 B,分别属于两棵树(两个连通分量),所以添加进 T={A,B,C,D,E,F,G,H,I,{(E,H),(C,I),(A,B)}}。


6、i=3,找到第 4 条边,两顶点为 A 与 F,分别属于两棵树(两个连通分量),所以添加进 T={A,B,C,D,E,F,G,H,I,{(E,H),(C,I),(A,B),(A,F)}}
7、i=4,找到第 5 条边,两顶点为 B 与 I,分别属于两棵树(两个连通分量),所以添加进 T={A,B,C,D,E,F,G,H,I,{(E,H),(C,I),(A,B),(A,F),(B,I)}}


8、i=5,找到第 6 条边,两顶点为 D 与 H,分别属于两棵树(两个连通分量),所以添加进 T={A,B,C,D,E,F,G,H,I,{(E,H),(C,I),(A,B),(A,F),(B,I),(D,H)}}
9、i=6,找到第 7 条边,两顶点为 B 与 G,分别属于两棵树(两个连通分量),所以添加进 T={A,B,C,D,E,F,G,H,I,{(E,H),(C,I),(A,B),(A,F),(B,I),(D,H),(B,G)}}


10、i=7,找到第 8 条边,两顶点为 G 与 F,它们属于同一棵树,舍去。再找 i=8,两顶点为 B 与 C,它们属于同一棵树,舍去。再找 i=9,两顶点为 G 与 H,分别属于两棵树(两个连通分量),所以添加进 T={A,B,C,D,E,F,G,H,I,{(E,H),(C,I),(A,B),(A,F),(B,I),(D,H),(B,G),(G,H)}}。
11、此后的循环均造成环路,最终最小生成树如下。


克鲁斯卡尔(Kruskal)算法
基本思想
假设 N=(V,{E}) 是连通网:令最小生成树的初始状态为只有 n 个顶点并且没有边的非连通图 T={V,{}} ,图中每个顶点自成一个连通分量。
在 E 中选择代价最小的边,若该边的两个顶点落在 T 中不同的连通分量上,则将此边加入到 T 中,否则就舍去此边而选择下一条代价最小的边。
以此类推,直至 T 中所有顶点都在同一连通分量上为止。
克鲁斯卡尔算法主要针对边来展开,边数少时效率会非常高,所以对稀疏图有很大的优势;
而普里姆算法对于稠密图,即边数非常多的情况会更好一些。
图解
1、将连通网中的边转化为边集数组,并对它们按权值从小到大排序。
2、去掉所有边,得到 T={A,B,C,D,E,F,G,H,I,{}}。
3、对边集数组做循环遍历,开始时,i=0,找到第 1 条边,两顶点为 E 与 H,分别属于两棵树(两个连通分量),所以添加进 T={A,B,C,D,E,F,G,H,I,{(E,H)}}。


4、i=1,找到第 2 条边,两顶点为 C 与 I,分别属于两棵树(两个连通分量),所以添加进 T={A,B,C,D,E,F,G,H,I,{(E,H),(C,I)}}。
5、i=2,找到第 3 条边,两顶点为 A 与 B,分别属于两棵树(两个连通分量),所以添加进 T={A,B,C,D,E,F,G,H,I,{(E,H),(C,I),(A,B)}}。


6、i=3,找到第 4 条边,两顶点为 A 与 F,分别属于两棵树(两个连通分量),所以添加进 T={A,B,C,D,E,F,G,H,I,{(E,H),(C,I),(A,B),(A,F)}}
7、i=4,找到第 5 条边,两顶点为 B 与 I,分别属于两棵树(两个连通分量),所以添加进 T={A,B,C,D,E,F,G,H,I,{(E,H),(C,I),(A,B),(A,F),(B,I)}}


8、i=5,找到第 6 条边,两顶点为 D 与 H,分别属于两棵树(两个连通分量),所以添加进 T={A,B,C,D,E,F,G,H,I,{(E,H),(C,I),(A,B),(A,F),(B,I),(D,H)}}
9、i=6,找到第 7 条边,两顶点为 B 与 G,分别属于两棵树(两个连通分量),所以添加进 T={A,B,C,D,E,F,G,H,I,{(E,H),(C,I),(A,B),(A,F),(B,I),(D,H),(B,G)}}


10、i=7,找到第 8 条边,两顶点为 G 与 F,它们属于同一棵树,舍去。再找 i=8,两顶点为 B 与 C,它们属于同一棵树,舍去。再找 i=9,两顶点为 G 与 H,分别属于两棵树(两个连通分量),所以添加进 T={A,B,C,D,E,F,G,H,I,{(E,H),(C,I),(A,B),(A,F),(B,I),(D,H),(B,G),(G,H)}}。
11、此后的循环均造成环路,最终最小生成树如下。

时间复杂度
找边的两顶点是否属于同一棵树的时间复杂度为 O(loge),而外面有一个 for 循环 e 次。所以克鲁斯卡尔算法的时间复杂度为 O(eloge)(e 表示边的条数)。相关文章推荐
- 数据结构之---C语言实现最小生成树之kruskal(克鲁斯卡尔)算法
- 最小生成树(MST)----普里姆(Prim)算法与克鲁斯卡尔(Kruskal)算法
- MST最小生成树及克鲁斯卡尔(Kruskal)算法
- 图论中最小生成树算法-Prim(普里姆)算法、kruskal(克鲁斯卡尔避圈法)算法、破圈算法
- java实现图的最小生成树(森林)MST克鲁斯卡尔(Kruskal)算法
- 关于最小生成树中的 Kruskal(克鲁斯卡尔)算法
- 最小生成树——克鲁斯卡尔(Kruskal)算法
- 图论之最小生成树-----克鲁斯卡尔(Kruskal)算法
- 最小生成树之克鲁斯卡尔(Kruskal)算法实现,代码详解!!!!
- 最小生成树问题(Kruskal 算法)(克鲁斯卡尔)
- 最小生成树——Kruskal(克鲁斯卡尔)算法
- 最小生成树(qsort+并查集+克鲁斯卡尔(Kruskal)算法)
- 算法:图解最小生成树之克鲁斯卡尔(Kruskal)算法
- 最小生成树之Kruskal(克鲁斯卡尔)算法
- 最小生成树的克鲁斯卡尔(kruskal)算法
- 图解最小生成树 - 克鲁斯卡尔(Kruskal)算法
- 最小生成树——Kruskal(克鲁斯卡尔)算法
- 最小生成树 Kruskal(克鲁斯卡尔)算法
- 第十三周 最小生成树的克鲁斯卡尔(Kruskal)算法
- 最小生成树算法(下)——Kruskal(克鲁斯卡尔)算法
