python机器学习案例系列教程——逻辑分类/逻辑回归LR/一般线性回归(softmax回归)
2018-01-03 09:04
1076 查看
全栈工程师开发手册 (作者:栾鹏)
python数据挖掘系列教程
逻辑分类(Logistic Classification)是一种线性模型,可以表示为y=f(w∗x+b),其中w是训练得到的权重参数(Weight);x是样本特征数据;b是偏置(Bias),f成为激活函数。
就是给定一批样本数据集,和样本对象所属的分类,进行建立模型。使用模型对新来的对象对象分类预测。
值得注意的是,逻辑分类中,我们想要的结果为分类类型,而不再是线性回归中的数值。
注意:在逻辑分类中,我们想要的结果是对象所属的分类,比如A类、B类,属于标称型数据。但是在数学中,一般没办法使用A、B表示,而使用0、1、2、3表示每种类别。注意这里的0、1、2、3只是表示对应的标称分类,并不表示具体的数值。也就是说,并不能表述为1比0大,就像不能表述为B类比A类大。也不能表述为1比3更靠近0,就像不能表述为B类比C类更靠近A类。必能在逻辑分类的学习中,一定要注意把握这一点。
既然逻辑分类中,我们想要的输出结果不再是数值型的,但是在线性回归中我们学习的都是计算数值型的结果,那怎么应用呢?
我们可以使用一种成为one-hot编码的方式,将分类编码成数值。
比如有4个分类0、1、2、3。我们可以将
分类0编码成[1,0,0,0] 第一个分量的值为1,其他为0,表示为对象属于第一个分类的概率为1,属于其他分类的概率为0。
分类1编码成[0,1,0,0] 第二个分量的值为1,其他为0,表示为对象属于第二个分类的概率为1,属于其他分类的概率为0。
分类2编码成[0,0,1,0] 第三个分量的值为1,其他为0,表示为对象属于第三个分类的概率为1,属于其他分类的概率为0。
分类3编码成[0,0,0,1] 第四个分量的值为1,其他为0,表示为对象属于第四个分类的概率为1,属于其他分类的概率为0。
而分类概率是数值型的,也就是说我们预测的结果就变成了四维数值型的。
比如下面是你拿到的数据集。第一列为属性x1,第二列为属性x2,第三列为分类结果,包含0,1,2三种分类
必须先将数据集转化为下面的模式。x0为常值0,对象的回归系数表示偏量值b,标称型分为转化为数值型概率。
这样我们要求的回归系数矩阵w也不再是线性回归中的向量,而是矩阵。
比如
有m行x,每一个x有n个属性,然后每个x有一个分类,也就有m行y,每个y可以被分成k个元素的向量,我需要先把m行y变成一个m行k列的矩阵,最后计算出一个(j+1)*k列的w矩阵。
线性回归就是计算回归系数,通过回归系数线性组合属性预测数值结果。
线性回归以误差平方和最小为目的,其实是在假定误差服从高斯分布
f(x)=wx+b
二分类的线性分类:
在线性回归的基础上添加了大于和小于0的判断。当值大于0属于一种分类,当值小于0等于另一种分类。
f(n)={1,−1,f(x) ≥ 0f(x)<0
逻辑回归:
逻辑回归是逻辑分类的一种。
逻辑分类为
y=f(w∗x+b)
当f函数为sigmoid函数时,就是逻辑回归。即
y=sigmoid(w∗x+b)
逻辑回归就是在线性回归的基础上,再经过sigmoid这个非线性函数,将值转化为分类的概率。 逻辑回归实际上是采用的是 伯努利分布来分析误差。
sigmoid函数:
sigmoid(x)=11+e−x

逻辑分类:
逻辑分类属于线性模型。逻辑分类包含逻辑回归、一般线性回归。逻辑回归为二分类问题,一般线性回归为多分类问题。
二分类:在逻辑回归的基础上,判断分类概率是否大于0.5,大于则属于这个分类。
y={1,−1,f(wx+b) ≥ 0.5f(wx+b)<0.5
而由于sigmoid函数是单调的,当sigmoid的输入为0时,输出为0.5,所以等价于逻辑回归二分类的判别为以下公式,这与线性分类的公式相同。
wx+b=0
多分类:一般线性回归:
高斯分布、伯努利分布、贝塔分布、迪特里特分布,都属于指数分布。所以一般线性回归就是用指数分布来处理噪声模型的方法。一般使用softmax函数来处理多分类问题。softmax回归是一般线性回归的一个例子。
f(wx+b)=softmax(wx+b)
softmax函数
softmax函数其实就是一个归一化的指数函数
softmax(x)=exi∑iexi
在使用一般线性回归进行分类中,计算哪个分类的概率大就属于哪个分类。
在逻辑分类中,类别给ont-hot编码为概率。在统计学上,衡量两个概率的分布向量的差异程度,叫做交叉熵(Cross Entropy),
交叉熵函数如下:
D(y,p)=yln(p)+(1−y)(1−ln(p)) 其中p=softmax(wx+b)
逻辑分类中的损失函数为
loss(w,b)=−1/m∑D(yi,pi)
线性回归为估值预测而生,逻辑分类为分类预测而生。
下面为线性回归和逻辑分类的模型示例。
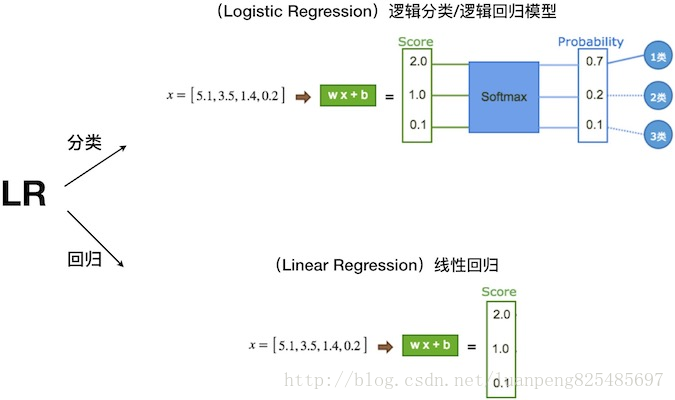
逻辑分类是一个包含线性和非线性部分用来进行分类的分类器。我们以n分类为例进行分析。
假设已经知道回归系数矩阵w和偏量b,逻辑分类包含下面的3个步骤。
1、计算线性函数的输出值
根据输入对象x和已知的回归系数矩阵w,以及偏量b,计算输入经过线性函数后的输出值,即h=wx+b。输出值h也是n维的。每一维可以近似认为是待测对象偏向于每种分类的成分。
2、将线性函数的输出结果转化为分类概率
得到了线性函数的输出结果,还需要将每一个维度转化为对象属于每个分类的概率。使得每个概率在0-1之间。这是一步非线性操作,所以这一步不再属于线性回归的范围。
将输出结果转化为概率的函数我们称为阶跃函数,也叫做激活函数。
一般在神经网络中用的最多的是sigmoid和tanh,当然也有用relu的。这是针对“是”和“否”的分类,但当进行多分类时,就要用到softmax 。
如果使用sigmoid函数进行二分类,sigmoid函数的功能在于:
sigmoid(x)=11+e−x
1、将线性函数的输出向量作为输入的“分数”,将“分数”映射在(0,1)之间。
2、以“对数”的方式完成到(0,1)的映射,凸显大的分数的作用,使其输出的概率更高,抑制小分数的输出概率。
如果使用softmax函数进行多分类,softmax函数的功能在于:
softmax(x)=exi∑iexi
1、将线性函数的输出向量作为输入的“分数”,将“分数”映射在(0,1)之间,并且所有分数的和为1。
2、以“对数”的方式完成到(0,1)的映射,凸显其中最大的分数的作用,并抑制远低于最大分数的其他数值。
我们使用代码来看看softmax的效果。
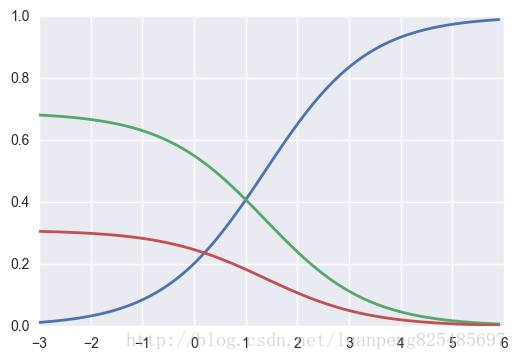
输出:
根据输出结果我们可以看出,当softmax的输入值被方法100倍时,数值之间的差距被拉大。softmax对这种差距敏感,差距越大,分类器越‘自信’,差距越小,分类器越‘犹豫’。
3、将分类概率转化为类别
这一步就比较简单了,当属于某分类的概率最大时,就可以判定为数据该分类。
那如何求解正确的回归系数w和偏量b呢,因为只有有了正确的w和b,才能带入逻辑分类公式进行分类判别。
(后面的教程就省略b偏量,因为b偏量可以认为是样本一个值为1 的属性对应的权重)
线性函数g部分我们表示为:
g(X)=XW
逻辑回归的激活函数f部分我们表示为:
f(z)=sigmoid(z)
softmax回归的激活函数f部分表示为:
f(z)=softmax(z)
当然我们也可以直接将输入x表示为最终的输出结果
y=h(x)=f(z)=f(g(x))=f(xw)
在线性回归中,我们学习了线性回归的梯度下降法和随机梯度下降法,在逻辑回归、甚至以后的神经网络、全连接神经网络、卷积神经网络、循环神经网络都是使用梯度下降法(随机梯度下降法)来进行后向传播算法实现回归系数w或网络层系数w的迭代收敛计算。
梯度下降法的步骤(线性回归、逻辑回归、所有的神经网络都是相同的步骤):
1、写出损失函数。
2、损失函数对自变量w求导,得到w的梯度。
3、根据梯度,更细w权重。
梯度下降法求解的是使损失函数(误差平方和)最小的权重矩阵w。
误差平方和为
J(w)=∑mi=1(xiw−yi)2
对w求导的得到梯度
∇J(w)=2XT(Xw−y)
回归系数更新
wk+1=wk−ρ∗∇J(wk)=wk−ρ∗2XT(Xwk−y)
我们来按照这个步骤解决逻辑回归中的梯度下降。
一般定义逻辑回归的损失函数为
J(w)=−1m∑mi=1[yiloghw(xi)+(1−yi)log(1−hw(xi))]
其中
x(i) 每个样本数据点在某一个特征上的值,即样本对象x的某个属性的值
y(i) 每个样本数据的所属类别标签
m 样本数据点的个数
hw(x) 样本数据的概率密度函数,即某个数据属于1类(二分类问题)的概率
J(w) 代价函数,估计样本属于某类的风险程度,越小代表越有可能属于这类这个
这个损失函数是按照求最大似然函数的方法,求得逻辑回归似然函数后再取对数形成的,喜欢公式的朋友们可以移步http://blog.csdn.net/lookqlp/article/details/51161640
不喜欢公司也没必要记住这个公式,只需要记住下面的w梯度和w更新公式就行。
对损失函数求导得到w的梯度为
∇J(w)=∑mi=1xTi∗(f(xiw)−yi)=XT(f(Xw)−y)=XT(sigmoid(Xw)−y)
其中xi表示第i个样本对象(行向量),yi表示第i个输出结果(行向量),f为激活函数,X为m个样本数据集,每行为一个对象,y为m个输出结果。
再强调一遍,在线性回归中我们一般使用的案例都是预测一个数值型数据,在逻辑回归中代表分类的数字并不是数值型的,所以经过one-hot编码后变成了多个数值型的输出结果。
所以在逻辑回归中,梯度下降法的更新公式为
wk+1=wk−ρ∇J(wk)=wk−ρXT(sigmoid(Xwk)−y)
在有些教程中,喜欢用列向量表示一个样本对象x,则一个对象的输出结果y也是列向量。你看到的逻辑回归的梯度写法不相同,不过不用慌张,它只是数据的行列形式不同罢了。
我们来按照这个步骤解决softmax回归中的梯度下降。
喜欢公式的可以移步https://www.cnblogs.com/Determined22/p/6362951.html
我们只对softmax回归的结果给出。
在softmax回归中,梯度下降法的更新公式为
wk+1=wk−ρ∇J(wk)=wk−ρXT(softmax(Xwk)−y)
所以说线性回归、逻辑回归、softmax回归的梯度更新公式都是一样的。
在线性回归中回归系数的更新如下,其中xk为第k个样本对象(行向量)。yk为该对象输出的结果,为数值。
wk+1=wk−2∗ρkxTk(xkwk−yk)
在逻辑回归中,每个对象的输出结果(类别)被one-hot编码成向量,随机梯度下降法的更新公式为
wk+1=wk−ρkxTk(sigmoid(xkwk)−yk)
其中xk为一个样本对象(行向量),yk为该对象的输出(行向量)。
在softmax回归中,随机梯度下降法的更新公式为
wk+1=wk−ρkxTk(softmax(xkwk)−yk)
喜欢数学推导的朋友可以自己去百度,这里就不给出了。
先将数据集转化为逻辑分类可以处理的数据结构。即,为对象添加值为1的属性x0,将输出分类转换为one-hot编码。
我们先来看看数据是个什么样子
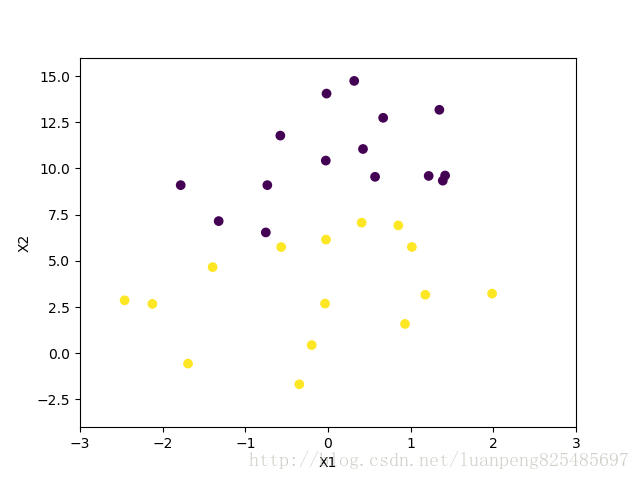
我们使用的样本数据,有两个特征属性,x1和x2如果,算上b偏量就是三个回归系数。结果为2分类。
则线性函数的输出结果为[z0,z1]
z0=w00*1 + w01*x1 + w02*x2
z1=w10*1 + w11*x1 + w12*x2
线性函数的结果[z0,z1]再经过Sigmoid激活函数,可得到预测的分类概率[y0,y1]。当然最开始这个预测的分类概率并不准确,所以需要模型训练,不停的根据预测的结果是否准确来调整回归系数。
其中Sigmoid逻辑回归函数实现如下:
wk+1=wk−ρ∇J(wk)=wk−ρXT(sigmoid(Xwk)−y)
按照这个公式实现代码
绘制分类区域
回归系数矩阵w为:
[[-25.38603398 25.43723638]
[ -3.98349475 3.99351765]
[ 3.60847635 -3.61579463]]
绘制出的分割区域为
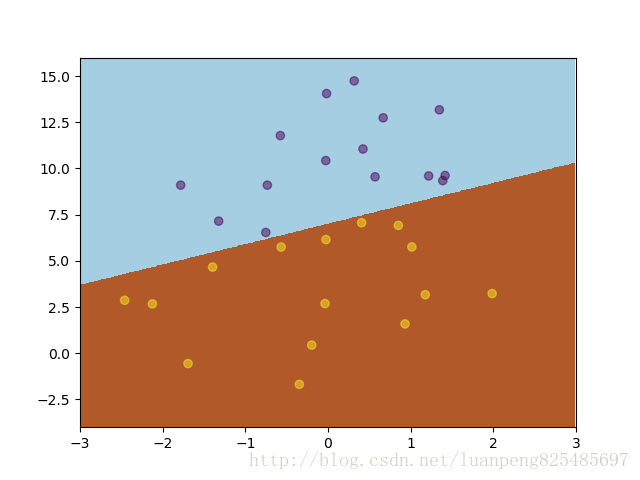
wk+1=wk−ρkxTk(sigmoid(xkwk)−yk)
其中xk为一个样本对象(行向量),yk为该对象的输出(行向量)。
获取回归系数矩阵,绘制分割区域
回归系数矩阵为:
[[-23.98429667 27.70302552]
[ -3.8623706 4.56685091]
[ 3.36581925 -3.90760748]]
绘制出的分割区域为
输出分类和概率为
[[0]] [[ 1.00000000e+00 4.43767950e-13]]
表示输入对象[0.317029,14.739025],属于分类0,因为属于分类0 的概率为1.0,属于分类1的概率为4.43767950e-13。
样本数据集第一列为属性x1,第二列为属性x2,第三列为分类(三种类别)
先将数据集转化为逻辑分类可以处理的数据结构。即,为对象添加值为1的属性x0,将输出分类转换为one-hot编码。
分类0表示为[1,0,0],分类1表示为[0,1,0],分类2表示为[0,0,1]
下面我们先来看看数据是什么样的。
wk+1=wk−ρ∇J(wk)=wk−ρXT(softmax(Xwk)−y)
按照这个公式实现代码
绘制分类区域
权重矩阵w为
[[ -0.76478209 12.94845658 -9.18367448]
[-10.22934766 -1.38818119 14.61752885]
[ 5.38500348 5.07899946 -7.46400295]]
绘制的分割区域为
wk+1=wk−ρkxTk(softmax(xkwk)−yk)
按照这个公式实现代码
绘制分割区域
得到的权重矩阵w为
[[ -0.86015701 4.56667081 -4.7265138 ]
[ -0.4547426 3.74717339 10.49808187]
[ 3.26510843 1.9243891 -3.50245892]]
分割区域为
输出分类和概率为
[[2]] [[ 8.81398647e-08 5.11371774e-02 9.48862734e-01]]
表示输入对象[1.90474358,0.11881899],属于分类2,因为属于分类0 的概率为8.81398647e-08,属于分类1的概率为5.11371774e-02,属于分类2的概率为 9.48862734e-01。
我们知道[1,0]表示的是样本对象100%的概率为分类0,0%的概率为分类1
[0,1]表示的是样本对象0%的概率为分类0,100%的概率为分类1
那我们现在来尝试一下其他的概率表达方式
比如二分类中,分类0是我想要的,分类1不是我想要的。
分类0的值表达成[100%],表示100%是我想要的,
分类1的值表达成[0%],表示0%是我想要的。
我们按照逻辑回归计算出来的概率值就是y只有一个值。这个值表达的是,是我想要的分类的概率,也就是该对象是分类0的概率。这个概率超过50%,我们就可以把他划分为分类0,低于50%,我们就可以划分为分类1。
由于我们使用这种方式进行编码,只计算一个输出值,
所以要计算的回归系数矩阵,就变成了
w0w1w2
而不再是
w00w10w20w01w11w21
实现代码为
运行函数得到的回归系数为
[[-23.98429667]
[ -3.8623706 ]
[ 3.36581925]]
这个回归系数矩阵表达式是y=sigmoid(xw)中的w。
我们通过y>0.5进行分类判别。由于sigmoid是调单递增的。所以判别也就等价于xw>0。将这个公式展开。
1∗w0+x1∗w1+x2∗w2>0
将训练迭代的系数带入公式,
1∗−23.98429667+x1∗−3.8623706+x2∗3.36581925>0
下图绘制出了这条边界线。
python数据挖掘系列教程
线性函数、线性回归
参考:http://blog.csdn.net/luanpeng825485697/article/details/78933084逻辑分类LC
线性模型:把每个特征对分类结果的“作用”加起来——这就是线性模型。逻辑分类(Logistic Classification)是一种线性模型,可以表示为y=f(w∗x+b),其中w是训练得到的权重参数(Weight);x是样本特征数据;b是偏置(Bias),f成为激活函数。
就是给定一批样本数据集,和样本对象所属的分类,进行建立模型。使用模型对新来的对象对象分类预测。
值得注意的是,逻辑分类中,我们想要的结果为分类类型,而不再是线性回归中的数值。
注意:在逻辑分类中,我们想要的结果是对象所属的分类,比如A类、B类,属于标称型数据。但是在数学中,一般没办法使用A、B表示,而使用0、1、2、3表示每种类别。注意这里的0、1、2、3只是表示对应的标称分类,并不表示具体的数值。也就是说,并不能表述为1比0大,就像不能表述为B类比A类大。也不能表述为1比3更靠近0,就像不能表述为B类比C类更靠近A类。必能在逻辑分类的学习中,一定要注意把握这一点。
既然逻辑分类中,我们想要的输出结果不再是数值型的,但是在线性回归中我们学习的都是计算数值型的结果,那怎么应用呢?
我们可以使用一种成为one-hot编码的方式,将分类编码成数值。
比如有4个分类0、1、2、3。我们可以将
分类0编码成[1,0,0,0] 第一个分量的值为1,其他为0,表示为对象属于第一个分类的概率为1,属于其他分类的概率为0。
分类1编码成[0,1,0,0] 第二个分量的值为1,其他为0,表示为对象属于第二个分类的概率为1,属于其他分类的概率为0。
分类2编码成[0,0,1,0] 第三个分量的值为1,其他为0,表示为对象属于第三个分类的概率为1,属于其他分类的概率为0。
分类3编码成[0,0,0,1] 第四个分量的值为1,其他为0,表示为对象属于第四个分类的概率为1,属于其他分类的概率为0。
而分类概率是数值型的,也就是说我们预测的结果就变成了四维数值型的。
重点来了
所以在建立逻辑分类模型前必须先将标称分类,转化为数值型的one-hot编码才能运用线性模型进行数值运算。也就是说逻辑分类一定是多输出的。只不过你在拿到样本数据集时样本数据的结果都是标称型的分类,这种数据集是不能应用于逻辑分类建模的。比如下面是你拿到的数据集。第一列为属性x1,第二列为属性x2,第三列为分类结果,包含0,1,2三种分类
x1 x2 y 0.1 0.2 0 0.12 0.32 0 0.21 0.31 1 0.25 0.15 2
必须先将数据集转化为下面的模式。x0为常值0,对象的回归系数表示偏量值b,标称型分为转化为数值型概率。
x0 x1 x2 y1 y2 y3 1 0.1 0.2 1 0 0 1 0.12 0.32 1 0 0 1 0.21 0.31 0 1 0 1 0.25 0.15 0 0 1
这样我们要求的回归系数矩阵w也不再是线性回归中的向量,而是矩阵。
比如
有m行x,每一个x有n个属性,然后每个x有一个分类,也就有m行y,每个y可以被分成k个元素的向量,我需要先把m行y变成一个m行k列的矩阵,最后计算出一个(j+1)*k列的w矩阵。
线性回归、线性分类、逻辑回归、逻辑分类的区别
线性回归:线性回归就是计算回归系数,通过回归系数线性组合属性预测数值结果。
线性回归以误差平方和最小为目的,其实是在假定误差服从高斯分布
f(x)=wx+b
二分类的线性分类:
在线性回归的基础上添加了大于和小于0的判断。当值大于0属于一种分类,当值小于0等于另一种分类。
f(n)={1,−1,f(x) ≥ 0f(x)<0
逻辑回归:
逻辑回归是逻辑分类的一种。
逻辑分类为
y=f(w∗x+b)
当f函数为sigmoid函数时,就是逻辑回归。即
y=sigmoid(w∗x+b)
逻辑回归就是在线性回归的基础上,再经过sigmoid这个非线性函数,将值转化为分类的概率。 逻辑回归实际上是采用的是 伯努利分布来分析误差。
sigmoid函数:
sigmoid(x)=11+e−x

逻辑分类:
逻辑分类属于线性模型。逻辑分类包含逻辑回归、一般线性回归。逻辑回归为二分类问题,一般线性回归为多分类问题。
二分类:在逻辑回归的基础上,判断分类概率是否大于0.5,大于则属于这个分类。
y={1,−1,f(wx+b) ≥ 0.5f(wx+b)<0.5
而由于sigmoid函数是单调的,当sigmoid的输入为0时,输出为0.5,所以等价于逻辑回归二分类的判别为以下公式,这与线性分类的公式相同。
wx+b=0
多分类:一般线性回归:
高斯分布、伯努利分布、贝塔分布、迪特里特分布,都属于指数分布。所以一般线性回归就是用指数分布来处理噪声模型的方法。一般使用softmax函数来处理多分类问题。softmax回归是一般线性回归的一个例子。
f(wx+b)=softmax(wx+b)
softmax函数
softmax函数其实就是一个归一化的指数函数
softmax(x)=exi∑iexi
在使用一般线性回归进行分类中,计算哪个分类的概率大就属于哪个分类。
逻辑分类的损失函数
我们知道在线性回归中使用误差平方和作为损失函数,求解使损失函数最小的w是线性回归的目的。在逻辑分类中,类别给ont-hot编码为概率。在统计学上,衡量两个概率的分布向量的差异程度,叫做交叉熵(Cross Entropy),
交叉熵函数如下:
D(y,p)=yln(p)+(1−y)(1−ln(p)) 其中p=softmax(wx+b)
逻辑分类中的损失函数为
loss(w,b)=−1/m∑D(yi,pi)
逻辑分类器的构成
在学习逻辑分类之前再强调一遍,必须先将分类进行one-hot编码作为输出结果,后面的学习才能理解。也就是说如果有3种分类,后面的教程每个样本对象的输出结果都是3维的,而不再是线性回归教程中的一维数据结果。线性回归为估值预测而生,逻辑分类为分类预测而生。
下面为线性回归和逻辑分类的模型示例。

逻辑分类是一个包含线性和非线性部分用来进行分类的分类器。我们以n分类为例进行分析。
假设已经知道回归系数矩阵w和偏量b,逻辑分类包含下面的3个步骤。
1、计算线性函数的输出值
根据输入对象x和已知的回归系数矩阵w,以及偏量b,计算输入经过线性函数后的输出值,即h=wx+b。输出值h也是n维的。每一维可以近似认为是待测对象偏向于每种分类的成分。
2、将线性函数的输出结果转化为分类概率
得到了线性函数的输出结果,还需要将每一个维度转化为对象属于每个分类的概率。使得每个概率在0-1之间。这是一步非线性操作,所以这一步不再属于线性回归的范围。
将输出结果转化为概率的函数我们称为阶跃函数,也叫做激活函数。
一般在神经网络中用的最多的是sigmoid和tanh,当然也有用relu的。这是针对“是”和“否”的分类,但当进行多分类时,就要用到softmax 。
如果使用sigmoid函数进行二分类,sigmoid函数的功能在于:
sigmoid(x)=11+e−x
1、将线性函数的输出向量作为输入的“分数”,将“分数”映射在(0,1)之间。
2、以“对数”的方式完成到(0,1)的映射,凸显大的分数的作用,使其输出的概率更高,抑制小分数的输出概率。
如果使用softmax函数进行多分类,softmax函数的功能在于:
softmax(x)=exi∑iexi
1、将线性函数的输出向量作为输入的“分数”,将“分数”映射在(0,1)之间,并且所有分数的和为1。
2、以“对数”的方式完成到(0,1)的映射,凸显其中最大的分数的作用,并抑制远低于最大分数的其他数值。
我们使用代码来看看softmax的效果。
# softmax函数 def softmax(s): return np.exp(s) / np.sum(np.exp(s), axis=0) if __name__ == '__main__': # 查看softmax效果 x = np.arange(-3.0, 6.0, 0.1) # 等差数列 scores = np.vstack([x, np.ones_like(x), 0.2 * np.ones_like(x)]) # vstack将三个矩阵按列堆叠在一起。ones_like全1矩阵。模拟三种线性函数的输出向量作为softmax的输入 plt.plot(x, softmax(scores).T, linewidth=2) # 计算三种softmax函数的输出结果,绘制查看图形,了解softmax的特性:凸显其中最大的分数,抑制远低于最大分数的其他数值 plt.show() # 分数扩大、缩小100倍 scores = np.array([2.0, 1.0, 0.1]) print(softmax(scores)) print(softmax(scores * 100)) print(softmax(scores / 100))

输出:
[ 0.65900114 0.24243297 0.09856589] [ 1.00000000e+00 3.72007598e-44 3.04823495e-83] [ 0.33656104 0.33321221 0.33022675]
根据输出结果我们可以看出,当softmax的输入值被方法100倍时,数值之间的差距被拉大。softmax对这种差距敏感,差距越大,分类器越‘自信’,差距越小,分类器越‘犹豫’。
3、将分类概率转化为类别
这一步就比较简单了,当属于某分类的概率最大时,就可以判定为数据该分类。
那如何求解正确的回归系数w和偏量b呢,因为只有有了正确的w和b,才能带入逻辑分类公式进行分类判别。
(后面的教程就省略b偏量,因为b偏量可以认为是样本一个值为1 的属性对应的权重)
求解回归系数
在逻辑分类器的结构中,我们知道逻辑分类包含了线性函数和激活函数两个过程。线性函数g部分我们表示为:
g(X)=XW
逻辑回归的激活函数f部分我们表示为:
f(z)=sigmoid(z)
softmax回归的激活函数f部分表示为:
f(z)=softmax(z)
当然我们也可以直接将输入x表示为最终的输出结果
y=h(x)=f(z)=f(g(x))=f(xw)
在线性回归中,我们学习了线性回归的梯度下降法和随机梯度下降法,在逻辑回归、甚至以后的神经网络、全连接神经网络、卷积神经网络、循环神经网络都是使用梯度下降法(随机梯度下降法)来进行后向传播算法实现回归系数w或网络层系数w的迭代收敛计算。
梯度下降法的步骤(线性回归、逻辑回归、所有的神经网络都是相同的步骤):
1、写出损失函数。
2、损失函数对自变量w求导,得到w的梯度。
3、根据梯度,更细w权重。
梯度下降法
现在我们先来回归一下线性回归中的梯度下降法。梯度下降法求解的是使损失函数(误差平方和)最小的权重矩阵w。
误差平方和为
J(w)=∑mi=1(xiw−yi)2
对w求导的得到梯度
∇J(w)=2XT(Xw−y)
回归系数更新
wk+1=wk−ρ∗∇J(wk)=wk−ρ∗2XT(Xwk−y)
我们来按照这个步骤解决逻辑回归中的梯度下降。
一般定义逻辑回归的损失函数为
J(w)=−1m∑mi=1[yiloghw(xi)+(1−yi)log(1−hw(xi))]
其中
x(i) 每个样本数据点在某一个特征上的值,即样本对象x的某个属性的值
y(i) 每个样本数据的所属类别标签
m 样本数据点的个数
hw(x) 样本数据的概率密度函数,即某个数据属于1类(二分类问题)的概率
J(w) 代价函数,估计样本属于某类的风险程度,越小代表越有可能属于这类这个
这个损失函数是按照求最大似然函数的方法,求得逻辑回归似然函数后再取对数形成的,喜欢公式的朋友们可以移步http://blog.csdn.net/lookqlp/article/details/51161640
不喜欢公司也没必要记住这个公式,只需要记住下面的w梯度和w更新公式就行。
对损失函数求导得到w的梯度为
∇J(w)=∑mi=1xTi∗(f(xiw)−yi)=XT(f(Xw)−y)=XT(sigmoid(Xw)−y)
其中xi表示第i个样本对象(行向量),yi表示第i个输出结果(行向量),f为激活函数,X为m个样本数据集,每行为一个对象,y为m个输出结果。
再强调一遍,在线性回归中我们一般使用的案例都是预测一个数值型数据,在逻辑回归中代表分类的数字并不是数值型的,所以经过one-hot编码后变成了多个数值型的输出结果。
所以在逻辑回归中,梯度下降法的更新公式为
wk+1=wk−ρ∇J(wk)=wk−ρXT(sigmoid(Xwk)−y)
在有些教程中,喜欢用列向量表示一个样本对象x,则一个对象的输出结果y也是列向量。你看到的逻辑回归的梯度写法不相同,不过不用慌张,它只是数据的行列形式不同罢了。
我们来按照这个步骤解决softmax回归中的梯度下降。
喜欢公式的可以移步https://www.cnblogs.com/Determined22/p/6362951.html
我们只对softmax回归的结果给出。
在softmax回归中,梯度下降法的更新公式为
wk+1=wk−ρ∇J(wk)=wk−ρXT(softmax(Xwk)−y)
所以说线性回归、逻辑回归、softmax回归的梯度更新公式都是一样的。
随机梯度下降法
前面的梯度下降法在每次更新回归系数(最优参数)时,都需要遍历整个数据集。如果有数十亿样本和成千上万的特征,那么该方法的计算复杂度就太高了。现在介绍一种算法,一次只用一个样本点去更新回归系数(最优参数),这样就可以有效减少计算量了,这种方法就叫做随机梯度上升算法。在线性回归中回归系数的更新如下,其中xk为第k个样本对象(行向量)。yk为该对象输出的结果,为数值。
wk+1=wk−2∗ρkxTk(xkwk−yk)
在逻辑回归中,每个对象的输出结果(类别)被one-hot编码成向量,随机梯度下降法的更新公式为
wk+1=wk−ρkxTk(sigmoid(xkwk)−yk)
其中xk为一个样本对象(行向量),yk为该对象的输出(行向量)。
在softmax回归中,随机梯度下降法的更新公式为
wk+1=wk−ρkxTk(softmax(xkwk)−yk)
喜欢数学推导的朋友可以自己去百度,这里就不给出了。
二分类逻辑回归案例
构造数据集
每行为一个对象,每列为一个特征属性,第1列为x1,第2列为x2,最后一列为所属分类。data=[ [-0.017612,14.053064,0], [-0.752157,6.538620,0], [-1.322371,7.152853,0], [0.423363,11.054677,0], [0.569411,9.548755,0], [-0.026632,10.427743,0], [0.667394,12.741452,0], [1.347183,13.175500,0], [1.217916,9.597015,0], [-0.733928,9.098687,0], [1.416614,9.619232,0], [1.388610,9.341997,0], [0.317029,14.739025,0], [-0.576525,11.778922,0], [-1.781871,9.097953,0], [-1.395634,4.662541,1], [0.406704,7.067335,1], [-2.460150,6.866805,1], [0.850433,6.920334,1], [1.176813,3.167020,1], [-0.566606,5.749003,1], [0.931635,1.589505,1], [-0.024205,6.151823,1], [-0.036453,2.690988,1], [-0.196949,0.444165,1], [1.014459,5.754399,1], [1.985298,3.230619,1], [-1.693453,-0.557540,1], [-0.346811,-1.678730,1], [-2.124484,2.672471,1] ]
先将数据集转化为逻辑分类可以处理的数据结构。即,为对象添加值为1的属性x0,将输出分类转换为one-hot编码。
#加载数据集,最后一列最为类别标签,前面的为特征属性的值 def loadDataSet(datasrc): dataMat = np.mat(datasrc) y = dataMat[:, dataMat.shape[1] - 1] # 最后一列为结果列 b = np.ones(y.shape) # 添加全1列向量代表b偏量 X = np.column_stack((b, dataMat[:, 0:dataMat.shape[1] - 1])) # 特征属性集和b偏量组成x X = np.mat(X) labeltype = np.unique(y.tolist()) # 获取分类数目 eyes = np.eye(len(labeltype)) # 每一类用单位矩阵中对应的行代替,表示目标概率。如分类0的概率[1,0,0],分类1的概率[0,1,0],分类2的概率[0,0,1] Y = np.zeros((X.shape[0], len(labeltype))) for i in range(X.shape[0]): Y[i, :] = eyes[int(y[i, 0])] # 读取分类,替换成概率向量。这就要求分类为0,1,2,3,4,5这样的整数 # print(Y) return X, y, Y # X为特征数据集,y为分类数据集,Y为概率集
我们先来看看数据是个什么样子
#可视化样本数据集
def plotDataSet():
dataMat,labelMat,labelPMat = loadDataSet(data) #加载数据集
plt.scatter(dataMat[:,1].flatten().A[0],dataMat[:,2].flatten().A[0],c=labelMat.flatten().A[0]) #第一个偏量为b,第2个偏量x1,第3个偏量x2
plt.xlabel('X1'); plt.ylabel('X2') #绘制label
plt.xlim([-3,3])
plt.ylim([-4,16])
plt.show()
我们使用的样本数据,有两个特征属性,x1和x2如果,算上b偏量就是三个回归系数。结果为2分类。
则线性函数的输出结果为[z0,z1]
z0=w00*1 + w01*x1 + w02*x2
z1=w10*1 + w11*x1 + w12*x2
线性函数的结果[z0,z1]再经过Sigmoid激活函数,可得到预测的分类概率[y0,y1]。当然最开始这个预测的分类概率并不准确,所以需要模型训练,不停的根据预测的结果是否准确来调整回归系数。
其中Sigmoid逻辑回归函数实现如下:
# sigmoid函数,逻辑回归函数,将线性回归值转化为概率的激活函数 def sigmoid(x): return 1.0 / (1 + np.exp(-x))
梯度下降法获取回归系数:
在逻辑回归中,梯度下降法的更新公式为wk+1=wk−ρ∇J(wk)=wk−ρXT(sigmoid(Xwk)−y)
按照这个公式实现代码
# 逻辑回归中使用梯度下降法求回归系数。逻辑回归和线性回归中原理相同,只不过逻辑回归使用sigmoid作为迭代进化函数。因为逻辑回归是为了分类而生。线性回归为了预测而生 def gradAscent(dataMat, labelPMat): m, n = np.shape(dataMat) #返回dataMatrix的大小。m为行数,n为列数。 alpha = 0.05 #移动步长,也就是学习速率,控制更新的幅度。 maxCycles = 1000 #最大迭代次数 weights = np.ones((n,labelPMat.shape[1])) #初始化权重列向量 for k in range(maxCycles): h = sigmoid(dataMat * weights) #梯度上升矢量化公式,计算预测值(列向量)。每一个样本产生一个预测值 error = h-labelPMat #计算每一个样本预测值误差 weights = weights - alpha * dataMat.T * error # 根据所有的样本产生的误差调整回归系数 return weights.getA() # 将矩阵转换为数组,返回回归系数数组
绘制分类区域
# 分类只能绘制分界区域。而不是通过分割线来可视化 def plotBestFit(dataMat,labelMat,weights): # 先产生x1和x2取值范围上的网格点,并预测每个网格点上的值。 step = 0.02 x1_min, x1_max = -3,3 x2_min, x2_max = -4,16 xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, step), np.arange(x2_min, x2_max, step)) testMat = np.c_[xx1.ravel(), xx2.ravel()] #形成测试特征数据集 testMat = np.column_stack((np.ones(((testMat.shape[0]),1)),testMat)) #添加第一列为全1代表b偏量 testMat = np.mat(testMat) y = sigmoid(testMat*weights) #输出每个样本属于每个分类的概率 predicted = y.argmax(axis=1) #获取每行最大值的位置,位置索引就是分类 predicted = predicted.reshape(xx1.shape).getA() # 绘制区域网格图 plt.pcolormesh(xx1, xx2, predicted, cmap=plt.cm.Paired) # 再绘制一遍样本数据点,这样方便查看 plt.scatter(dataMat[:, 1].flatten().A[0], dataMat[:, 2].flatten().A[0], c=labelMat.flatten().A[0], alpha=.5) # 第一个偏量为b,第2个偏量x1,第3个偏量x2 plt.xlim([-3,3]) plt.ylim([-4,16]) plt.show() if __name__ == '__main__': dataMat, labelMat, labelPMat = loadDataSet(data) # 加载数据集 weights = gradAscent(dataMat, labelPMat) # 梯度下降法求回归系数 print(weights) plotBestFit(dataMat,labelMat,weights)
回归系数矩阵w为:
[[-25.38603398 25.43723638]
[ -3.98349475 3.99351765]
[ 3.60847635 -3.61579463]]
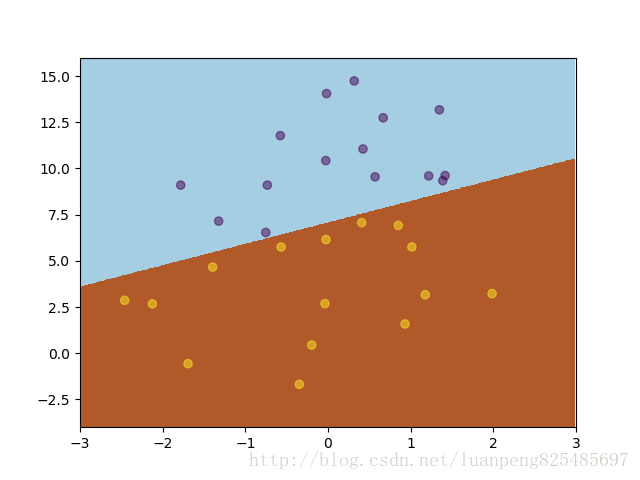
绘制出的分割区域为

随机梯度下降法获取回归系数:
在逻辑回归中,随机梯度下降法的更新公式为wk+1=wk−ρkxTk(sigmoid(xkwk)−yk)
其中xk为一个样本对象(行向量),yk为该对象的输出(行向量)。
# 逻辑回归中使用随机梯度下降算法。numIter为迭代次数。改进之处:alpha移动步长是变化的。一次只用一个样本点去更新回归系数,这样就可以有效减少计算量了 def stocGradAscent(dataMatrix, labelPMat, numIter=500): m,n = np.shape(dataMatrix) #返回dataMatrix的大小。m为样本对象的数目,n为列数。 weights = np.ones((n,labelPMat.shape[1])) #参数初始化 for j in range(numIter): for k in range(m): # 遍历m个样本对象 alpha = 10/(1.0+j+k)+0.01 #降低alpha的大小,每次减小1/(j+i)。刚开始的时候可以步长大一点,后面调整越精细 h = sigmoid(dataMatrix[k]*weights) #选择随机选取的一个样本,计算预测值h error = h-labelPMat[k] #计算一个样本的误差 weights = weights - alpha * dataMatrix[k].T*error #更新回归系数 return weights.getA() #将矩阵转换为数组,返回回归系数数组
获取回归系数矩阵,绘制分割区域
if __name__ == '__main__': dataMat, labelMat, labelPMat = loadDataSet(data) # 加载数据集 weights = stocGradAscent(dataMat, labelPMat) # 局部梯度下降法求回归系数 print(weights) plotBestFit(dataMat,labelMat,weights)
回归系数矩阵为:
[[-23.98429667 27.70302552]
[ -3.8623706 4.56685091]
[ 3.36581925 -3.90760748]]
绘制出的分割区域为

对新对象进行预测
有了回归系数矩阵,就可以对逻辑回归问题进行分类了。# 对新对象进行预测 def predict(weights,testdata): testdata.insert(0, 1.0) #现在首部添加1代表b偏量 testMat = np.mat([testdata]) y=sigmoid(testMat * np.mat(weights)) # 对输入进行预测 type = y.argmax(axis=1) # 概率最大的分类就是预测分类。由于输出值y为行向量,所按行取最大值的位置 return type, y # type为所属分类,h为属于每种分类的概率 if __name__ == '__main__': dataMat, labelMat, labelPMat = loadDataSet(data) # 加载数据集 weights = gradAscent(dataMat, labelPMat) # 梯度下降法求回归系数 # weights = gradAscent(dataMat, labelPMat) # 梯度下降法求回归系数 print(weights) type,h = predict(weights,[0.317029,14.739025]) print(type,h)
输出分类和概率为
[[0]] [[ 1.00000000e+00 4.43767950e-13]]
表示输入对象[0.317029,14.739025],属于分类0,因为属于分类0 的概率为1.0,属于分类1的概率为4.43767950e-13。
多分类softmax回归
加载数据集
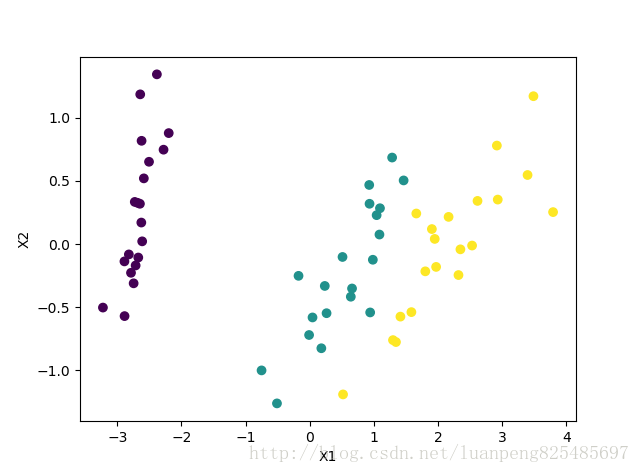
数据集就采用如下的数据,和二分类的区别在于类别有三种:0,1,2。样本数据集第一列为属性x1,第二列为属性x2,第三列为分类(三种类别)
# 样本数据集,第一列为x1,第二列为x2,第三列为分类(三种类别) data=[ [-2.68420713, 0.32660731, 0],[-2.71539062, -0.16955685, 0],[-2.88981954, -0.13734561, 0],[-2.7464372, -0.31112432, 0],[-2.72859298, 0.33392456, 0], [-2.27989736, 0.74778271, 0],[-2.82089068, -0.08210451, 0],[-2.62648199, 0.17040535, 0],[-2.88795857, -0.57079803, 0],[-2.67384469, -0.1066917, 0], [-2.50652679,0.65193501,0],[-2.61314272,0.02152063,0],[-2.78743398,-0.22774019,0],[-3.22520045,-0.50327991,0],[-2.64354322,1.1861949,0], [-2.38386932,1.34475434,0],[-2.6225262,0.81808967,0],[-2.64832273,0.31913667,0],[-2.19907796,0.87924409,0],[-2.58734619,0.52047364,0], [1.28479459, 0.68543919, 1],[0.93241075, 0.31919809, 1],[1.46406132, 0.50418983, 1],[0.18096721, -0.82560394, 1],[1.08713449, 0.07539039, 1], [0.64043675, -0.41732348, 1],[1.09522371, 0.28389121, 1],[-0.75146714, -1.00110751, 1],[1.04329778, 0.22895691, 1],[-0.01019007, -0.72057487, 1], [-0.5110862,-1.26249195,1],[0.51109806,-0.10228411,1],[0.26233576,-0.5478933,1],[0.98404455,-0.12436042,1],[-0.174864,-0.25181557,1], [0.92757294,0.46823621,1],[0.65959279,-0.35197629,1],[0.23454059,-0.33192183,1],[0.94236171,-0.54182226,1],[0.0432464,-0.58148945,1], [2.53172698, -0.01184224, 2],[1.41407223, -0.57492506, 2],[2.61648461, 0.34193529, 2],[1.97081495, -0.18112569, 2],[2.34975798, -0.04188255, 2], [3.39687992, 0.54716805, 2],[0.51938325, -1.19135169, 2],[2.9320051, 0.35237701, 2],[2.31967279, -0.24554817, 2],[2.91813423, 0.78038063, 2], [1.66193495,0.2420384,2],[1.80234045,-0.21615461,2],[2.16537886,0.21528028,2],[1.34459422,-0.77641543,2],[1.5852673,-0.53930705,2], [1.90474358,0.11881899,2],[1.94924878,0.04073026,2],[3.48876538,1.17154454,2],[3.79468686,0.25326557,2],[1.29832982,-0.76101394,2], ]
先将数据集转化为逻辑分类可以处理的数据结构。即,为对象添加值为1的属性x0,将输出分类转换为one-hot编码。
分类0表示为[1,0,0],分类1表示为[0,1,0],分类2表示为[0,0,1]
# 加载数据集,最后一列最为类别标签,前面的为特征属性的值 def loadDataSet(dataarr): # 生成X和y矩阵 dataMat = np.mat(dataarr) y = dataMat[:, dataMat.shape[1] - 1] # 最后一列为结果列 b = np.ones(y.shape) # 添加全1列向量代表b偏量 X = np.column_stack((b, dataMat[:, 0:dataMat.shape[1] - 1])) # 特征属性集和b偏量组成x X = np.mat(X) labeltype = np.unique(y.tolist()) # 获取分类数目 eyes = np.eye(len(labeltype)) # 每一类用单位矩阵中对应的行代替,表示目标概率。如分类0的概率[1,0,0],分类1的概率[0,1,0],分类2的概率[0,0,1] Y=np.zeros((X.shape[0],len(labeltype))) for i in range(X.shape[0]): Y[i,:] = eyes[int(y[i,0])] # 读取分类,替换成概率向量。这就要求分类为0,1,2,3,4,5这样的整数 return X, y,Y #X为特征数据集,y为分类数据集,Y为概率集
下面我们先来看看数据是什么样的。
#可视化样本数据集
def plotDataSet():
dataMat,labelMat,labelPMat = loadDataSet() #加载数据集
plt.scatter(dataMat[:,1].flatten().A[0],dataMat[:,2].flatten().A[0],c=labelMat.flatten().A[0]) #第一个偏量为b,第2个偏量x1,第3个偏量x2
plt.xlabel('X1'); plt.ylabel('X2') #绘制label
plt.show()
softmax回归的梯度下降法
在softmax回归中,梯度下降法的更新公式为wk+1=wk−ρ∇J(wk)=wk−ρXT(softmax(Xwk)−y)
按照这个公式实现代码
# softmax函数,将线性回归值转化为概率的激活函数。输入s要是行向量 def softmax(s): return np.exp(s) / np.sum(np.exp(s), axis=1) # 逻辑回归中使用梯度下降法求回归系数。逻辑回归和线性回归中原理相同,只不过逻辑回归使用sigmoid作为迭代进化函数。因为逻辑回归是为了分类而生。线性回归为了预测而生 def gradAscent(dataMat, labelPMat): alpha = 0.2 #移动步长,也就是学习速率,控制更新的幅度。 maxCycles = 1000 #最大迭代次数 weights = np.ones((dataMat.shape[1],labelPMat.shape[1])) #初始化权回归系数矩阵 系数矩阵的行数为特征矩阵的列数,系数矩阵的列数为分类数目 for k in range(maxCycles): h = softmax(dataMat*weights) #梯度上升矢量化公式,计算预测值(行向量)。每一个样本产生一个概率行向量 error = h-labelPMat #计算每一个样本预测值误差 weights = weights - alpha * dataMat.T * error # 根据所有的样本产生的误差调整回归系数 return weights # 将矩阵转换为数组,返回回归系数数组
绘制分类区域
# 多分类只能绘制分界区域。而不是通过分割线来可视化 def plotBestFit(dataMat,labelMat,weights): # 获取数据边界值,也就属性的取值范围。 x1_min, x1_max = dataMat[:, 1].min() - .5, dataMat[:, 1].max() + .5 x2_min, x2_max = dataMat[:, 2].min() - .5, dataMat[:, 2].max() + .5 # 产生x1和x2取值范围上的网格点,并预测每个网格点上的值。 step = 0.02 xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, step), np.arange(x2_min, x2_max, step)) testMat = np.c_[xx1.ravel(), xx2.ravel()] #形成测试特征数据集 testMat = np.column_stack((np.ones(((testMat.shape[0]),1)),testMat)) #添加第一列为全1代表b偏量 testMat = np.mat(testMat) # 预测网格点上的值 y = softmax(testMat*weights) #输出每个样本属于每个分类的概率 # 判断所属的分类 predicted = y.argmax(axis=1) #获取每行最大值的位置,位置索引就是分类 predicted = predicted.reshape(xx1.shape).getA() # 绘制区域网格图 plt.pcolormesh(xx1, xx2, predicted, cmap=plt.cm.Paired) # 再绘制一遍样本点,方便对比查看 plt.scatter(dataMat[:, 1].flatten().A[0], dataMat[:, 2].flatten().A[0], c=labelMat.flatten().A[0],alpha=.5) # 第一个偏量为b,第2个偏量x1,第3个偏量x2 plt.show() if __name__ == '__main__': dataMat, labelMat,labelPMat = loadDataSet(data) # 加载数据集 # 梯度下降法 weights = gradAscent(dataMat, labelPMat) # 梯度下降法求回归系数 print(weights) plotBestFit(dataMat,labelMat,weights)
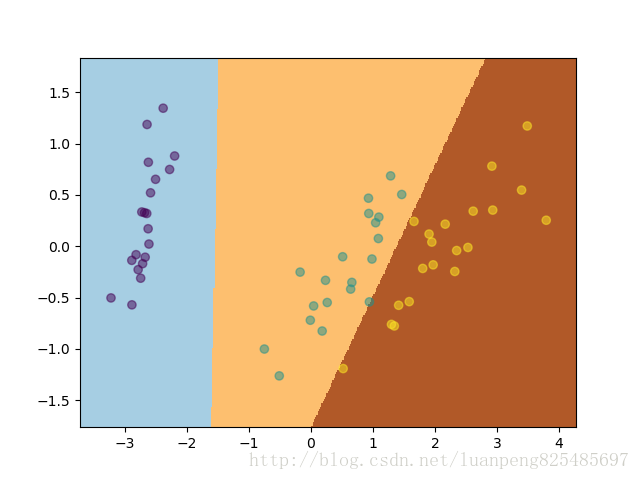
权重矩阵w为
[[ -0.76478209 12.94845658 -9.18367448]
[-10.22934766 -1.38818119 14.61752885]
[ 5.38500348 5.07899946 -7.46400295]]
绘制的分割区域为

softmax回归的随机梯度下降法
在softmax回归中,随机梯度下降法的更新公式为wk+1=wk−ρkxTk(softmax(xkwk)−yk)
按照这个公式实现代码
# 逻辑回归中使用随机梯度下降算法。numIter为迭代次数。改进之处:alpha移动步长是变化的。一次只用一个样本点去更新回归系数,这样就可以有效减少计算量了 def stocGradAscent(dataMatrix, labelPMat, numIter=500): m,n = np.shape(dataMatrix) #返回dataMatrix的大小。m为样本对象的数目,n为列数。 weights = np.ones((n,labelPMat.shape[1])) #参数初始化 for j in range(numIter): for k in range(m): # 遍历m个样本对象 alpha = 2/(1.0+j+k)+0.01 #降低alpha的大小,每次减小1/(j+i)。刚开始的时候可以步长大一点,后面调整越精细 h = softmax(dataMatrix[k]*weights) #选择随机选取的一个样本,计算预测值h error = h-labelPMat[k] #计算一个样本的误差 weights = weights - alpha * dataMatrix[k].T*error #更新回归系数 return weights.getA() #将矩阵转换为数组,返回回归系数数组
绘制分割区域
if __name__ == '__main__': dataMat, labelMat,labelPMat = loadDataSet(data) # 加载数据集 # 梯度下降法 weights = stocGradAscent(dataMat, labelPMat) # 梯度下降法求回归系数 print(weights) plotBestFit(dataMat,labelMat,weights)
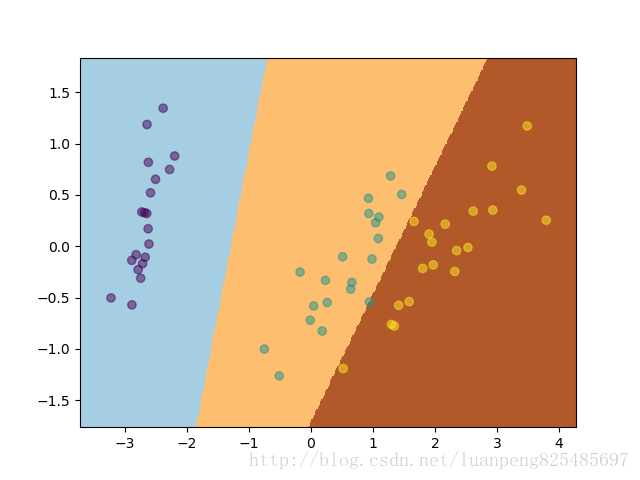
得到的权重矩阵w为
[[ -0.86015701 4.56667081 -4.7265138 ]
[ -0.4547426 3.74717339 10.49808187]
[ 3.26510843 1.9243891 -3.50245892]]
分割区域为

对新对象进行预测
有了回归系数矩阵,就可以对softmax回归问题进行多分类了。# 对新对象进行预测 def predict(weights,testdata): testdata.insert(0, 1.0) #现在首部添加1代表b偏量 testMat = np.mat([testdata]) y=softmax(testMat * np.mat(weights)) type = y.argmax(axis=1) # 概率最大的分类就是预测分类。由于输出值y为行向量,所按行取最大值的位置 return type,y #type为所属分类,h为属于每种分类的概率 if __name__ == '__main__': dataMat, labelMat, labelPMat = loadDataSet(data) # 加载数据集 weights = gradAscent(dataMat, labelPMat) # 梯度下降法求回归系数 # weights = gradAscent(dataMat, labelPMat) # 梯度下降法求回归系数 print(weights) type,h = predict(weights,[1.90474358,0.11881899]) print(type,h)
输出分类和概率为
[[2]] [[ 8.81398647e-08 5.11371774e-02 9.48862734e-01]]
表示输入对象[1.90474358,0.11881899],属于分类2,因为属于分类0 的概率为8.81398647e-08,属于分类1的概率为5.11371774e-02,属于分类2的概率为 9.48862734e-01。
其他方式的编码
在逻辑回归中,二分类0和1一般要按one-hot编码成[1,0]和[0,1]。我们知道[1,0]表示的是样本对象100%的概率为分类0,0%的概率为分类1
[0,1]表示的是样本对象0%的概率为分类0,100%的概率为分类1
那我们现在来尝试一下其他的概率表达方式
比如二分类中,分类0是我想要的,分类1不是我想要的。
分类0的值表达成[100%],表示100%是我想要的,
分类1的值表达成[0%],表示0%是我想要的。
我们按照逻辑回归计算出来的概率值就是y只有一个值。这个值表达的是,是我想要的分类的概率,也就是该对象是分类0的概率。这个概率超过50%,我们就可以把他划分为分类0,低于50%,我们就可以划分为分类1。
由于我们使用这种方式进行编码,只计算一个输出值,
所以要计算的回归系数矩阵,就变成了
w0w1w2
而不再是
w00w10w20w01w11w21
实现代码为
import matplotlib.pyplot as plt
import numpy as np
import random
# 样本数据集,第一列为x1,第二列为x2,第三列为分类(二种类别),必须用0和1表示分类
data=[
[-0.017612, 14.053064, 0],[-0.752157, 6.538620, 0],[-1.322371, 7.152853, 0],[0.423363, 11.054677, 0],[0.569411, 9.548755, 0],
[-0.026632, 10.427743, 0],[0.667394, 12.741452, 0],[1.347183, 13.175500, 0],[1.217916, 9.597015, 0],[-0.733928, 9.098687, 0],
[1.416614, 9.619232, 0],[1.388610, 9.341997, 0],[0.317029, 14.739025, 0],[-0.576525, 11.778922, 0],[-1.781871, 9.097953, 0],
[-1.395634, 4.662541, 1],[0.406704, 7.067335, 1],[-2.460150, 2.866805, 1],[0.850433, 6.920334, 1],[1.176813, 3.167020, 1],
[-0.566606, 5.749003, 1],[0.931635, 1.589505, 1],[-0.024205, 6.151823, 1],[-0.036453, 2.690988, 1],[-0.196949, 0.444165, 1],
[1.014459, 5.754399, 1],[1.985298, 3.230619, 1],[-1.693453, -0.557540, 1],[-0.346811, -1.678730, 1],[-2.124484, 2.672471, 1]
]
#加载数据集,最后一列最为类别标签,前面的为特征属性的值
def loadDataSet(datasrc):
dataMat = np.mat(datasrc)
y = dataMat[:, dataMat.shape[1] - 1] # 最后一列为结果列
b = np.ones(y.shape) # 添加全1列向量代表b偏量
X = np.column_stack((b, dataMat[:, 0:dataMat.shape[1] - 1])) # 特征属性集和b偏量组成x
X = np.mat(X)
for i in range(y.shape[0]):
if y[i]==1:y[i]=0.0 # 分类1不是我想要的分类,所以概率写成0.0
elif y[i] == 0: y[i] = 1.0 # 分类0是我想要的分类,所以概率写成1.0
y=np.mat(y)
return X, y # X为特征数据集,y为分类数据集,Y为概率集
#可视化样本数据集 def plotDataSet(): dataMat,labelMat,labelPMat = loadDataSet(data) #加载数据集 plt.scatter(dataMat[:,1].flatten().A[0],dataMat[:,2].flatten().A[0],c=labelMat.flatten().A[0]) #第一个偏量为b,第2个偏量x1,第3个偏量x2 plt.xlabel('X1'); plt.ylabel('X2') #绘制label plt.xlim([-3,3]) plt.ylim([-4,16]) plt.show()
# sigmoid函数,逻辑回归函数,将线性回归值转化为概率的激活函数 def sigmoid(x): return 1.0 / (1 + np.exp(-x))
# 逻辑回归中使用梯度下降法求回归系数。逻辑回归和线性回归中原理相同,只不过逻辑回归使用sigmoid作为迭代进化函数。因为逻辑回归是为了分类而生。线性回归为了预测而生
def gradAscent(dataMat, labelPMat):
m, n = np.shape(dataMat) #返回dataMatrix的大小。m为行数,n为列数。
alpha = 0.05 #移动步长,也就是学习速率,控制更新的幅度。
maxCycles = 1000 #最大迭代次数
weights = np.ones((n,1)) #初始化权重列向量
for k in range(maxCycles):
h = sigmoid(dataMat * weights) #梯度上升矢量化公式,计算预测值(列向量)。每一个样本产生一个预测值
error = h-labelPMat #计算每一个样本预测值误差
weights = weights - alpha * dataMat.T * error # 根据所有的样本产生的误差调整回归系数
return weights.getA() # 将矩阵转换为数组,返回回归系数数组
# 逻辑回归中使用随机梯度下降算法。numIter为迭代次数。改进之处:alpha移动步长是变化的。一次只用一个样本点去更新回归系数,这样就可以有效减少计算量了
def stocGradAscent(dataMatrix, labelMat, numIter=500):
m,n = np.shape(dataMatrix) #返回dataMatrix的大小。m为样本对象的数目,n为列数。
weights = np.ones((n,1)) #参数初始化
for j in range(numIter):
for k in range(m): # 遍历m个样本对象
alpha = 10/(1.0+j+k)+0.01 #降低alpha的大小,每次减小1/(j+i)。刚开始的时候可以步长大一点,后面调整越精细
h = sigmoid(dataMatrix[k]*weights) #选择随机选取的一个样本,计算预测值h
error = h-labelMat[k] #计算一个样本的误差
weights = weights - alpha * dataMatrix[k].T*error #更新回归系数
return weights.getA() #将矩阵转换为数组,返回回归系数数组
# 对新对象进行预测
def predict1(weights,testdata):
testdata.insert(0, 1.0) #现在首部添加1代表b偏量
testMat = np.mat([testdata])
z = testMat * np.mat(weights)
y=sigmoid(z)
if y>0.5:
# if z>0: #h>0.5的判断等价于 z>0
return 1,y
else:
return 0,y
# 绘制分界线。
def plotBestFit(dataMat,labelMat,weights):
plt.scatter(dataMat[:, 1].flatten().A[0], dataMat[:, 2].flatten().A[0],
c=labelMat.flatten().A[0],alpha=.5) # 第一个偏量为b,第2个偏量x1,第3个偏量x2
x1 = np.arange(-4.0, 4.0, 0.1)
x2 = (-weights[0] - weights[1] * x1) / weights[2] # 逻辑回归获取的回归系数,满足w0+w1*x1+w2*x2=0,即x2 =(-w0-w1*x1)/w2
plt.plot(x1, x2)
plt.xlabel('X1'); plt.ylabel('X2') #绘制label
plt.show()
if __name__ == '__main__':
# 查看数据集的分布
# plotDataSet()
dataMat, labelMat = loadDataSet(data) # 加载数据集
weights = gradAscent(dataMat, labelMat) # 梯度下降法求回归系数
# weights = stocGradAscent(dataMat, labelMat) # 局部梯度下降法求回归系数
print(weights)
type,y = predict1(weights,[0.317029,14.739025])
print(type,y)
plotBestFit(dataMat,labelMat,weights)
运行函数得到的回归系数为
[[-23.98429667]
[ -3.8623706 ]
[ 3.36581925]]
这个回归系数矩阵表达式是y=sigmoid(xw)中的w。
我们通过y>0.5进行分类判别。由于sigmoid是调单递增的。所以判别也就等价于xw>0。将这个公式展开。
1∗w0+x1∗w1+x2∗w2>0
将训练迭代的系数带入公式,
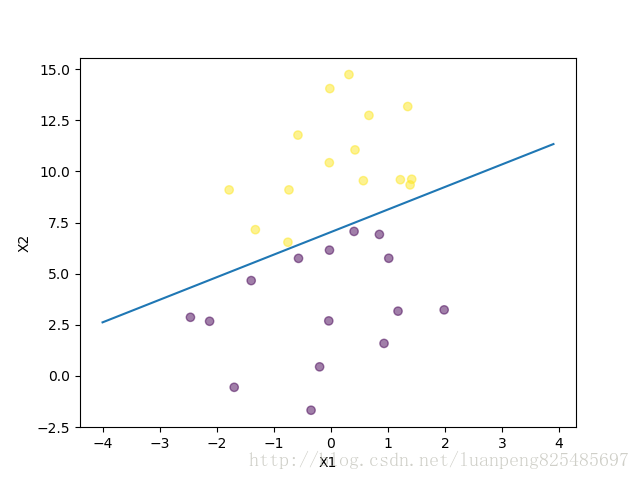
1∗−23.98429667+x1∗−3.8623706+x2∗3.36581925>0
下图绘制出了这条边界线。

相关文章推荐
- python机器学习案例系列教程——线性函数、线性回归
- python机器学习案例系列教程——GBDT算法
- 分类算法系列2----逻辑回归Logistic原理和Python实现
- python机器学习案例系列教程——优化,寻找使成本函数最小的最优解
- 用Python开始机器学习(7:逻辑回归分类)
- python机器学习案例系列教程——K最近邻算法(KNN)、kd树
- python机器学习案例系列教程——模型评估
- python机器学习案例系列教程——极大似然估计、EM算法
- 机器学习(二)广义线性模型:逻辑回归与Softmax分类
- python机器学习案例系列教程——决策树(ID3、C4.5、CART)
- python机器学习案例系列教程——集成学习(Bagging、Boosting、随机森林RF、AdaBoost、GBDT、xgboost)
- python机器学习案例系列教程——文档分类器,朴素贝叶斯分类器,费舍尔分类器
- python机器学习案例系列教程——支持向量机SVM、核函数
- 用Python开始机器学习(7:逻辑回归分类) --好!!
- 机器学习总结(二):线性回归、逻辑斯谛回归(LR)、softmax回归、过拟合
- 【机器学习系列之二】逻辑回归(LR,Logistic Regression)
- python机器学习案例系列教程——DBSCAN密度聚类
- python机器学习案例系列教程——关联分析(Apriori、FP-growth)
- 用Python开始机器学习(7:逻辑回归分类)
- python机器学习案例系列教程——BIRCH聚类
