二分搜索树的删除节点操作
2017-12-23 21:50
369 查看
本节我们来讨论一下对二叉搜索树的删除节点操作。
首先,我们先来研究一下稍微简单一点的问题,如何删除二叉树中的最小值和最大值。
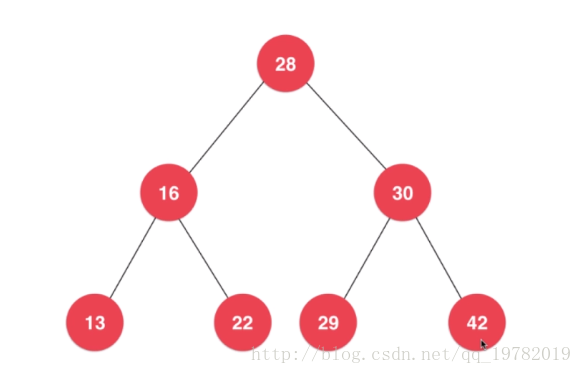
例如上图的这一棵二叉树中,最小值节点和最大值节点都在哪里呢?我们可以很清楚的从图中看出,13是该树的最小节点,42是该树的最大节点,且13节点位于树的最左边,而42位于树的最右边,这难道是一种巧合吗?当然不是,首先,让我们来回忆一下二叉树的一个非常重要的性质。
二叉树根节点的左子树都比根节点小,右子树都比根节点大。
也就是说,对于根节点28来说,他的左子树都比28小,右子树都比28大。那么我们就看28的左子树中的根16,而16又是一颗二叉树的根节点,根据二叉树根节点的左子树都比根节点小,右子树都比根节点大的原则,13比16小,22比16大,因此到13节点了,但是13节点左子树为空,也就是说没有节点比13还要小了,那么13就是这颗二叉树中的最小的节点了,同理,二叉树的最大的节点也可以很容易的得出了。
先从简单的问题开始,让我们来先讨论一下如何找到一颗二叉树的最小节点吧。
通过上面的讨论,我们已经了解到了一棵二叉树的最小值节点位于这颗树的“最左边”,最大节点位于这棵树的“最右边”,因此我们可以很容易的写出一个查找二叉树中最小节点的方法,代码如下所示:
二叉树根节点的左子树都比根节点小,右子树都比根节点大。
二叉树根节点的左子树都比根节点小,右子树都比根节点大。
二叉树根节点的左子树都比根节点小,右子树都比根节点大。
重要的事情说三遍!!上面这句话概括了这个算法的核心思想。
对于查找一棵树的最大节点,同理代码如下:
现在我们知道了如何查找到一颗树中的最小节点和最大节点了,那么要删除这个节点该怎么做呢?
这个时候,我们就要分情况一个一个讨论了。
例如我们拿下面的这棵二叉树来讨论:
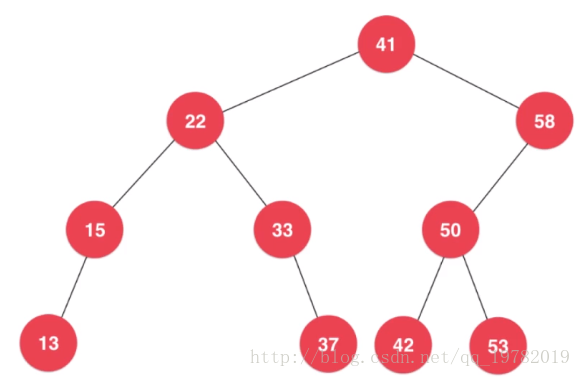
首先,我们可以很清楚的找到这棵二叉树的最小节点是13节点,我们要删除它直接delete掉这个节点就好了,接下来,15是最小节点,我们也delete掉,然而,对于接下来的最小节点22来说,这个节点貌似就不是这么简单的就能够删除了。
如果我们直接把22节点给delete掉,我们来看一下会发生什么样的问题。
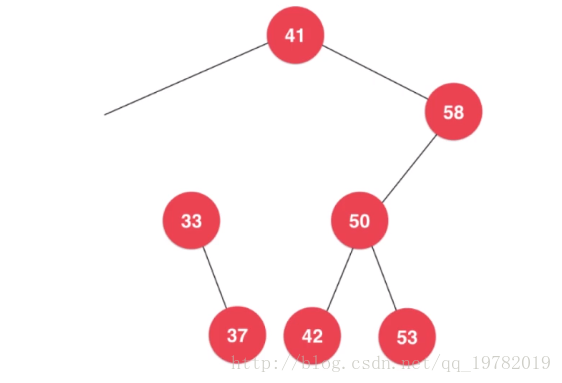
虽然22节点成功删除了,但是,22的右子树却也因为22节点的删除而与原来的二叉树给“断开了”,那么这是失败的一次删除,因为我们在删除22节点的同时,还破坏了这棵树的完整性。那么,我们有什么好的办法呢?
办法当然是有的,首先,虽然22节点被删除了,但是22节点虽然没有左子树了,但是它的右子树我们不能“丢弃”人家,我们要让它重新与原来的树给连接起来,那么对于这段“被丢弃”的右子树的树根来说,我们想一想它具有什么特点呢?33节点能完美的替代被删除的22节点的位置吗?能不能替代,在二叉树中就是判断这两个节点在树中的“状态”是不是一样的。对于被删除的22节点来说,22节点比它的根节点41小,且小于它的左子树,大于它的右子树。而对于“被丢弃”的右子树的树根节点33来说,因为它也处于树根节点41的的子树中,也就是它比根节点41小,而且本来满足它比它的左子树小,右子树大的特点,因此我们发现,33节点与被删除的22节点此时代表的是完全的一样的,因此我们只要把33节点的地址返回给上一层节点(41节点),作为其新的左孩子,这样,我们不仅把22节点成功删除了,而且也使得22节点的右子树没有被“抛弃”,并且重新和原来的树组合起来,完美的符合了二叉树的结构特点。那么就让我们来看一下具体的代码吧。
其中的参数rootnode第一次代表的是需要本删除最小节点的树根地址,后面每次递归中的rootnode都为本层节点的地址。
同理,删除树中最大节点的代码如下:
好了,现在我们已经能够很轻松实现删除一棵以root为根的二叉树的最小值和最大值,并且把新树的根地址返回的方法了。那么,让我们现在来继续往更深入的探讨一下,如何删除二叉树中的任意一个节点呢?
让我们想一想,在二叉树中的每一棵节点,存在哪几种状态呢?
1.无左子树,无右子树。
2.无左子树,有右子树。
3.有左子树,无右子树。
4.既有左子树,也有右子树。
因此,我们在删除树中的一个节点来说,也要去分情况讨论了。
1.无左子树,无右子树。
这种情况很简单,我们只要删除该节点,并且返回一个NULL值给上一层节点做连接使用(可能是被连接到上一层节点的左子树也可能是右子树),但是都不影响二叉树的结构。
1.无左子树,有右子树。
此时这种情况就和我们删除一棵树中的最小节点的处理方法类似了。我们只需要先把被删除节点的右子树信息(右子树根地址)给保存下来以备上一层连接使用,然后在去删除该节点(顺序不能反,否则先把节点删除了,则也丢失了该节点右子树的信息,右子树也一起消失了)。
3.有左子树,无右子树
此时这种情况就和我们删除一棵树中的最大节点的处理方法类似了。我们只需要先
把被删除节点的左子树信息(左子树根地址)给保存下来以备上一层连接使用,然后在
去删除该节点(顺序不能反,否则先把节点删除了,则也丢失了该节点左子树的信息,
左子树也一起消失了)。
4.既有左子树,也有右子树。
这种情况是最复杂的,处理起来也是最难的。:
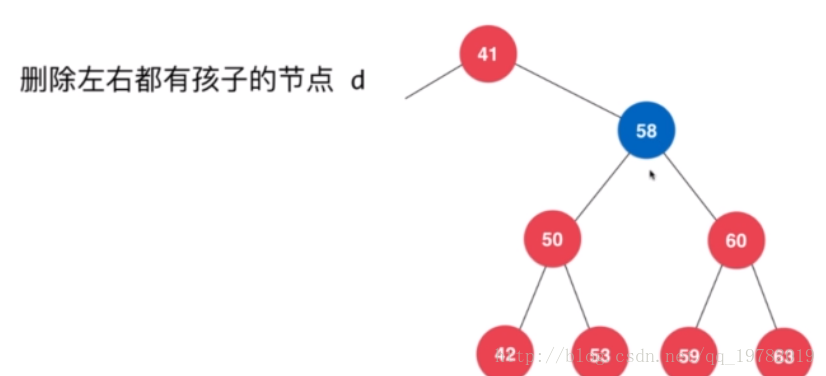
假设我们要删除58这个节点,但是58既有左子树,也有右子树,那么我们应该选择哪一
个节点作为“替代节点呢”?上面我们讨论了删除只含有单边子树情况是如何挑选替代节点
就是其左子树或右子树的树根作为替代节点(也就是该节点的左孩子或者右孩子)。然而,
此时我们这个节点既含有左子树也还有右子树,那么该选哪个孩子作为节点呢?是50节点
还是56节点呢?答案是哪个孩子节点都不选。因为他们都不符合58节点所处的“状态”。
那么58节点此时的状态是怎怎样的呢?还是回到我们对于二叉树结构的定义上:二叉
树根节点的左子树都比根节点小,右子树都比根节点大。
我们发现,58节点比它左子树所有的节点都要小,比它右子树所有节点都要大。那么,假设我们让左孩子50替代58的位置,我们来看一看,50确实是比58的右子树所有的节点都要小,但是50却并不比58左子树的所有节点都要大,比如其中的53节点就要比50大,因此50节点肯定是不符合二叉树结构的特点的,也就不能去代替58节点的位置了。那么我们再来看一下58的右孩子60能否替代58节点的位置呢?如果60替代58节点的位置,原来58节点的左子树的所有节点确实比60要小,满足左子树的关系,但是58的右子树的所有节点却并不是都比60大,比如其中的59节点。因此58的右孩子60节点也不能够完美的胜任这个任务。
那我我们应该选择哪一个节点作为替代节点呢?我们发现,作为替代节点必须满足的条件是:
二叉树根节点的左子树都比根节点小,右子树都比根节点大。
因此,我们需要找58节点的替代节点,因为58节点的左子树所有节点都比58小,所以如
果我们在58左子树中找到一个最大的节点作为替代节点。则这个节点我们发现比58左子
树的所有节点都要大,而且一定是比58节点的右子树所有节点都要小的(因为该节点位
于58节点的左子树,所以肯定比58节点的右子树所有节点都要小,二叉树的结构定义)。
此时,肯定有些聪明的同学会想到了,我们在58右子树中找到一个最小节点作为替
代节点。这样寻找替代节点也是可行的,一样是符合二叉树的结构定义的。右子树的最
小节点本身就比右子树所有节点要小,然后根据二叉树的结构特点也能够很轻松的得出
要比左子树所有的节点都要大的。接下来我们以右子树的最小节点作为替代节点来讨论
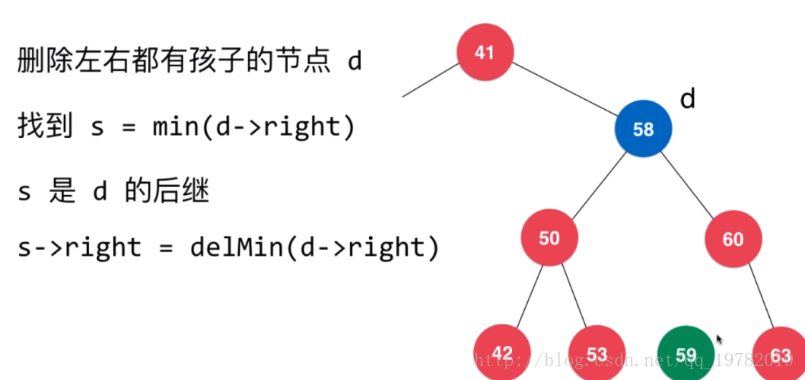
我们现在已经知道了如何去寻找一个替代的节点的方法,就让我们开始实践一下具
体的代码吧:(该种情况我们取右子树中的最小节点作为替代节点)
上面的代码我在来具体的解释一下找到替代节点后该如何完成删除操作。
我们找到了可以替代的节点为59节点,因此我们需要先复制一份59节点作为替代节点,
然后我们在用最开始写的删除树中的最小值并返回新树根地址的removemin()函数去
删除右子树中的最小值,然后在把新树根的地址赋值给“复制节点”作为其新的右孩子,
而“复制节点”的左孩子就是将要被删除的58节点原来的左孩子,我们只需要把58节点的
左子树的根地址赋值给“复制节点”的左孩子就好了,此时“复制节点”就应经完成了应有
的连接操作,我们就可以放心的把58节点给直接删除了,接着更新计数器,把“替代节点”
作为新树的根节点返回给上一层去连接使用。
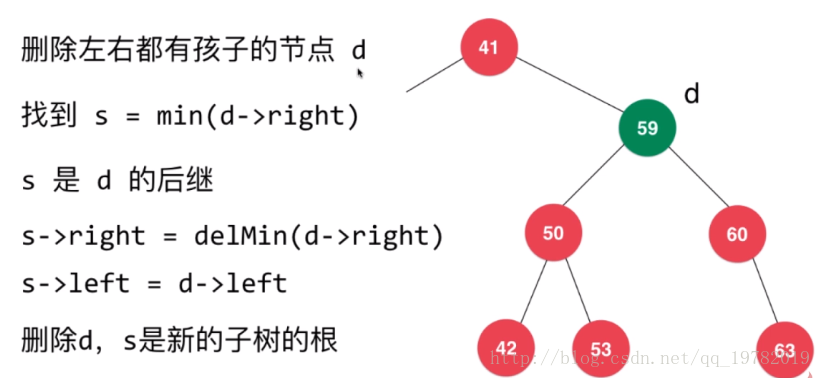
以下是测试函数:
测试结果如下:
3 1 5 2
delete the min:
3 2 5
delete the max:
3 2
delete the 3
2
如果想要获取二叉树所有的完整代码,请点击此处进入GitHub代码仓库。
首先,我们先来研究一下稍微简单一点的问题,如何删除二叉树中的最小值和最大值。

例如上图的这一棵二叉树中,最小值节点和最大值节点都在哪里呢?我们可以很清楚的从图中看出,13是该树的最小节点,42是该树的最大节点,且13节点位于树的最左边,而42位于树的最右边,这难道是一种巧合吗?当然不是,首先,让我们来回忆一下二叉树的一个非常重要的性质。
二叉树根节点的左子树都比根节点小,右子树都比根节点大。
也就是说,对于根节点28来说,他的左子树都比28小,右子树都比28大。那么我们就看28的左子树中的根16,而16又是一颗二叉树的根节点,根据二叉树根节点的左子树都比根节点小,右子树都比根节点大的原则,13比16小,22比16大,因此到13节点了,但是13节点左子树为空,也就是说没有节点比13还要小了,那么13就是这颗二叉树中的最小的节点了,同理,二叉树的最大的节点也可以很容易的得出了。
先从简单的问题开始,让我们来先讨论一下如何找到一颗二叉树的最小节点吧。
通过上面的讨论,我们已经了解到了一棵二叉树的最小值节点位于这颗树的“最左边”,最大节点位于这棵树的“最右边”,因此我们可以很容易的写出一个查找二叉树中最小节点的方法,代码如下所示:
// 返回以node为根的二分搜索树的最小键值所在的节点
node* minmum(node* node){
if( node->left == NULL )//如果该节点不存在左子树了,那么该节点就是这课树的最小节点
return node;
return minmum(node->left);//如果该节点还存在左子树,说明该节点并不是最小节点//则必须继续往它的左子树搜索下去(运用递归的方法) }上面的代码理解起来其实很简单,就是通过一个简单的递归,不停的从二叉树的树根开始,一直往树根的左子树搜索,直到被搜索的节点不存在左子树了,那么这个节点就肯定是这棵二叉树中的最小节点了。如果你还不明白为什么的话,请大念下面的这句话三遍!!!
二叉树根节点的左子树都比根节点小,右子树都比根节点大。
二叉树根节点的左子树都比根节点小,右子树都比根节点大。
二叉树根节点的左子树都比根节点小,右子树都比根节点大。
重要的事情说三遍!!上面这句话概括了这个算法的核心思想。
对于查找一棵树的最大节点,同理代码如下:
// 返回以node为根的二分搜索树的最大键值所在的节点
node* maximum(node* node){
if( node->right == NULL )//如果该节点没有右子树了,说明为最大的节点
return node;
return maximum(node->right);//该节点还存在右子树的话,说明还有比它更大的节点存在//因此该节点肯定不是最大节点,我们还要往“右边”搜索 }
现在我们知道了如何查找到一颗树中的最小节点和最大节点了,那么要删除这个节点该怎么做呢?
这个时候,我们就要分情况一个一个讨论了。
例如我们拿下面的这棵二叉树来讨论:

首先,我们可以很清楚的找到这棵二叉树的最小节点是13节点,我们要删除它直接delete掉这个节点就好了,接下来,15是最小节点,我们也delete掉,然而,对于接下来的最小节点22来说,这个节点貌似就不是这么简单的就能够删除了。
如果我们直接把22节点给delete掉,我们来看一下会发生什么样的问题。

虽然22节点成功删除了,但是,22的右子树却也因为22节点的删除而与原来的二叉树给“断开了”,那么这是失败的一次删除,因为我们在删除22节点的同时,还破坏了这棵树的完整性。那么,我们有什么好的办法呢?
办法当然是有的,首先,虽然22节点被删除了,但是22节点虽然没有左子树了,但是它的右子树我们不能“丢弃”人家,我们要让它重新与原来的树给连接起来,那么对于这段“被丢弃”的右子树的树根来说,我们想一想它具有什么特点呢?33节点能完美的替代被删除的22节点的位置吗?能不能替代,在二叉树中就是判断这两个节点在树中的“状态”是不是一样的。对于被删除的22节点来说,22节点比它的根节点41小,且小于它的左子树,大于它的右子树。而对于“被丢弃”的右子树的树根节点33来说,因为它也处于树根节点41的的子树中,也就是它比根节点41小,而且本来满足它比它的左子树小,右子树大的特点,因此我们发现,33节点与被删除的22节点此时代表的是完全的一样的,因此我们只要把33节点的地址返回给上一层节点(41节点),作为其新的左孩子,这样,我们不仅把22节点成功删除了,而且也使得22节点的右子树没有被“抛弃”,并且重新和原来的树组合起来,完美的符合了二叉树的结构特点。那么就让我们来看一下具体的代码吧。
//删除rootnode为根的二叉树的最小值,并且把删除后的树的地址返回
node*removemin(node*rootnode){
if(rootnode->left==NULL){//遍历到了树中最左边的节点,也就是该树中最小的节点
node*rightroot=rootnode->right;//把要删除的节点的右子树根节点的地址保存好
delete rootnode;//需要先记录右子树地址在删除节点,否则先删除节点则丢失了右子树根节点的地址
count--;
return rightroot;//把右子树的根地址返回到上一层以供连接使用
}
rootnode->left=removemin(rootnode->left);//连接记录好的右子树的根地址,重组为父节点的左子树
return rootnode;
}其中的参数rootnode第一次代表的是需要本删除最小节点的树根地址,后面每次递归中的rootnode都为本层节点的地址。
同理,删除树中最大节点的代码如下:
// 删除以rootnode为根的二叉树的最大节点,并把新树的根节点返回
node*removemax(node*rootnode){
if(rootnode->right==NULL){//遍历到了树中最大节点的位置
node*leftnode=rootnode->left;//保存住被删除节点左子树的根节点地址
delete rootnode;//需要先记录左子树地址在删除节点,否则先删除节点则丢失了左子树根节点的地址
count--;
return leftnode;//返回上一级做连接使用
}
rootnode->right=r
de0e
emovemax(rootnode->right);//连接被脱离的子树
return rootnode;//返回当前节点的地址
}好了,现在我们已经能够很轻松实现删除一棵以root为根的二叉树的最小值和最大值,并且把新树的根地址返回的方法了。那么,让我们现在来继续往更深入的探讨一下,如何删除二叉树中的任意一个节点呢?
让我们想一想,在二叉树中的每一棵节点,存在哪几种状态呢?
1.无左子树,无右子树。
2.无左子树,有右子树。
3.有左子树,无右子树。
4.既有左子树,也有右子树。
因此,我们在删除树中的一个节点来说,也要去分情况讨论了。
1.无左子树,无右子树。
这种情况很简单,我们只要删除该节点,并且返回一个NULL值给上一层节点做连接使用(可能是被连接到上一层节点的左子树也可能是右子树),但是都不影响二叉树的结构。
1.无左子树,有右子树。
此时这种情况就和我们删除一棵树中的最小节点的处理方法类似了。我们只需要先把被删除节点的右子树信息(右子树根地址)给保存下来以备上一层连接使用,然后在去删除该节点(顺序不能反,否则先把节点删除了,则也丢失了该节点右子树的信息,右子树也一起消失了)。
3.有左子树,无右子树
此时这种情况就和我们删除一棵树中的最大节点的处理方法类似了。我们只需要先
把被删除节点的左子树信息(左子树根地址)给保存下来以备上一层连接使用,然后在
去删除该节点(顺序不能反,否则先把节点删除了,则也丢失了该节点左子树的信息,
左子树也一起消失了)。
4.既有左子树,也有右子树。
这种情况是最复杂的,处理起来也是最难的。:

假设我们要删除58这个节点,但是58既有左子树,也有右子树,那么我们应该选择哪一
个节点作为“替代节点呢”?上面我们讨论了删除只含有单边子树情况是如何挑选替代节点
就是其左子树或右子树的树根作为替代节点(也就是该节点的左孩子或者右孩子)。然而,
此时我们这个节点既含有左子树也还有右子树,那么该选哪个孩子作为节点呢?是50节点
还是56节点呢?答案是哪个孩子节点都不选。因为他们都不符合58节点所处的“状态”。
那么58节点此时的状态是怎怎样的呢?还是回到我们对于二叉树结构的定义上:二叉
树根节点的左子树都比根节点小,右子树都比根节点大。
我们发现,58节点比它左子树所有的节点都要小,比它右子树所有节点都要大。那么,假设我们让左孩子50替代58的位置,我们来看一看,50确实是比58的右子树所有的节点都要小,但是50却并不比58左子树的所有节点都要大,比如其中的53节点就要比50大,因此50节点肯定是不符合二叉树结构的特点的,也就不能去代替58节点的位置了。那么我们再来看一下58的右孩子60能否替代58节点的位置呢?如果60替代58节点的位置,原来58节点的左子树的所有节点确实比60要小,满足左子树的关系,但是58的右子树的所有节点却并不是都比60大,比如其中的59节点。因此58的右孩子60节点也不能够完美的胜任这个任务。
那我我们应该选择哪一个节点作为替代节点呢?我们发现,作为替代节点必须满足的条件是:
二叉树根节点的左子树都比根节点小,右子树都比根节点大。
因此,我们需要找58节点的替代节点,因为58节点的左子树所有节点都比58小,所以如
果我们在58左子树中找到一个最大的节点作为替代节点。则这个节点我们发现比58左子
树的所有节点都要大,而且一定是比58节点的右子树所有节点都要小的(因为该节点位
于58节点的左子树,所以肯定比58节点的右子树所有节点都要小,二叉树的结构定义)。
此时,肯定有些聪明的同学会想到了,我们在58右子树中找到一个最小节点作为替
代节点。这样寻找替代节点也是可行的,一样是符合二叉树的结构定义的。右子树的最
小节点本身就比右子树所有节点要小,然后根据二叉树的结构特点也能够很轻松的得出
要比左子树所有的节点都要大的。接下来我们以右子树的最小节点作为替代节点来讨论

我们现在已经知道了如何去寻找一个替代的节点的方法,就让我们开始实践一下具
体的代码吧:(该种情况我们取右子树中的最小节点作为替代节点)
/*
* 删除以node为根的二叉树中的Key为key的节点
* 并且返回新二叉树的根地址
*/
node* remove(node*Node,Key key){
if(Node==NULL){//如果树为空的话
return NULL;//返回空值
}
else if(Node->key==key){//此时找到了需要被删除的节点
if(Node->left==NULL){//待删除节点的左子树为空的话,右子树为空或者不为空都不影响
node*rightnode=Node->right;//把右子树的根地址保存下来
delete Node;//节点此时可以被删除了
count--;//更新计数器
return rightnode;//右子树为空的话,返回NULL,不为空的话,返回右子树的根节点
}
else if(Node->right==NULL){//此时待删除节点的右子树为空的话,左子树为空或者不为空都不影响
node*leftnode=Node->left;//记录左子树的根地址,可能为空也可能为一个值,但不影响
delete Node;//此时可以删除节点
count--;//更新计数器
return leftnode;//左子树为空的话,返回NULL,不为空的话,返回左子树的根节点
}
else{//此时待删除节点的左右子树均不为空的话
//替换节点可以是该节点右子树中的最小值或者左子树的最大值,这里我们选右子树中的最小值作为替换
node*replacenode=new node(minmum(Node->right)) ;//复制待删除节点右子树的最小节点作为替换节点
count++;//增加计数器
replacenode->right=removemin(Node->right);//删除待删节点的右子树的最小值并把新树的根地址再重新赋值给替代
//节点的右子树
replacenode->left=Node->left;//替代节点的左子树就是原来节点的左子树
delete Node;//替代节点的左右子树都已经更新完毕了,可以删除了
count--;//更新计数器
return replacenode;//返回替代节点的地址即新树的根节点地址给上一层连接用
}
}
}上面的代码我在来具体的解释一下找到替代节点后该如何完成删除操作。
我们找到了可以替代的节点为59节点,因此我们需要先复制一份59节点作为替代节点,
然后我们在用最开始写的删除树中的最小值并返回新树根地址的removemin()函数去
删除右子树中的最小值,然后在把新树根的地址赋值给“复制节点”作为其新的右孩子,
而“复制节点”的左孩子就是将要被删除的58节点原来的左孩子,我们只需要把58节点的
左子树的根地址赋值给“复制节点”的左孩子就好了,此时“复制节点”就应经完成了应有
的连接操作,我们就可以放心的把58节点给直接删除了,接着更新计数器,把“替代节点”
作为新树的根节点返回给上一层去连接使用。

以下是测试函数:
int main()
{
BST<int,int> a=BST<int,int>();
a.insert(3,4);
a.insert(1,4);
a.insert(5,4);
a.insert(2,4);
a.leverorder();
a.removemin();
cout<<endl;
cout<<"delete the min:"<<endl;
a.leverorder();
cout<<endl;
a.removemax();
cout<<"delete the max:"<<endl;
a.leverorder();
cout<<endl<<"delete the 3"<<endl;
a.remove(3);
a.leverorder();测试结果如下:
3 1 5 2
delete the min:
3 2 5
delete the max:
3 2
delete the 3
2
如果想要获取二叉树所有的完整代码,请点击此处进入GitHub代码仓库。
相关文章推荐
- 排序二叉树常规操作(搜索,插入,删除,最大节点,最小节点)
- 二分搜索树的实现以及各种操作(支持重复节点)
- 二分搜索树非递归节点计数删除
- 5-8 二分搜索树的删除,删除一个节点的步骤2
- 挖掘算法中的数据结构(七):二分搜索树(删除、广度优先遍历、顺序性)及 衍生算法问题
- ZooKeeper_6_Java操作ZK_删除节点
- DOM删除节点的操作
- (转载)html dom节点操作(获取/修改/添加或删除)
- 删除没有头结点的链表指点节点操作
- javascript 原生方法对dom节点的操作,创建、添加、删除、替换、插入、复制、移动等操作
- Magicodes.WeiChat——ASP.NET Scaffolding生成增删改查、分页、搜索、删除确认、批量操作、批量删除等业务代码
- html dom节点操作(获取/修改/添加或删除)
- C#中对 XML节点进行添加,删除,查找和删除操作
- 链表循环保留M个节点 然后删除N个节点 重复操作到链表尾部
- DOM高级应用——表格元素的添加、删除、搜索操作1
- 简单的XML文件操作(xml文件生成,节点追加、遍历、修改、删除)
- c# 操作xml文件(插入节点、修改、删除)
- JS常见DOM节点操作示例【创建 ,插入,删除,复制,查找】
- js操作之动态添加,删除节点
- C#域控操作大全_节点删除_修改密码_添加用户
