【机器学习系列之四】概率统计学习基础
2017-11-01 12:28
549 查看
这部分介绍概率里的重要概念,如随机事件,贝叶斯概率公式。
统计里描述数据分布的重要概念如期望,方差,众数,四分位数。
统计推断里的参数估计
频率:以抛硬币为例,重复抛十次,若出现4次正面,6次反面。
记A:出现正面 B:出现反面
事件A的频率为:P(A) = 4/10 其中4称为事件A的频数。
概率:使用频率的稳定值作为该事件的概率近似值
条件概率:P(色盲患者|女性) = p(女性,且是色盲患者)/p(女性)
该公式说明的是:某人为女性,那么她是色盲患者的概率是多少,换成公式可以表示为:
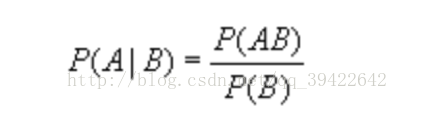
事件独立性:事件A的发生与事件B是否发生无关,则称两个事件是独立的。若事件A,事件B独立,则有P(AB) = P(A)*P(B),这个性质在朴素贝叶斯算法会用到。
全概率公式:P(色盲患者) = P(女性)*P(是女性,且是色盲患者) + P(男性)*P(是男性,且是色盲患者)。
全概率公式的思想就是:将事件A分解成几个小事件,然后相加从而求得事件A的概率。
换成公式可表示为:
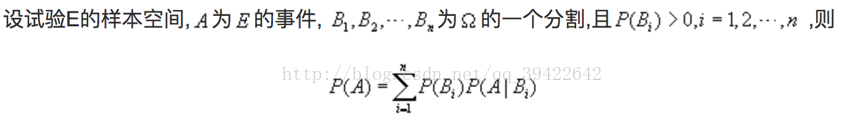
贝叶斯公式:与全概率公式解决问题相反,贝叶斯公式建立在条件概率的基础上,用来寻找事件发生的起因。如图:

在知道某人为色盲患者,那么他可能是男性,也可能是女性,通过这条公式,可以推断出该患者是女性的概率,与是男性的概率。
他的核心思想是:通过结果,推断导致该结果的原因。用数学公式表示为:
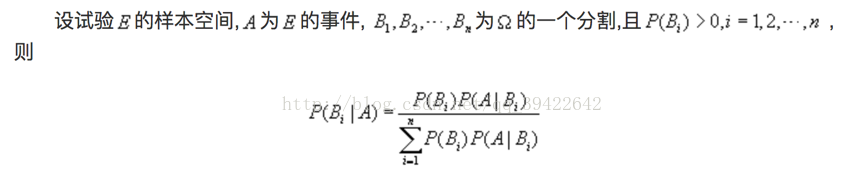
算数平均值:是表征数据集中趋势的一个统计指标。它是一组数据之和,除以这组数据个数/项数。
优点:它较中位数、众数更少受到随机因素影响,缺点是它更容易受到极端值影响。
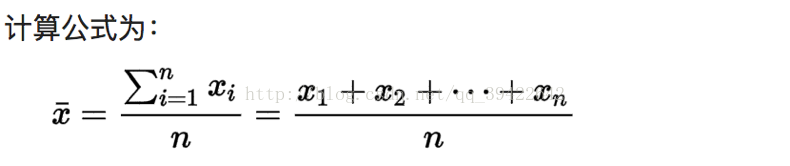
加权平均值:
适用于对分组后的数据求均值,通过各组标志值与各组频数相乘的总和除以各组频数之和得到。

中位数:是指一组数据按照大小排列后,处于中间位置上的变量值。它是集中趋势的反映。
众数:一组数据出现次数最多的变量值
极差:一组数据的最大值,最小值的差。该标准未考虑数据的分布情况,易受极端值的影响。
方差与标准差:它反映了每个数据与其平均数相比平均相差的数值。

对方差开根号就是标准差,它有计量单位且与变量值相同,因此它的实际意义要比方差清楚,但对社会经济现象进行分析时,更多地使用标准差作为衡量标准。
四分位距:由图示,可以算出四分差的距离为 115 − 105 = 10.
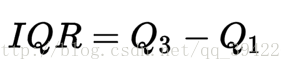

变异系数:也称离散系数,用CV值表示,是标准差与均值之比。其值越大,离散程度越大。
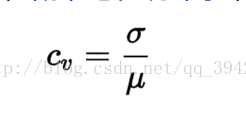
常用样本中的某些值来表征总体的特性:如样本均值,样本方差,样本标准差。
样本均值:样本均值不是稳健统计,容易受一场点影响。它是随机向量{\displaystyle \textstyle \mathbf {X} }X平均数的无偏估计
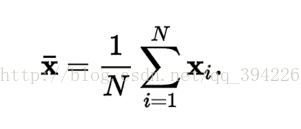
概率密度函数:是一个描述这个随机变量的输出值,在某个确定的取值点附近的可能性的函数。而随机变量落在某个区域之内的概率为密度函数在该区域上的积分。

累积分布函数:它是概率密度函数的积分。能完整的描述一个实随机变量X的概率分布。

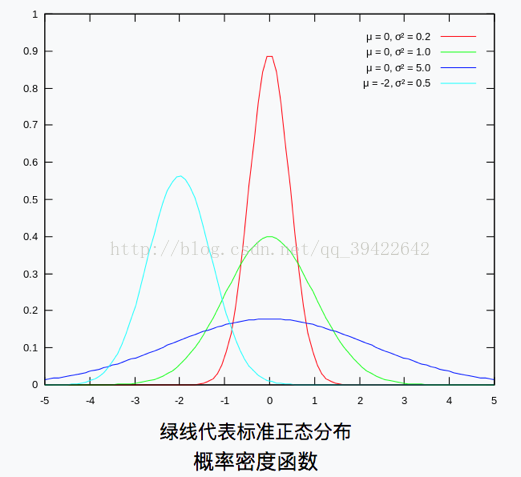
正太分布:这个分布函数具有非常好的特性,使得它在诸多统计学科,离散科学方面都有着不可替代的影响力。比如,图像处理中最常用的滤波器类型就是高斯滤波器。(也就是所谓的正太分布函数)。
它的概率密度函数为:

它的概率密度函数图如下:
数学期望:它是实验中每次可能结果的概率乘以其结果的总和。它反映了随机变量平均取值的大小。用公式表示如下:
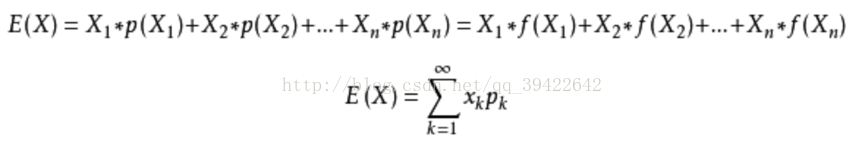
方差:用来衡量随机变量或一组数据离散程度的度量,即它是度量随机变量与期望(均值)之间的偏离程度。总体方差的计算公式为:
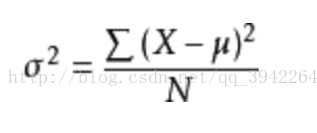
其中X为每个样本值,表示期望,N为样本个数。
点估计:对某一统计量的估计,常用的方法有距估计,极大似然估计。
1.矩估计:它的主要思想是通过样本矩及其函数,替换相应的总体矩及其函数,即替换原理。
例:要估计某一地区的平均收入(总体),可以在该地区随机选取1万人(样本),计算他们的平均收入,然后把这一万人的平均收入近似作为该地区的平均收入。
常用的参数估计有:
用样本均值估计总体均值EX,
用样本方差估计总体方差DX,
用样本k阶原点矩估计总体EXk,
用样本的 p 分位数估计总体的 p 分位数,
用样本中位数估计总体中位数。
2.极大似然估计:它的使用条件是在总体分布已知的情况下的参数估计法。“似然”=“看起来像“,因而它的基本思想就是似然原理:选择导致某“结果”发生可能性最大的“原因”,作为似然原因。
例如:有人打靶,打中了10环,它最可能是由教练打的,而不是新手打的。
(1)若总体X为离散型,其概率分布列为:

其中为未知参数,设(X1,X2,···,Xn)的一组观测值为(x1,x2,x3,···,xn),易知样本X1,X2,···,Xn取到观测值x1,x2,···,xn的概率为:
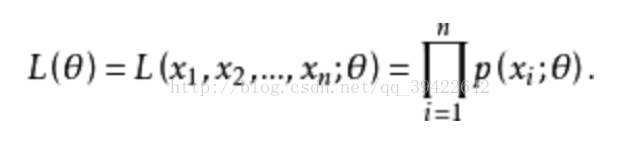
这一概率随 的取值而变化,它是 的函数,称 为样本的似然函数。
(2)若总体X为连续型,其概率密度函数为:f(x,)。故它的似然函数为:
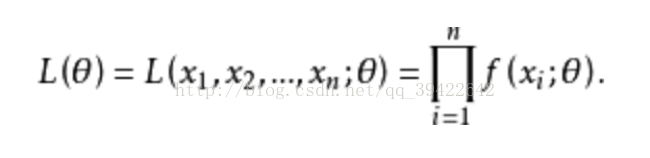
该式子就是似然函数,对似然函数求极值点,可得概率取最大时,的取值。
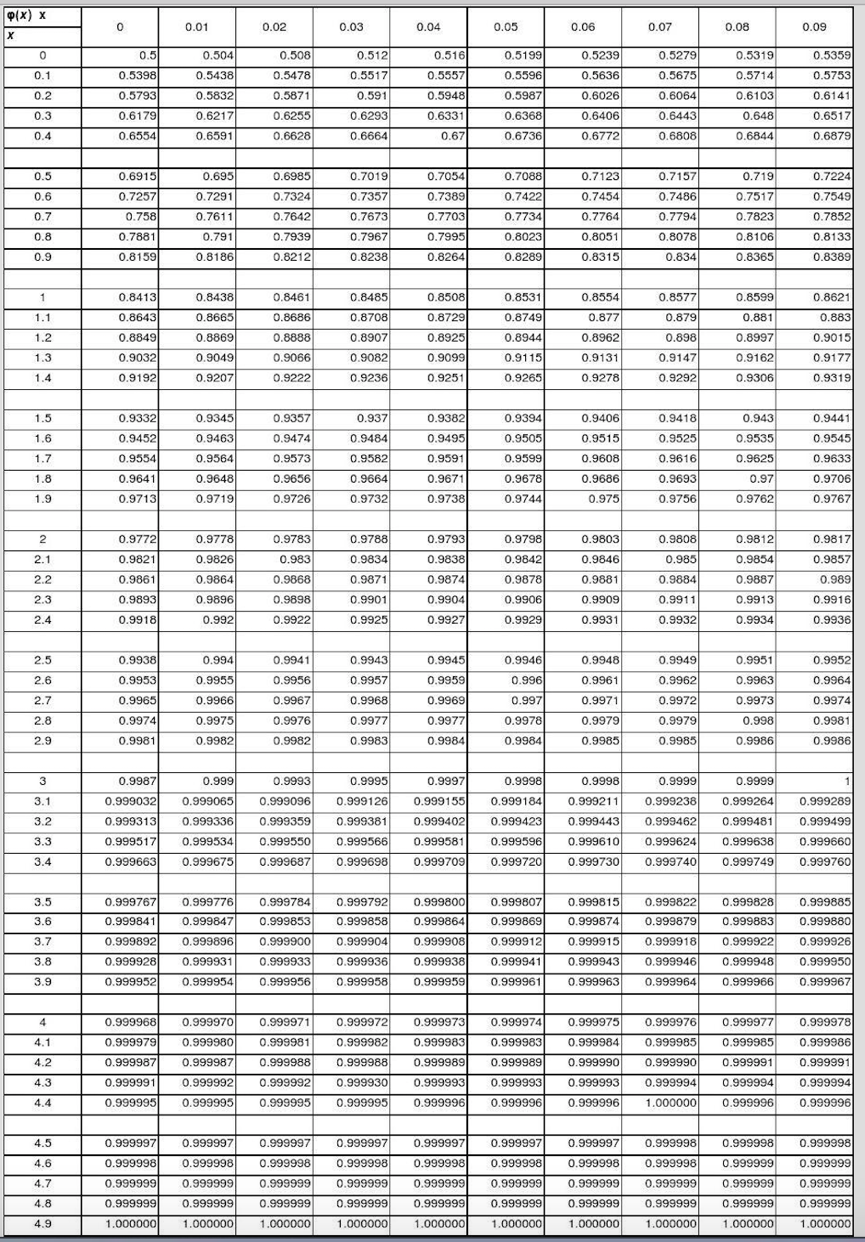
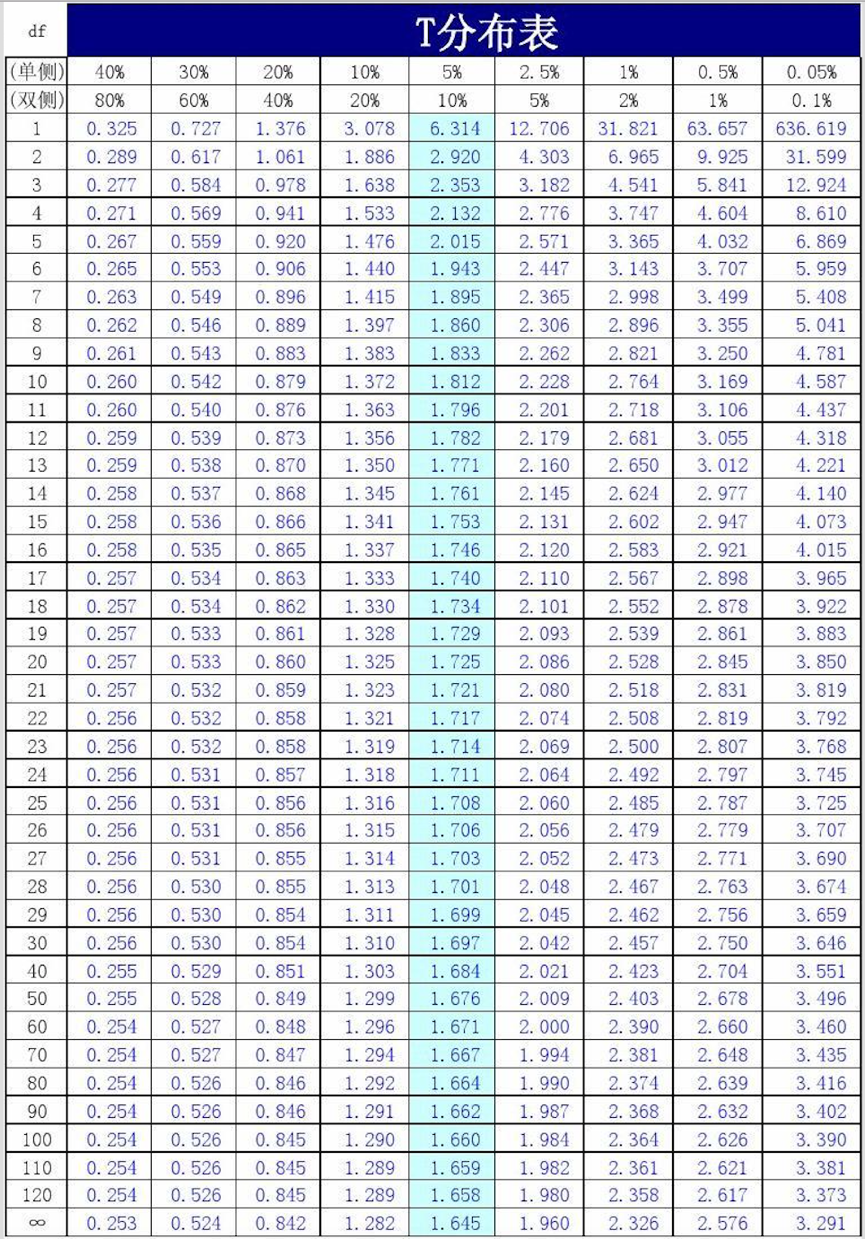
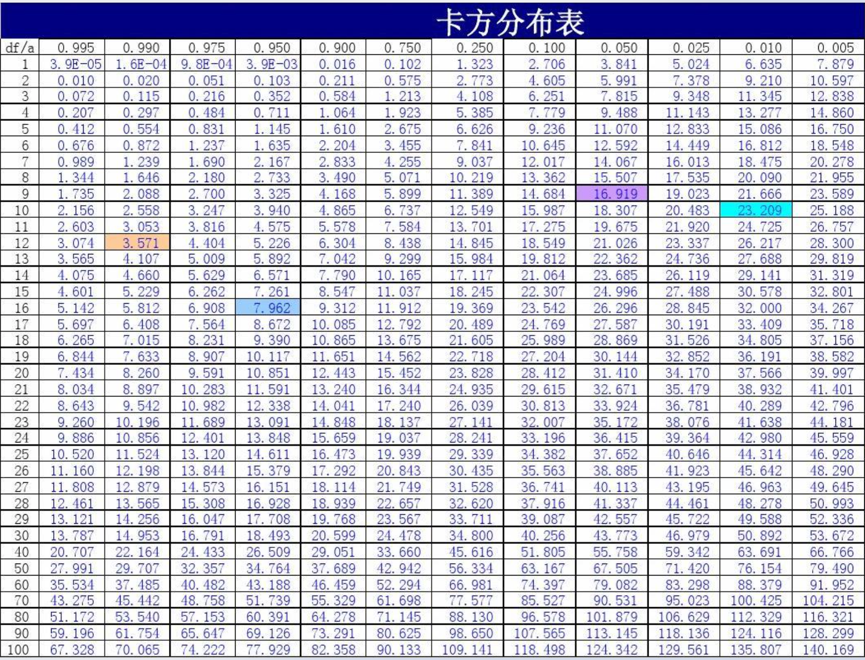
常用分布表
标准正太分布表
统计里描述数据分布的重要概念如期望,方差,众数,四分位数。
统计推断里的参数估计
3.1 概率
随机事件:某一事件可能发生,也可能不发生,则称其为随机事件频率:以抛硬币为例,重复抛十次,若出现4次正面,6次反面。
记A:出现正面 B:出现反面
事件A的频率为:P(A) = 4/10 其中4称为事件A的频数。
概率:使用频率的稳定值作为该事件的概率近似值
条件概率:P(色盲患者|女性) = p(女性,且是色盲患者)/p(女性)
该公式说明的是:某人为女性,那么她是色盲患者的概率是多少,换成公式可以表示为:
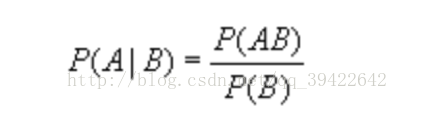
事件独立性:事件A的发生与事件B是否发生无关,则称两个事件是独立的。若事件A,事件B独立,则有P(AB) = P(A)*P(B),这个性质在朴素贝叶斯算法会用到。
全概率公式:P(色盲患者) = P(女性)*P(是女性,且是色盲患者) + P(男性)*P(是男性,且是色盲患者)。
全概率公式的思想就是:将事件A分解成几个小事件,然后相加从而求得事件A的概率。
换成公式可表示为:
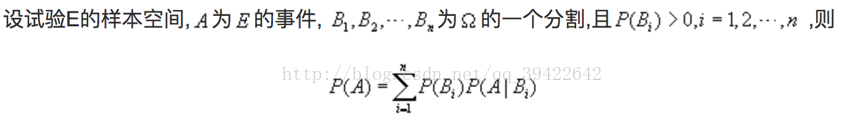
贝叶斯公式:与全概率公式解决问题相反,贝叶斯公式建立在条件概率的基础上,用来寻找事件发生的起因。如图:

在知道某人为色盲患者,那么他可能是男性,也可能是女性,通过这条公式,可以推断出该患者是女性的概率,与是男性的概率。
他的核心思想是:通过结果,推断导致该结果的原因。用数学公式表示为:
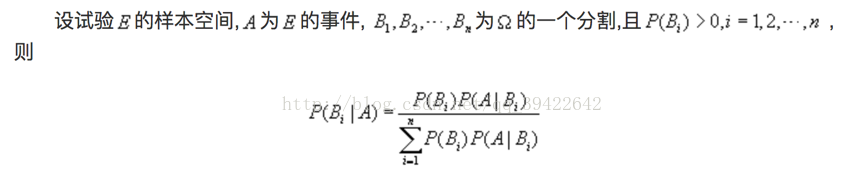
3.2 描述性统计
3.2.1集中趋势
集中趋势是指某一组数据向中心值靠拢的倾向,测度集中趋势就是寻找代表数据一般水平的代表值。常用的衡量标准有算术平均值,加权平均值,中位数,众数。算数平均值:是表征数据集中趋势的一个统计指标。它是一组数据之和,除以这组数据个数/项数。
优点:它较中位数、众数更少受到随机因素影响,缺点是它更容易受到极端值影响。
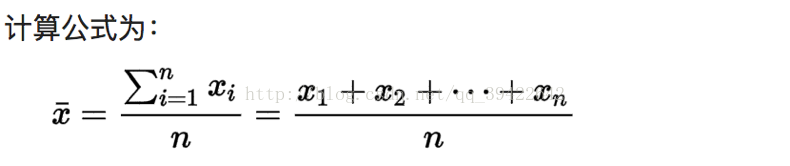
加权平均值:
适用于对分组后的数据求均值,通过各组标志值与各组频数相乘的总和除以各组频数之和得到。

中位数:是指一组数据按照大小排列后,处于中间位置上的变量值。它是集中趋势的反映。
众数:一组数据出现次数最多的变量值
3.2.2离散趋势
离散趋势是指反映一个变量远离其中心值的程度。数据的离散程度越大,集中趋势的测度值对该组数据的代表性就越差。极差:一组数据的最大值,最小值的差。该标准未考虑数据的分布情况,易受极端值的影响。
方差与标准差:它反映了每个数据与其平均数相比平均相差的数值。

对方差开根号就是标准差,它有计量单位且与变量值相同,因此它的实际意义要比方差清楚,但对社会经济现象进行分析时,更多地使用标准差作为衡量标准。
四分位距:由图示,可以算出四分差的距离为 115 − 105 = 10.
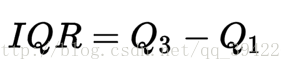

变异系数:也称离散系数,用CV值表示,是标准差与均值之比。其值越大,离散程度越大。
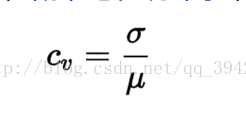
3.3 样本与总体
若研究对象很大,比如一个国家人民的生活水平,此时不能把一个国家的所有人都拿来研究,这时就用到了随机采样。通过样本,可以近似的推断总体的一些状况。为了研究方便,常用X表示总体,X的概率分布就表示了总体的中各个值的分布情况。常用样本中的某些值来表征总体的特性:如样本均值,样本方差,样本标准差。
样本均值:样本均值不是稳健统计,容易受一场点影响。它是随机向量{\displaystyle \textstyle \mathbf {X} }X平均数的无偏估计
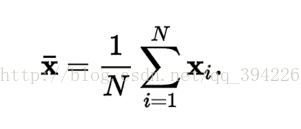
概率密度函数:是一个描述这个随机变量的输出值,在某个确定的取值点附近的可能性的函数。而随机变量落在某个区域之内的概率为密度函数在该区域上的积分。

累积分布函数:它是概率密度函数的积分。能完整的描述一个实随机变量X的概率分布。

正太分布:这个分布函数具有非常好的特性,使得它在诸多统计学科,离散科学方面都有着不可替代的影响力。比如,图像处理中最常用的滤波器类型就是高斯滤波器。(也就是所谓的正太分布函数)。
它的概率密度函数为:

它的概率密度函数图如下:

数学期望:它是实验中每次可能结果的概率乘以其结果的总和。它反映了随机变量平均取值的大小。用公式表示如下:
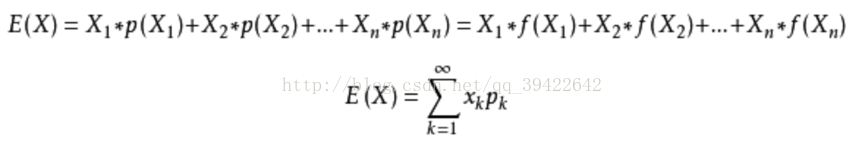
方差:用来衡量随机变量或一组数据离散程度的度量,即它是度量随机变量与期望(均值)之间的偏离程度。总体方差的计算公式为:
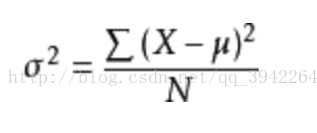
其中X为每个样本值,表示期望,N为样本个数。
3.4 统计推断
3.4.1参数估计
参数估计问题就是根据样本对未知参数,如数学期望,方差作出估计。常用的点估计和区间估计。点估计:对某一统计量的估计,常用的方法有距估计,极大似然估计。
1.矩估计:它的主要思想是通过样本矩及其函数,替换相应的总体矩及其函数,即替换原理。
例:要估计某一地区的平均收入(总体),可以在该地区随机选取1万人(样本),计算他们的平均收入,然后把这一万人的平均收入近似作为该地区的平均收入。
常用的参数估计有:
用样本均值估计总体均值EX,
用样本方差估计总体方差DX,
用样本k阶原点矩估计总体EXk,
用样本的 p 分位数估计总体的 p 分位数,
用样本中位数估计总体中位数。
2.极大似然估计:它的使用条件是在总体分布已知的情况下的参数估计法。“似然”=“看起来像“,因而它的基本思想就是似然原理:选择导致某“结果”发生可能性最大的“原因”,作为似然原因。
例如:有人打靶,打中了10环,它最可能是由教练打的,而不是新手打的。
(1)若总体X为离散型,其概率分布列为:

其中为未知参数,设(X1,X2,···,Xn)的一组观测值为(x1,x2,x3,···,xn),易知样本X1,X2,···,Xn取到观测值x1,x2,···,xn的概率为:
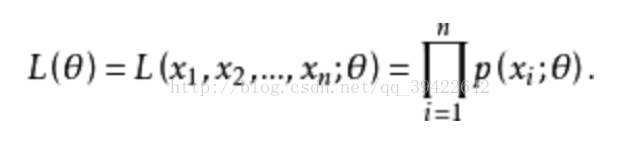
这一概率随 的取值而变化,它是 的函数,称 为样本的似然函数。
(2)若总体X为连续型,其概率密度函数为:f(x,)。故它的似然函数为:
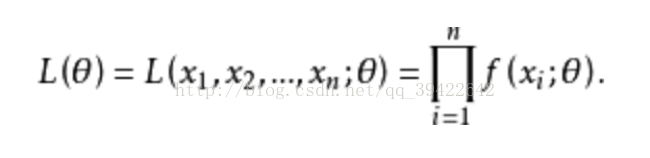
该式子就是似然函数,对似然函数求极值点,可得概率取最大时,的取值。
常用分布表
标准正太分布表



相关文章推荐
- 机器学习、大数据、深度学习、数据挖掘、统计、决策和风险分析、概率和模糊逻辑的常见问题解答
- 机器学习、大数据、深度学习、数据挖掘、统计、决策和风险分析、概率和模糊逻辑的常见问题解答
- 深度学习之数学基础(概率与统计)
- 机器学习(一)- 数学基础之统计概率
- 统计基础学习4--概率
- 【ML学习笔记】2:机器学习中的数学基础2(琴生不等式,概率公式,统计量)
- 统计基础学习4--概率
- 福利 | Intel发布AI免费系列课程3部曲:机器学习基础、深度学习基础以及TensorFlow基础
- 机器学习之数学基础(概率与统计推断、矩阵、凸优化)
- 机器学习、大数据、深度学习、数据挖掘、统计、决策和风险分析、概率和模糊逻辑的常见问题解答
- 机器学习的概率与统计知识复习总结
- aauto学习系列之<3>:基础语法1
- Linux运维系统工程师与java基础学习系列-4
- 【算法系列学习】[kuangbin带你飞]专题十二 基础DP1 C - Monkey and Banana
- 零基础学习在Android进行SDL开发系列文章
- CUDA系列学习(五)GPU基础算法: Reduce, Scan, Histogram
- Android基础之AdapterView系列学习
- http协议学习系列之一——基础概念篇
- 一步一步学习sharepoint2010 workflow 系列第二部分:SharePoint无代码工作流 第7章 自定义表单的基础知识(Custom form fundamentals)
- C++基础学习系列--1、1的简陋版本--输入输出流与字符串变量的使用
