基于图像形状的一种比较漂亮的分类算法

基于图像形状的一种比较漂亮的分类算法

我首先讲一下我所遭遇到的情况吧:

有n类似于下图的图片:



我这里有一个需求就是,将这些图片分类,分类的效果至少也应该是这样的:



将一些形状非常类似的图片分在一起.

我大致查阅了一下挺多的分类算法,这些算法大致分为了两类:

一类是通过对分类器进行训练,比如说要识别猫,那就要喂给分类器非常多的猫的图片,得到一些参数之后才能够比较精确地对图片进行识别.当然,这一大类的方法对于我们所拥有的数据来说,并不适合,我们并没有用于训练的图片.

另外一种方法不用训练,思想和机器学习里面的聚类差不太多,主要通过比较图片的一些特征,计算出与相似度类似的一个度量,来对图片进行分类.

好吧,我们大致只能使用聚类之类的东西来分类了.

究竟怎么来分呢?

说实话,我尝试了一些比较有名的聚类算法,效果都不怎么理想,然后我看到了Hausdorff Distance,这是一种在图像处理中轨迹识别什么的经常用到的距离度量,我只是抱着试一试的心态尝试了一下[b]Hausdorff
Distance加上k均值聚类,结果效果出乎我的意料,效果拔群.上面的效果你也看到了,至少在眼睛上看起来,非常不错.[/b]

[b]关于[b]Hausdorff Distance,推荐你看这里:[/b][/b]

[b]http://cgm.cs.mcgill.ca/~godfried/teaching/cg-projects/98/normand/main.html
[/b]

有中文翻译版的:

http://blog.sina.com.cn/s/blog_4062094e0102vkpf.html


k均值聚类应该不用我来讲了,差不多都烂了.

我这里给出Hausdorff Distance的Python代码实现吧:

[python] view
plain copy

 print?

  

[python] view
plain copy

 print?

""" 

    目标: 

    ~~~~~~~~~ 

    实现 Hausdorff 距离.该距离的定义如下: 

    A = {a1, a2, ..., an}, B = {b1, b2, ..., bm} 

    两者的 Hausdorff 距离为: 

    H(A, B) = max{h(A, B), h(B, A)}, 

    其中 

    h(A, B)的定义如下,无法用数学公式来展现,我这里用语言来描述一下得了. 

    对于A中的每一个点a,首先在B中找到一个距离a最近的点b,得到a,b它们之间的距离dist(a, b),这里的dist定义如下: 

    dist(a, b) = sqrt((xa - xb)^2, (ya - yb)^2),就是欧氏距离啦. 

    通过计算得到n个这样的距离,找出其中最大的一个,作为h(A, B),h(B, A)同理. 

"""  

from math import sqrt  

  

def euclidean_metric(pa, pb):  

    ''''' 

    计算两个点的欧式距离. 

    关于输入的pa以及pb,它们应该是一个list或者tuple,长度应该相等. 

    '''  

    return sqrt((pa[0] - pb[0])**2 + (pa[1] - pb[1])**2)  

  

def one_way_hausdorff_distance(sa, sb):  

    '''''计算单向hausdorff距离'''  

    distance = 0.0  

    for pa in sa: # 对于a集合中的每一个点,要求出这个点到  

        shortest = 9999999  

        for pb in sb:  

            dis = euclidean_metric(pa, pb)  

            if dis < shortest:  

                shortest = dis  

        if shortest > distance:  

            distance = shortest  

    return distance  

  

def hausdorff_distance(sa, sb):  

    ''''' 

    计算两个集合中的点的 hausdorff 距离. 

    关于输入的sa以及sb,两者应该是点的list或者tuple,而点的定义参照euclidean_metric. 

    '''  

    dis_a = one_way_hausdorff_distance(sa, sb)  

    dis_b = one_way_hausdorff_distance(sb, sa)  

    return dis_a if dis_a > dis_b else dis_b  

  

  

if __name__ == '__main__':  

    assert(euclidean_metric((1, 1), (1, 6)) == 5)  

    A = [(0, 0), (1, 0), (2, 0), (3, 0), (4, 0)]  

    B = [(0, 3), (1, 3), (2, 3), (3, 3), (3, 2), (4, 2)]  

    C = [(4, 2), (4, 1), (4, 0)]  

    D = [(0, 2), (1, 2), (2, 2), (2, 3), (2, 4)]  

    one_way_hausdorff_distance(A, B)  

另外还有一种度量公式,那就是Fréchet distance.

这是最近才找到的一种距离,将这种距离运用于分类,效果其实比上面的还要好.

它的python实现代码如下:



[python] view
plain copy

 print?

""" 

    Fréchet distance 

"""  

import math  

import numpy as np  

  

# Euclidean distance.  

def euc_dist(pt1,pt2):  

    return math.sqrt((pt2[0]-pt1[0])*(pt2[0]-pt1[0])+(pt2[1]-pt1[1])*(pt2[1]-pt1[1]))  

  

def _c(ca,i,j,P,Q):  

    if ca[i,j] > -1:  

        return ca[i,j]  

    elif i == 0 and j == 0:  

        ca[i,j] = euc_dist(P[0],Q[0])  

    elif i > 0 and j == 0:  

        ca[i,j] = max(_c(ca,i-1,0,P,Q),euc_dist(P[i],Q[0]))  

    elif i == 0 and j > 0:  

        ca[i,j] = max(_c(ca,0,j-1,P,Q),euc_dist(P[0],Q[j]))  

    elif i > 0 and j > 0:  

        ca[i,j] = max(min(_c(ca,i-1,j,P,Q),_c(ca,i-1,j-1,P,Q),_c(ca,i,j-1,P,Q)),euc_dist(P[i],Q[j]))  

    else:  

        ca[i,j] = float("inf")  

    return ca[i,j]  

  

""" Computes the discrete frechet distance between two polygonal lines 

Algorithm: http://www.kr.tuwien.ac.at/staff/eiter/et-archive/cdtr9464.pdf 

P and Q are arrays of 2-element arrays (points) 

"""  

def frechet_distance(P,Q):  

    ca = np.ones((len(P),len(Q)))  

    ca = np.multiply(ca,-1)  

    return _c(ca,len(P)-1,len(Q)-1,P,Q)  

函数的调用方法和上面Hausdorff Distance的代码一致.
下面是路径相似性描述：Fréchet
distance的知乎的介绍：
https://zhuanlan.zhihu.com/HicRhodushicsalta/20159963

路径相似性描述：Fréchet distance

Owl
of Minerva


2 年前

Fréchet distance(弗雷歇距离)是法国数学家Maurice
René Fréchet在1906年提出的一种路径空间相似形描述( 此外还在这篇论文里定义了 度量空间)，这种描述同时还考虑进路径空间距离的因素[1]，对于空间路径的相似性比较适用。

直观的理解，Fréchet distance就是狗绳距离：主人走路径A，狗走路径B，各自走完这两条路径过程中所需要的最短狗绳长度。


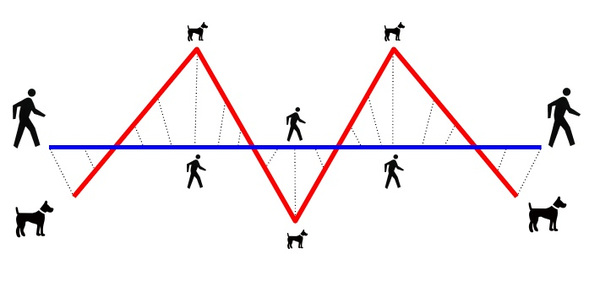
严格的数学定义如下：
设二元组

是一个度量空间，其中

是

上的度量函数.
1. 在单位区间

上的映射

是连续映射，则称

为

上的连续曲线。
2. 从单位区间到其自身的映射

，满足如下三个条件：1)

是连续的，2)

是非降的，即对于任意

，且

，都有

成立，3)

是满射，则称函数

为单位区间

的重参数化函数，且此时有

，

.
特别地，当

为恒等函数

时，称

为平凡重参数化函数，否则，称

为非平凡重参数化函数。显然的，单位区间的重参数化函数有无穷多个。
3. 设

和

是

 上的两条连续曲线，即

，

.
又设 α 和 β 是单位区间的两个重参数化函数，即 

，

.
则曲线

与曲线

的弗雷歇距离

定义为


其中

是

上的度量函数.
数字化/离散化


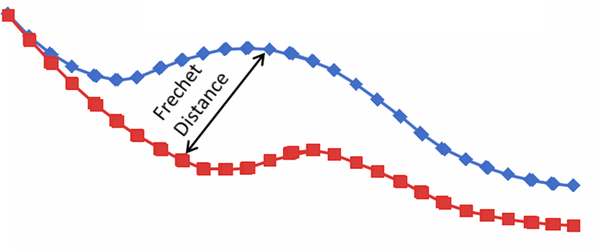
设定

是时间点，该时刻，曲线

上的采样点为

,
曲线

上采样点为

.
如果使用欧氏距离，则容易定义

.
在每次采样中

离散的遍历区间

,
得到该种采样下的最大距离

.
弗雷歇距离就是使该最大距离最小化的采样方式下的值。
易于理解的，在离散方式下，我们不可能得到真实的弗雷歇距离，而可以无限的趋近。但是越精确的值需要越大的计算量。


基于该离散思想，对应的两条空间(3D)路径弗雷歇距离matlab代码如下：

%% Frechet Distance between two curves (3D)

%%

function f = frechet3D(P1,P2,varargin)

X1=P1(:,1);

X2=P2(:,1);

Y1=P1(:,2);

Y2=P2(:,2);

Z1=P1(:,3);

Z2=P2(:,3);

%get path point length

L1=length(X1);

L2=length(X2);

%check vector lengths

if or(L1~=length(Y1),L2~=length(Y2))

error('Paired input vectors (Xi,Yi) must be the same length.')

end

%check for column inputs

if or(or(size(X1,1)<=1,size(Y1,1)<=1),or(size(X2,1)<=1,size(Y2,1)<=1))

error('Input vectors must be column vectors.')

end

%create maxtrix forms

X1_mat=ones(L2,1)*X1';

Y1_mat=ones(L2,1)*Y1';

Z1_mat=ones(L2,1)*Z1';

X2_mat=X2*ones(1,L1);

Y2_mat=Y2*ones(1,L1);

Z2_mat=Z2*ones(1,L1);

%calculate frechet distance matrix

frechet1=sqrt((X1_mat-X2_mat).^2+(Y1_mat-Y2_mat).^2+(Z1_mat-Z2_mat).^2);

fmin=min(frechet1(:));

fmax=max(frechet1(:));

%handle resolution

if ~isempty(varargin)

res=varargin{1};

if res<=0

error('The resolution parameter must be greater than zero.')

elseif ((fmax-fmin)/res)>10000

warning('Given these two curves, and that resolution, this might take a while.')

elseif res>=(fmax-fmin)

warning('The resolution is too low given these curves to compute anything meaningful.')

f=fmax;

return

end

else

res=(fmax-fmin)/100;

end

%compute frechet distance

clear f

for q3=fmin:res:fmax

im1=bwlabel(frechet1<=q3);

%get region number of beginning and end points

if and(im1(1,1)~=0,im1(1,1)==im1(end,end))

f=q3;

break

end

end

if (~(exist ('f')))

f=fmax;

end

% disp(f)

return

--------
[1] Fréchet, M. Maurice. "Sur quelques points du calcul fonctionnel." Rendiconti del Circolo Matematico di Palermo (1884-1940) 22.1 (1906): 1-72.