中国剩余定理
2017-08-26 13:34
155 查看
Biorhythms
Description
Some people believe that there are three cycles in a person's life that start the day he or she is born. These three cycles are the physical, emotional, and intellectual cycles, and they have periods of lengths 23, 28, and 33 days, respectively. There is one
peak in each period of a cycle. At the peak of a cycle, a person performs at his or her best in the corresponding field (physical, emotional or mental). For example, if it is the mental curve, thought processes will be sharper and concentration will be easier.
Since the three cycles have different periods, the peaks of the three cycles generally occur at different times. We would like to determine when a triple peak occurs (the peaks of all three cycles occur in the same day) for any person. For each cycle, you will
be given the number of days from the beginning of the current year at which one of its peaks (not necessarily the first) occurs. You will also be given a date expressed as the number of days from the beginning of the current year. You task is to determine
the number of days from the given date to the next triple peak. The given date is not counted. For example, if the given date is 10 and the next triple peak occurs on day 12, the answer is 2, not 3. If a triple peak occurs on the given date, you should give
the number of days to the next occurrence of a triple peak.
Input
You will be given a number of cases. The input for each case consists of one line of four integers p, e, i, and d. The values p, e, and i are the number of days from the beginning of the current year at which the physical, emotional, and intellectual cycles
peak, respectively. The value d is the given date and may be smaller than any of p, e, or i. All values are non-negative and at most 365, and you may assume that a triple peak will occur within 21252 days of the given date. The end of input is indicated by
a line in which p = e = i = d = -1.
Output
For each test case, print the case number followed by a message indicating the number of days to the next triple peak, in the form:
Case 1: the next triple peak occurs in 1234 days.
Use the plural form ``days'' even if the answer is 1.
Sample Input
Sample Output
题意:
人自出生起就有体力,情感和智力三个生理周期,分别为23,28和33天
一个周期内有一天为峰值,在这一天,人在对应的方面(体力,情感或智力)表现最好
通常这三个周期的峰值不会是同一天。现在给出三个日期,分别对应于体力,情感,智力出现峰值的日期
然后再给出一个起始日期,要求从这一天开始,算出最少再过多少天后三个峰值同时出现
题解:使用中国剩余定理
[b](互质的模线性方程组)
[/b]
中国剩余定理(CRT)的表述如下
设正整数
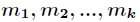
两两互素,则同余方程组

有整数解。并且在模
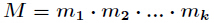
下的解是唯一的,解为

其中
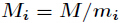
,而
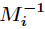
为
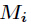
模
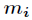
的逆元。
逆元概念:
群G中任意一个元素a,都在G中有唯一的逆元a‘,具有性质aa'=a'a=e,其中e为群的单位元
例如:4关于1模7的乘法逆元为多少?
4X≡1 mod 7
这个方程等价于求一个X和K,满足
4X=7K+1
其中X和K都是整数。
若ax≡1 mod f, 则称a关于模f的乘法逆元为x。也可表示为ax≡1(mod f)。
当a与f互素时,a关于模f的乘法逆元有解。如果不互素,则无解。如果f为素数,则从1到f-1的任意数都与f互素,即在1到f-1之间都恰好有一个关于模f的乘法逆元。
例如,求5关于模14的乘法逆元:
14=5*2+4
5=4*1+1
说明5与14互素,存在5关于14的乘法逆元。
1=5-4=5-(14-5*2)=5*3-14
因此,5关于模14的乘法逆元为3。
其求法可用欧几里得算法,可以见我的另外一片blog,详细推导扩展欧几里得算法
http://blog.csdn.net/summer__show_/article/details/52238225
Extended Euclid (d,f) //算法求d关于模f的乘法逆元d-1 ,即 d* d-1 mod
f = 1
[cpp] view
plain copy
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
void ex_gcd(int a1,int b,int &x,int &y)
{
if(b==0){
x=1,y=0;
return ;
}
ex_gcd(b,a1%b,x,y);
int temp=x;
x=y;
y=temp-(a1/b)*y;
}
int CRT(int a[],int m[],int n)
{
int M=1,ans=0;
for(int i=0;i<n;i++)
M*=m[i];
for(int i=0;i<n;i++){
int x,y;
int Mi =M/m[i];
ex_gcd(Mi,m[i],x,y);
ans=(ans+a[i]*x*Mi)%M;
}
while(ans<0)
ans+=M;
return ans;
}
int main()
{
int d,cnt=1;
int a[10],m[10];
//freopen("in.txt","r",stdin);
while(scanf("%d%d%d%d",&a[0],&a[1],&a[2],&d)!=EOF)
{
if(a[0]==-1&&a[1]==-1&&a[2]==-1&&d==-1)
break;
m[0]=23;
m[1]=28;
m[2]=33;
int ans=CRT(a,m,3);
while(ans<=d)
ans+=21252;
ans-=d;
printf("Case %d: the next triple peak occurs in %d days.\n",cnt++,ans);
}
return 0;
}
下面是中国剩余定理的特殊情况:
不互质的模线性方程组
Strange Way to Express Integers
Description
Elina is reading a book written by Rujia Liu, which introduces a strange way to express non-negative integers. The way is described as following:
Choose k different positive integers a1, a2, …, ak. For some non-negative m, divide it by every ai (1 ≤ i ≤ k) to find
the remainder ri. If a1, a2, …, ak are properly chosen, m can be determined, then the pairs (ai, ri) can be used to express m.
“It is easy to calculate the pairs from m, ” said Elina. “But how can I find m from the pairs?”
Since Elina is new to programming, this problem is too difficult for her. Can you help her?
Input
The input contains multiple test cases. Each test cases consists of some lines.
Line 1: Contains the integer k.
Lines 2 ~ k + 1: Each contains a pair of integers ai, ri (1 ≤ i ≤ k).
Output
Output the non-negative integer m on a separate line for each test case. If there are multiple possible values, output the smallest one. If there are no possible values, output -1.
Sample Input
Sample Output
Hint
All integers in the input and the output are non-negative and can be represented by 64-bit integral types.
题意:
就是给你n组数据
每一组数据a,b 表示 x%a==b
求这n组数据的公共的最小x的解
题解:
中国剩余定理中的不互质的模线性方程组
由不互质的模线性方程组
x%r1=a1 1
x%r2=a2 2
x%r3=a3 3
x%r4=a4 4
......
由 1 2式子得到:
x = r1*k1 + a1
x = r2*k2 + a2
联立:
r1*k1 + a1 =r2*k2 + a2
得到
r1*k1 + r2*k2 = a2 - a1 (其中k2的正负可变)
令g=gcd(r1,r2)
那么上叙方程同时除以g后
r1*k1 / g + r2*k2 / g = (a2 - a1 )/ g
由扩展欧几里得可以得到k1,则有
x1 = r1*k1 + a1 5
x1表示1 2式子得到的r1 和 让r2的最大公约数
(扩展欧几里得算法详解http://blog.csdn.NET/summer__show_/article/details/52238225)
因此1 2式子可以合并成
x = t*lcm(r1,r2) + x1
此时 x 是r1 r2 的最小公倍数,可以返回去验证一下即可
在程序中把5式子变成x = r1*k1 + a1
即 k1=t r1=gcd(r1,r2) a1=x1
然后一直循环求解下去
[cpp] view
plain copy
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
#define LL long long
LL ex_gcd(LL a,LL b,LL &x,LL &y)
{
if(b==0){
x=1,y=0;
return a;
}
LL d=ex_gcd(b,a%b,x,y);
LL temp=x;
x=y;
y=temp-(a/b)*y;
return d;
}
int main()
{
LL k,a1,a2,r1,r2;
LL x,y,d;
// freopen("in.txt","r",stdin);
while(scanf("%I64d",&k)!=EOF)
{
scanf("%I64d%I64d",&a1,&r1);
k--;
int flag=0;
while(k--)
{
scanf("%I64d%I64d",&a2,&r2);
if(flag)
continue;
//扩展欧几里得
LL a=a1,b=a2;
LL c=r2-r1;
d=ex_gcd(a,b,x,y);//最小公约数
if(c%d){
flag=1;
continue;
}
LL t=b/d;//除以d表示方程两边都除以d
x=(x*(c/d)%t+t)%t;
r1=a1*x+r1;//同上面所说的式子5
a1=a1*(a2/d);//a1 a2最大公倍数
}
if(flag)
printf("-1\n");
else
printf("%I64d\n",r1);
}
return 0;
}
Biorhythms
Description
Some people believe that there are three cycles in a person's life that start the day he or she is born. These three cycles are the physical, emotional, and intellectual cycles, and they have periods of lengths 23, 28, and 33 days, respectively. There is one
peak in each period of a cycle. At the peak of a cycle, a person performs at his or her best in the corresponding field (physical, emotional or mental). For example, if it is the mental curve, thought processes will be sharper and concentration will be easier.
Since the three cycles have different periods, the peaks of the three cycles generally occur at different times. We would like to determine when a triple peak occurs (the peaks of all three cycles occur in the same day) for any person. For each cycle, you will
be given the number of days from the beginning of the current year at which one of its peaks (not necessarily the first) occurs. You will also be given a date expressed as the number of days from the beginning of the current year. You task is to determine
the number of days from the given date to the next triple peak. The given date is not counted. For example, if the given date is 10 and the next triple peak occurs on day 12, the answer is 2, not 3. If a triple peak occurs on the given date, you should give
the number of days to the next occurrence of a triple peak.
Input
You will be given a number of cases. The input for each case consists of one line of four integers p, e, i, and d. The values p, e, and i are the number of days from the beginning of the current year at which the physical, emotional, and intellectual cycles
peak, respectively. The value d is the given date and may be smaller than any of p, e, or i. All values are non-negative and at most 365, and you may assume that a triple peak will occur within 21252 days of the given date. The end of input is indicated by
a line in which p = e = i = d = -1.
Output
For each test case, print the case number followed by a message indicating the number of days to the next triple peak, in the form:
Case 1: the next triple peak occurs in 1234 days.
Use the plural form ``days'' even if the answer is 1.
Sample Input
Sample Output
题意:
人自出生起就有体力,情感和智力三个生理周期,分别为23,28和33天
一个周期内有一天为峰值,在这一天,人在对应的方面(体力,情感或智力)表现最好
通常这三个周期的峰值不会是同一天。现在给出三个日期,分别对应于体力,情感,智力出现峰值的日期
然后再给出一个起始日期,要求从这一天开始,算出最少再过多少天后三个峰值同时出现
题解:使用中国剩余定理
[b](互质的模线性方程组)
[/b]
中国剩余定理(CRT)的表述如下
设正整数
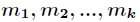
两两互素,则同余方程组

有整数解。并且在模
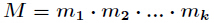
下的解是唯一的,解为

其中
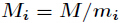
,而
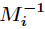
为
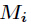
模
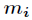
的逆元。
逆元概念:
群G中任意一个元素a,都在G中有唯一的逆元a‘,具有性质aa'=a'a=e,其中e为群的单位元
例如:4关于1模7的乘法逆元为多少?
4X≡1 mod 7
这个方程等价于求一个X和K,满足
4X=7K+1
其中X和K都是整数。
若ax≡1 mod f, 则称a关于模f的乘法逆元为x。也可表示为ax≡1(mod f)。
当a与f互素时,a关于模f的乘法逆元有解。如果不互素,则无解。如果f为素数,则从1到f-1的任意数都与f互素,即在1到f-1之间都恰好有一个关于模f的乘法逆元。
例如,求5关于模14的乘法逆元:
14=5*2+4
5=4*1+1
说明5与14互素,存在5关于14的乘法逆元。
1=5-4=5-(14-5*2)=5*3-14
因此,5关于模14的乘法逆元为3。
其求法可用欧几里得算法,可以见我的另外一片blog,详细推导扩展欧几里得算法
http://blog.csdn.net/summer__show_/article/details/52238225
Extended Euclid (d,f) //算法求d关于模f的乘法逆元d-1 ,即 d* d-1 mod
f = 1
[cpp] view
plain copy
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
void ex_gcd(int a1,int b,int &x,int &y)
{
if(b==0){
x=1,y=0;
return ;
}
ex_gcd(b,a1%b,x,y);
int temp=x;
x=y;
y=temp-(a1/b)*y;
}
int CRT(int a[],int m[],int n)
{
int M=1,ans=0;
for(int i=0;i<n;i++)
M*=m[i];
for(int i=0;i<n;i++){
int x,y;
int Mi =M/m[i];
ex_gcd(Mi,m[i],x,y);
ans=(ans+a[i]*x*Mi)%M;
}
while(ans<0)
ans+=M;
return ans;
}
int main()
{
int d,cnt=1;
int a[10],m[10];
//freopen("in.txt","r",stdin);
while(scanf("%d%d%d%d",&a[0],&a[1],&a[2],&d)!=EOF)
{
if(a[0]==-1&&a[1]==-1&&a[2]==-1&&d==-1)
break;
m[0]=23;
m[1]=28;
m[2]=33;
int ans=CRT(a,m,3);
while(ans<=d)
ans+=21252;
ans-=d;
printf("Case %d: the next triple peak occurs in %d days.\n",cnt++,ans);
}
return 0;
}
下面是中国剩余定理的特殊情况:
不互质的模线性方程组
Strange Way to Express Integers
Description
Elina is reading a book written by Rujia Liu, which introduces a strange way to express non-negative integers. The way is described as following:
Choose k different positive integers a1, a2, …, ak. For some non-negative m, divide it by every ai (1 ≤ i ≤ k) to find
the remainder ri. If a1, a2, …, ak are properly chosen, m can be determined, then the pairs (ai, ri) can be used to express m.
“It is easy to calculate the pairs from m, ” said Elina. “But how can I find m from the pairs?”
Since Elina is new to programming, this problem is too difficult for her. Can you help her?
Input
The input contains multiple test cases. Each test cases consists of some lines.
Line 1: Contains the integer k.
Lines 2 ~ k + 1: Each contains a pair of integers ai, ri (1 ≤ i ≤ k).
Output
Output the non-negative integer m on a separate line for each test case. If there are multiple possible values, output the smallest one. If there are no possible values, output -1.
Sample Input
Sample Output
Hint
All integers in the input and the output are non-negative and can be represented by 64-bit integral types.
题意:
就是给你n组数据
每一组数据a,b 表示 x%a==b
求这n组数据的公共的最小x的解
题解:
中国剩余定理中的不互质的模线性方程组
由不互质的模线性方程组
x%r1=a1 1
x%r2=a2 2
x%r3=a3 3
x%r4=a4 4
......
由 1 2式子得到:
x = r1*k1 + a1
x = r2*k2 + a2
联立:
r1*k1 + a1 =r2*k2 + a2
得到
r1*k1 + r2*k2 = a2 - a1 (其中k2的正负可变)
令g=gcd(r1,r2)
那么上叙方程同时除以g后
r1*k1 / g + r2*k2 / g = (a2 - a1 )/ g
由扩展欧几里得可以得到k1,则有
x1 = r1*k1 + a1 5
x1表示1 2式子得到的r1 和 让r2的最大公约数
(扩展欧几里得算法详解http://blog.csdn.NET/summer__show_/article/details/52238225)
因此1 2式子可以合并成
x = t*lcm(r1,r2) + x1
此时 x 是r1 r2 的最小公倍数,可以返回去验证一下即可
在程序中把5式子变成x = r1*k1 + a1
即 k1=t r1=gcd(r1,r2) a1=x1
然后一直循环求解下去
[cpp] view
plain copy
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
#define LL long long
LL ex_gcd(LL a,LL b,LL &x,LL &y)
{
if(b==0){
x=1,y=0;
return a;
}
LL d=ex_gcd(b,a%b,x,y);
LL temp=x;
x=y;
y=temp-(a/b)*y;
return d;
}
int main()
{
LL k,a1,a2,r1,r2;
LL x,y,d;
// freopen("in.txt","r",stdin);
while(scanf("%I64d",&k)!=EOF)
{
scanf("%I64d%I64d",&a1,&r1);
k--;
int flag=0;
while(k--)
{
scanf("%I64d%I64d",&a2,&r2);
if(flag)
continue;
//扩展欧几里得
LL a=a1,b=a2;
LL c=r2-r1;
d=ex_gcd(a,b,x,y);//最小公约数
if(c%d){
flag=1;
continue;
}
LL t=b/d;//除以d表示方程两边都除以d
x=(x*(c/d)%t+t)%t;
r1=a1*x+r1;//同上面所说的式子5
a1=a1*(a2/d);//a1 a2最大公倍数
}
if(flag)
printf("-1\n");
else
printf("%I64d\n",r1);
}
return 0;
}
转载自:http://blog.csdn.net/summer__show_/article/details/52247673
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 129686 | Accepted: 41277 |
Some people believe that there are three cycles in a person's life that start the day he or she is born. These three cycles are the physical, emotional, and intellectual cycles, and they have periods of lengths 23, 28, and 33 days, respectively. There is one
peak in each period of a cycle. At the peak of a cycle, a person performs at his or her best in the corresponding field (physical, emotional or mental). For example, if it is the mental curve, thought processes will be sharper and concentration will be easier.
Since the three cycles have different periods, the peaks of the three cycles generally occur at different times. We would like to determine when a triple peak occurs (the peaks of all three cycles occur in the same day) for any person. For each cycle, you will
be given the number of days from the beginning of the current year at which one of its peaks (not necessarily the first) occurs. You will also be given a date expressed as the number of days from the beginning of the current year. You task is to determine
the number of days from the given date to the next triple peak. The given date is not counted. For example, if the given date is 10 and the next triple peak occurs on day 12, the answer is 2, not 3. If a triple peak occurs on the given date, you should give
the number of days to the next occurrence of a triple peak.
Input
You will be given a number of cases. The input for each case consists of one line of four integers p, e, i, and d. The values p, e, and i are the number of days from the beginning of the current year at which the physical, emotional, and intellectual cycles
peak, respectively. The value d is the given date and may be smaller than any of p, e, or i. All values are non-negative and at most 365, and you may assume that a triple peak will occur within 21252 days of the given date. The end of input is indicated by
a line in which p = e = i = d = -1.
Output
For each test case, print the case number followed by a message indicating the number of days to the next triple peak, in the form:
Case 1: the next triple peak occurs in 1234 days.
Use the plural form ``days'' even if the answer is 1.
Sample Input
0 0 0 0 0 0 0 100 5 20 34 325 4 5 6 7 283 102 23 320 203 301 203 40 -1 -1 -1 -1
Sample Output
Case 1: the next triple peak occurs in 21252 days. Case 2: the next triple peak occurs in 21152 days. Case 3: the next triple peak occurs in 19575 days. Case 4: the next triple peak occurs in 16994 days. Case 5: the next triple peak occurs in 8910 days. Case 6: the next triple peak occurs in 10789 days.
题意:
人自出生起就有体力,情感和智力三个生理周期,分别为23,28和33天
一个周期内有一天为峰值,在这一天,人在对应的方面(体力,情感或智力)表现最好
通常这三个周期的峰值不会是同一天。现在给出三个日期,分别对应于体力,情感,智力出现峰值的日期
然后再给出一个起始日期,要求从这一天开始,算出最少再过多少天后三个峰值同时出现
题解:使用中国剩余定理
[b](互质的模线性方程组)
[/b]
中国剩余定理(CRT)的表述如下
设正整数
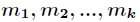
两两互素,则同余方程组

有整数解。并且在模
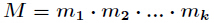
下的解是唯一的,解为

其中
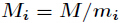
,而
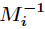
为
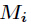
模
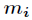
的逆元。
逆元概念:
群G中任意一个元素a,都在G中有唯一的逆元a‘,具有性质aa'=a'a=e,其中e为群的单位元
例如:4关于1模7的乘法逆元为多少?
4X≡1 mod 7
这个方程等价于求一个X和K,满足
4X=7K+1
其中X和K都是整数。
若ax≡1 mod f, 则称a关于模f的乘法逆元为x。也可表示为ax≡1(mod f)。
当a与f互素时,a关于模f的乘法逆元有解。如果不互素,则无解。如果f为素数,则从1到f-1的任意数都与f互素,即在1到f-1之间都恰好有一个关于模f的乘法逆元。
例如,求5关于模14的乘法逆元:
14=5*2+4
5=4*1+1
说明5与14互素,存在5关于14的乘法逆元。
1=5-4=5-(14-5*2)=5*3-14
因此,5关于模14的乘法逆元为3。
其求法可用欧几里得算法,可以见我的另外一片blog,详细推导扩展欧几里得算法
http://blog.csdn.net/summer__show_/article/details/52238225
Extended Euclid (d,f) //算法求d关于模f的乘法逆元d-1 ,即 d* d-1 mod
f = 1
[cpp] view
plain copy
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
void ex_gcd(int a1,int b,int &x,int &y)
{
if(b==0){
x=1,y=0;
return ;
}
ex_gcd(b,a1%b,x,y);
int temp=x;
x=y;
y=temp-(a1/b)*y;
}
int CRT(int a[],int m[],int n)
{
int M=1,ans=0;
for(int i=0;i<n;i++)
M*=m[i];
for(int i=0;i<n;i++){
int x,y;
int Mi =M/m[i];
ex_gcd(Mi,m[i],x,y);
ans=(ans+a[i]*x*Mi)%M;
}
while(ans<0)
ans+=M;
return ans;
}
int main()
{
int d,cnt=1;
int a[10],m[10];
//freopen("in.txt","r",stdin);
while(scanf("%d%d%d%d",&a[0],&a[1],&a[2],&d)!=EOF)
{
if(a[0]==-1&&a[1]==-1&&a[2]==-1&&d==-1)
break;
m[0]=23;
m[1]=28;
m[2]=33;
int ans=CRT(a,m,3);
while(ans<=d)
ans+=21252;
ans-=d;
printf("Case %d: the next triple peak occurs in %d days.\n",cnt++,ans);
}
return 0;
}
下面是中国剩余定理的特殊情况:
不互质的模线性方程组
Strange Way to Express Integers
| Time Limit: 1000MS | Memory Limit: 131072K | |
| Total Submissions: 14111 | Accepted: 4564 |
Elina is reading a book written by Rujia Liu, which introduces a strange way to express non-negative integers. The way is described as following:
Choose k different positive integers a1, a2, …, ak. For some non-negative m, divide it by every ai (1 ≤ i ≤ k) to find
the remainder ri. If a1, a2, …, ak are properly chosen, m can be determined, then the pairs (ai, ri) can be used to express m.
“It is easy to calculate the pairs from m, ” said Elina. “But how can I find m from the pairs?”
Since Elina is new to programming, this problem is too difficult for her. Can you help her?
Input
The input contains multiple test cases. Each test cases consists of some lines.
Line 1: Contains the integer k.
Lines 2 ~ k + 1: Each contains a pair of integers ai, ri (1 ≤ i ≤ k).
Output
Output the non-negative integer m on a separate line for each test case. If there are multiple possible values, output the smallest one. If there are no possible values, output -1.
Sample Input
2 8 7 11 9
Sample Output
31
Hint
All integers in the input and the output are non-negative and can be represented by 64-bit integral types.
题意:
就是给你n组数据
每一组数据a,b 表示 x%a==b
求这n组数据的公共的最小x的解
题解:
中国剩余定理中的不互质的模线性方程组
由不互质的模线性方程组
x%r1=a1 1
x%r2=a2 2
x%r3=a3 3
x%r4=a4 4
......
由 1 2式子得到:
x = r1*k1 + a1
x = r2*k2 + a2
联立:
r1*k1 + a1 =r2*k2 + a2
得到
r1*k1 + r2*k2 = a2 - a1 (其中k2的正负可变)
令g=gcd(r1,r2)
那么上叙方程同时除以g后
r1*k1 / g + r2*k2 / g = (a2 - a1 )/ g
由扩展欧几里得可以得到k1,则有
x1 = r1*k1 + a1 5
x1表示1 2式子得到的r1 和 让r2的最大公约数
(扩展欧几里得算法详解http://blog.csdn.NET/summer__show_/article/details/52238225)
因此1 2式子可以合并成
x = t*lcm(r1,r2) + x1
此时 x 是r1 r2 的最小公倍数,可以返回去验证一下即可
在程序中把5式子变成x = r1*k1 + a1
即 k1=t r1=gcd(r1,r2) a1=x1
然后一直循环求解下去
[cpp] view
plain copy
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
#define LL long long
LL ex_gcd(LL a,LL b,LL &x,LL &y)
{
if(b==0){
x=1,y=0;
return a;
}
LL d=ex_gcd(b,a%b,x,y);
LL temp=x;
x=y;
y=temp-(a/b)*y;
return d;
}
int main()
{
LL k,a1,a2,r1,r2;
LL x,y,d;
// freopen("in.txt","r",stdin);
while(scanf("%I64d",&k)!=EOF)
{
scanf("%I64d%I64d",&a1,&r1);
k--;
int flag=0;
while(k--)
{
scanf("%I64d%I64d",&a2,&r2);
if(flag)
continue;
//扩展欧几里得
LL a=a1,b=a2;
LL c=r2-r1;
d=ex_gcd(a,b,x,y);//最小公约数
if(c%d){
flag=1;
continue;
}
LL t=b/d;//除以d表示方程两边都除以d
x=(x*(c/d)%t+t)%t;
r1=a1*x+r1;//同上面所说的式子5
a1=a1*(a2/d);//a1 a2最大公倍数
}
if(flag)
printf("-1\n");
else
printf("%I64d\n",r1);
}
return 0;
}
Biorhythms
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 129686 | Accepted: 41277 |
Some people believe that there are three cycles in a person's life that start the day he or she is born. These three cycles are the physical, emotional, and intellectual cycles, and they have periods of lengths 23, 28, and 33 days, respectively. There is one
peak in each period of a cycle. At the peak of a cycle, a person performs at his or her best in the corresponding field (physical, emotional or mental). For example, if it is the mental curve, thought processes will be sharper and concentration will be easier.
Since the three cycles have different periods, the peaks of the three cycles generally occur at different times. We would like to determine when a triple peak occurs (the peaks of all three cycles occur in the same day) for any person. For each cycle, you will
be given the number of days from the beginning of the current year at which one of its peaks (not necessarily the first) occurs. You will also be given a date expressed as the number of days from the beginning of the current year. You task is to determine
the number of days from the given date to the next triple peak. The given date is not counted. For example, if the given date is 10 and the next triple peak occurs on day 12, the answer is 2, not 3. If a triple peak occurs on the given date, you should give
the number of days to the next occurrence of a triple peak.
Input
You will be given a number of cases. The input for each case consists of one line of four integers p, e, i, and d. The values p, e, and i are the number of days from the beginning of the current year at which the physical, emotional, and intellectual cycles
peak, respectively. The value d is the given date and may be smaller than any of p, e, or i. All values are non-negative and at most 365, and you may assume that a triple peak will occur within 21252 days of the given date. The end of input is indicated by
a line in which p = e = i = d = -1.
Output
For each test case, print the case number followed by a message indicating the number of days to the next triple peak, in the form:
Case 1: the next triple peak occurs in 1234 days.
Use the plural form ``days'' even if the answer is 1.
Sample Input
0 0 0 0 0 0 0 100 5 20 34 325 4 5 6 7 283 102 23 320 203 301 203 40 -1 -1 -1 -1
Sample Output
Case 1: the next triple peak occurs in 21252 days. Case 2: the next triple peak occurs in 21152 days. Case 3: the next triple peak occurs in 19575 days. Case 4: the next triple peak occurs in 16994 days. Case 5: the next triple peak occurs in 8910 days. Case 6: the next triple peak occurs in 10789 days.
题意:
人自出生起就有体力,情感和智力三个生理周期,分别为23,28和33天
一个周期内有一天为峰值,在这一天,人在对应的方面(体力,情感或智力)表现最好
通常这三个周期的峰值不会是同一天。现在给出三个日期,分别对应于体力,情感,智力出现峰值的日期
然后再给出一个起始日期,要求从这一天开始,算出最少再过多少天后三个峰值同时出现
题解:使用中国剩余定理
[b](互质的模线性方程组)
[/b]
中国剩余定理(CRT)的表述如下
设正整数
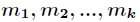
两两互素,则同余方程组

有整数解。并且在模
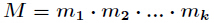
下的解是唯一的,解为

其中
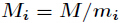
,而
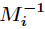
为
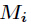
模
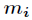
的逆元。
逆元概念:
群G中任意一个元素a,都在G中有唯一的逆元a‘,具有性质aa'=a'a=e,其中e为群的单位元
例如:4关于1模7的乘法逆元为多少?
4X≡1 mod 7
这个方程等价于求一个X和K,满足
4X=7K+1
其中X和K都是整数。
若ax≡1 mod f, 则称a关于模f的乘法逆元为x。也可表示为ax≡1(mod f)。
当a与f互素时,a关于模f的乘法逆元有解。如果不互素,则无解。如果f为素数,则从1到f-1的任意数都与f互素,即在1到f-1之间都恰好有一个关于模f的乘法逆元。
例如,求5关于模14的乘法逆元:
14=5*2+4
5=4*1+1
说明5与14互素,存在5关于14的乘法逆元。
1=5-4=5-(14-5*2)=5*3-14
因此,5关于模14的乘法逆元为3。
其求法可用欧几里得算法,可以见我的另外一片blog,详细推导扩展欧几里得算法
http://blog.csdn.net/summer__show_/article/details/52238225
Extended Euclid (d,f) //算法求d关于模f的乘法逆元d-1 ,即 d* d-1 mod
f = 1
[cpp] view
plain copy
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
void ex_gcd(int a1,int b,int &x,int &y)
{
if(b==0){
x=1,y=0;
return ;
}
ex_gcd(b,a1%b,x,y);
int temp=x;
x=y;
y=temp-(a1/b)*y;
}
int CRT(int a[],int m[],int n)
{
int M=1,ans=0;
for(int i=0;i<n;i++)
M*=m[i];
for(int i=0;i<n;i++){
int x,y;
int Mi =M/m[i];
ex_gcd(Mi,m[i],x,y);
ans=(ans+a[i]*x*Mi)%M;
}
while(ans<0)
ans+=M;
return ans;
}
int main()
{
int d,cnt=1;
int a[10],m[10];
//freopen("in.txt","r",stdin);
while(scanf("%d%d%d%d",&a[0],&a[1],&a[2],&d)!=EOF)
{
if(a[0]==-1&&a[1]==-1&&a[2]==-1&&d==-1)
break;
m[0]=23;
m[1]=28;
m[2]=33;
int ans=CRT(a,m,3);
while(ans<=d)
ans+=21252;
ans-=d;
printf("Case %d: the next triple peak occurs in %d days.\n",cnt++,ans);
}
return 0;
}
下面是中国剩余定理的特殊情况:
不互质的模线性方程组
Strange Way to Express Integers
| Time Limit: 1000MS | Memory Limit: 131072K | |
| Total Submissions: 14111 | Accepted: 4564 |
Elina is reading a book written by Rujia Liu, which introduces a strange way to express non-negative integers. The way is described as following:
Choose k different positive integers a1, a2, …, ak. For some non-negative m, divide it by every ai (1 ≤ i ≤ k) to find
the remainder ri. If a1, a2, …, ak are properly chosen, m can be determined, then the pairs (ai, ri) can be used to express m.
“It is easy to calculate the pairs from m, ” said Elina. “But how can I find m from the pairs?”
Since Elina is new to programming, this problem is too difficult for her. Can you help her?
Input
The input contains multiple test cases. Each test cases consists of some lines.
Line 1: Contains the integer k.
Lines 2 ~ k + 1: Each contains a pair of integers ai, ri (1 ≤ i ≤ k).
Output
Output the non-negative integer m on a separate line for each test case. If there are multiple possible values, output the smallest one. If there are no possible values, output -1.
Sample Input
2 8 7 11 9
Sample Output
31
Hint
All integers in the input and the output are non-negative and can be represented by 64-bit integral types.
题意:
就是给你n组数据
每一组数据a,b 表示 x%a==b
求这n组数据的公共的最小x的解
题解:
中国剩余定理中的不互质的模线性方程组
由不互质的模线性方程组
x%r1=a1 1
x%r2=a2 2
x%r3=a3 3
x%r4=a4 4
......
由 1 2式子得到:
x = r1*k1 + a1
x = r2*k2 + a2
联立:
r1*k1 + a1 =r2*k2 + a2
得到
r1*k1 + r2*k2 = a2 - a1 (其中k2的正负可变)
令g=gcd(r1,r2)
那么上叙方程同时除以g后
r1*k1 / g + r2*k2 / g = (a2 - a1 )/ g
由扩展欧几里得可以得到k1,则有
x1 = r1*k1 + a1 5
x1表示1 2式子得到的r1 和 让r2的最大公约数
(扩展欧几里得算法详解http://blog.csdn.NET/summer__show_/article/details/52238225)
因此1 2式子可以合并成
x = t*lcm(r1,r2) + x1
此时 x 是r1 r2 的最小公倍数,可以返回去验证一下即可
在程序中把5式子变成x = r1*k1 + a1
即 k1=t r1=gcd(r1,r2) a1=x1
然后一直循环求解下去
[cpp] view
plain copy
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
#define LL long long
LL ex_gcd(LL a,LL b,LL &x,LL &y)
{
if(b==0){
x=1,y=0;
return a;
}
LL d=ex_gcd(b,a%b,x,y);
LL temp=x;
x=y;
y=temp-(a/b)*y;
return d;
}
int main()
{
LL k,a1,a2,r1,r2;
LL x,y,d;
// freopen("in.txt","r",stdin);
while(scanf("%I64d",&k)!=EOF)
{
scanf("%I64d%I64d",&a1,&r1);
k--;
int flag=0;
while(k--)
{
scanf("%I64d%I64d",&a2,&r2);
if(flag)
continue;
//扩展欧几里得
LL a=a1,b=a2;
LL c=r2-r1;
d=ex_gcd(a,b,x,y);//最小公约数
if(c%d){
flag=1;
continue;
}
LL t=b/d;//除以d表示方程两边都除以d
x=(x*(c/d)%t+t)%t;
r1=a1*x+r1;//同上面所说的式子5
a1=a1*(a2/d);//a1 a2最大公倍数
}
if(flag)
printf("-1\n");
else
printf("%I64d\n",r1);
}
return 0;
}
转载自:http://blog.csdn.net/summer__show_/article/details/52247673
相关文章推荐
- poj 2981 Strange Way to Express Integers (中国剩余定理不互质)
- 中国剩余定理的实现《一》长整型
- 中国剩余定理及其扩展——学习(复习)笔记
- 扩展欧几里得、中国剩余定理 入门指南
- 中国剩余定理
- 5.扩展欧几里得&&中国剩余定理
- HDU 1420 Prepared for New Acmer【中国剩余定理】
- hdu 4878 ZCC loves words AC自动机+中国剩余定理+快速幂
- 中国剩余定理
- HDU1370Biorhythms(中国剩余定理||暴力)
- ACM题 Biorhythms 将中国剩余定理的思想包含在程序中
- 模数非互质的同余方程组(非互质版中国剩余定理)
- 51nod1079 中国剩余定理
- poj 1006 中国剩余定理
- poj 1006 中国剩余定理解同余方程
- 中国剩余定理的学习
- 扩展欧几里德算法 线性同余方程 中国剩余定理
- 中国剩余定理
- 复习数学之中国剩余定理和欧拉定理和扩展欧几里德
- 【中国剩余定理-非互质】POJ2891[Strange Way to Express Integers]题解
