降维--主成分分析（PCA）

1 引言

主成分分析（Principal Component Analysis, PCA）是一种经典又常用的数据降维算法（注意这里的降维是指特征提取 ，有时也称子空间学习，还有一支叫特征选择，有兴趣可参这篇博客），它的主要思想是寻找数据分布方差最大的投影方向，初次听好像也不太好理解，那就上个图瞧瞧咯。



图1

如图1标注出了信号和噪音的方差方向。我们找数据变化大的方向，变化大则含信息量大，所以认为它代表信号方向，而认为小的数据波动是由噪音引起。事实上，有个叫信噪比的指标：SNR=σ2signal/σ2noise，SNR越大(≫1)，说明信息越准确噪音越少。图中用x,y坐标轴来描述这些数据点的位置，如果我们忽略次要因素，抓主要矛盾，就可以用一个沿着信号方向的轴（投影方向），来刻画这些点，虽然可能会损失一些有用的信息，但是这个过程中我们简化了问题，实现了降维：从二维到一维。

小结一下降维大法的好处：降维可以去除数据中的冗余特征，相应也可减少数据存储空间，更重要的是，方便后续各种算法对数据的进一步处理、分析！这一小节到这里本应结束，但我还想再上个酷炫的图，已超出PCA范畴，可跳过不看。



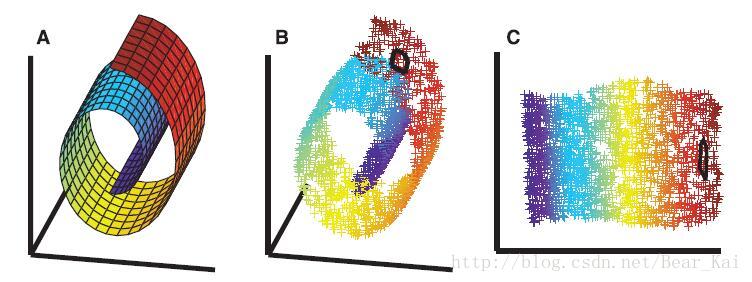
图2

如图2A，把一张“彩色的纸”卷起来。如图2B，在纸上随机选取一些数据。如图2C，把纸摊开。不同的颜色代表不同的类别，在现实生活中，数据的呈现形式往往是这个B样子，不仅需要在更高维的空间中描述它们，而且往往导致数据更难区分（同类数据间的欧式距离甚至比非同类的距离都大），所以最好就是找到简单又好分的数据本质的分布空间如C，这种B到C的降维技术就是传说中的流形学习(manifold learning)，典型代表有LLE，LPP，NPE等，在此按住不提，总之流行学习是关注局部结构，而PCA关注的是全局。

2 目标函数及求解

上一节简要介绍了PCA的思想，提到了PCA就是找方差大的方向，这一节就是解决怎样来找这些方向。在机器学习模型中，常针对一个要求解的问题，提出若干准则，以此提出一个目标函数，再在数学上对目标函数进行优化，得出问题的解。PCA的准则是，让投影后的数据分布方差尽可能大，所以PCA的目标函数可以这样定义：

max1n∑i=1n(yi−y¯)2=maxwTw=11n∑i=1n(wTxi)2=maxwTw=1wT(1nXXT)w=maxwTw=1wTCxw(2.1) 其中，w∈Rd表示投影方向，yi=wTxi是投影后的数据点，X=[x1,…,xn]∈Rd×n是数据矩阵，且我们假设它已经被零均值化处理过，即x¯=1n∑ixi=0，也自然有y¯=0。Cx就是协方差矩阵，有时也用修正后的，即Cx=1n−1XXT。关于正交约束，可以这样简单理解，一个作用是使目标式子有解，限制w的变化范围，另一个作用是选择标准化的坐标轴，接下来会再提到。

上面是学了一个投影方向（也称子空间），即把数据降成一维，如果要学多个投影方向，很自然地，我们可以让它们的和最大，即：

max∀j,wTjwj=1∑j=1cwTjCxwj=maxWTW=IcTr(WTCxW)(2.2) 这里，W=[w1,…,wc]∈Rd×c是投影矩阵，Ic∈Rc×c表示单位矩阵，正交约束使得各投影方向自身是标准化的，且它们之间是两两正交的，为什么要正交，可简单类比我们常用x,y轴表示平面上的点，用xyz轴表示三维空间中的点，都是为了使问题简化而已。

现在就要来求解上述提出的目标式子，更一般地，我们直接对式(2.2)进行操作。设Λ∈Rc×c为拉格朗日乘子，式(2.2)的拉格朗日函数为：

J(W)=Tr(WTCxW)−Tr(Λ(WTW−Ic))(2.3) 求导并置零得：

∂J(W)∂W=2CxW−W(Λ+ΛT)=0(2.4) 记Λ~=12(Λ+ΛT)，有CxW=WΛ~。所以，W就是CX的特征向量矩阵，Λ~是对应的特征值组成的对角矩阵。J(W)=Tr(WTWΛ~)=Tr(Λ~)，要最大化J(W)，自然取Cx的前c个最大的特征值，相应地，W就是由Cx的前c大特征值对应的特征向量按列组成的矩阵。通过投影矩阵W，数据从d维降低到c维。

关于主成分个数(c)，通常根据需要保留的方差百分比，即需要保留的信息量来确定。比如我们要保留99%的信息量，将λ从大到小排列，即λ1>λ2>…>λn，找到最小的k，使满足：

∑kj=1λj∑nj=1λj≥0.99

3 再理解

上一节，我们走完了机器学习中传统的目标引出和公式推导过程，这一节中，我们尝试从另外几个角度来剖析PCA，感受一下殊途同归。

3.1 特征值分解

前面已经引出了协方差的概念，在概率论和统计学中，协方差用于衡量变量之间的总体误差，方差是协方差的特例，即两个变量相同情况下的协方差。在协方差矩阵中，对角线元素对应了各变量自身的方差大小，非对角线元素就是不同变量之间的协方差。如果两个变量是统计独立的，那么两者之间的协方差就是0。（为了避免侧重点跑偏，关于协方差的具体内容在此不做展开，有兴趣可自行谷歌/百度）

所以我们可以直接拿协方差矩阵做文章，简单分析一下，我们想要的协方差矩阵应该是介个样纸的：对角线元素尽可能大，非对角线元素尽量为0，即协方差矩阵最好是一个对角阵。原始数据X，对应原始协方差矩阵Cx，Cx通常含有冗余特征，即非对角，现在我们想要通过一个投影变换Y=WTX，使得降维后新数据的协方差矩阵Cy=WTCxW (近似)为对角阵。注意Cx实对称，是一个正规矩阵(满足ATA=AAT,A∈Rn×n)，根据矩阵论的知识，一定可以对角化：D=PTCxP，其中P∈Rd×d由Cx的特征向量按列组成，且P是个正交阵，D∈Rd×d是对应的特征值组成的对角矩阵。嘿！这不就是我们想要的对角矩阵嘛，对比Cy=WTCxW，我们可令W由P的某c列按列组成，因为我们想要对角元素尽可能大，这c列自然是对应Cx的前c大特征值的列(特征向量)，跟上一节中推导的结果一致！

3.2 奇异值分解(SVD)

SVD(singular value decomposition)，即奇异值分解，跟上一小节的特征值分解有很大关联，我们不妨先来对比一下两者：

方法	表示	说明
特征值分解	A=PΛP−1	A是方阵，P可逆但不需要是正交阵，Λ不需要是半正定阵(因为可以有λ<0)
SVD	A=UΣVT	A不需要为方阵， U,V是正交阵，Σ为半正定阵(因为奇异值≥0)

【注】方阵A半正定：∀x∈Rn,有xTAx≥0

令Y~=1n√XT，则有Y~TY~=1nXXT=Cx。对Y~进行SVD：Y~=UΣVT，那么V就包含了YTY也即Cx的特征向量。SVD这个角度更多地是为了求解的方便(即已知我们要求解的投影方向就是协方差矩阵的特征向量)，在数值计算上，SVD比特征值分解要稳定一些，而且对一个n×n的矩阵进行特征分解的计算复杂度高达O(n3)。

补充：不难发现，对于一个对称半正定矩阵A(保证了可对角化和特征值≥0)，特征分解和奇异值分解是等价的，因为A=PΛPT既可以看做是特征分解，也可以看做是U=V时的奇异值分解，此时A的特征值=奇异值。无巧不成书，幸运的我们幸运地发现，Cx正是这样一个对称半正定阵！所以实际上，我们对Cx进行特征分解或者SVD都是可以得到投影方向滴。

3.3 数据重构

也可从数据重构的角度来看待PCA，主要思想是将投影后的数据重新投影回原空间，使得数据的重构误差最小，公式化表述就是：

minW∈Rd×c∥X−WWTX∥2Fs.t.wTiwj=0(i≠j),wTiwi=1(3.1) 首先，如果我们保留100%的信息量，即选择的主成分个数c就等于原始维度d，相当于不降维，W是d×d大小的正交矩阵，有WWT=Id，此时重构误差为0。下面，我们来证明式(3.1)等价于式(2.2)。

(3.1)⇔minWTW=IcTr(X−WWTX)T(X−WWTX)⇔maxWTW=IcTr(XTWWTX)⇔maxWTW=Ic1nTr(WTXXTW)⇔(2.2) 【注】上面第一个等价就是按定义展开，第二个是去掉了一些无关的常数项，不影响最大或最小问题的解，第三个用到了迹的性质Tr(AB)=Tr(BA)。

3.4 低秩近似

还有一种观点，认为PCA是找一个低秩矩阵来近似数据矩阵，用欧式距离来衡量的话，就是：

minrank(Z)=c∥X−Z∥2F.(3.2) 根据满秩分解，Z∈Rd×n可以分解为：Z=UVT，其中U∈Rd×c,V∈Rn×c，且有UTU=Ic。式(2.2)可以改写为：

minUTU=Ic,V∥X−UVT∥2F.(3.2) 这里，U可以看做是d维空间的c个基，V可以看做是数据点在该空间中的(低维)表达。下面我们还是来把式(3.2)跟式(2.2)联系起来。式(3.2)对V求偏导并置零，可得V=XTU，代回(3.2)中可得：

maxUTU=IcTr(UTXXTU).(3.3) 又回到最初的起点啦，即PCA现在跟低秩近似也联系起来了。

4 拓展

对本节内容如果有兴趣但没时间仔细看过程，大概浏览一下结论就行，这一节主要就是输出一种认识，学习和生活中，不要轻易小瞧看似简单的人/物，觉得自己了然了看穿了，可能只是因为自己还在雾中。

4.1 PCA与Kmeans

PCA是经典的降维算法，Kmeans是经典的聚类算法，在这一小节里，咱们来瞅瞅它们两个在私底下会不会有什么基情。Kmeans大意是先随机给定一些聚类中心，然后依据数据点距聚类中心的远近给数据分配簇标签，然后计算新的聚类中心，然后再重新分配，然后再计算，再分配……最终聚类中心会移动到一个比较好的位置，使得数据点距聚类中心的距离的平方和比较小。对，就是根据距离的平方和作为准则的，所以目标函数自然可以这样写：

minCk∑k=1K∑i∈Ck∥xi−mk∥2(4.1) 这就是我们常见的Kmeans目标式，其中K表示簇的个数，Ck表示第k个簇的数据点集合，mk=∑i∈Ck1nkxi表示第k个簇的聚类中心，nk表示第k个簇中的数据点个数。仅通过(4.1)好像看不出什么名堂，那我们就来变一变，看能不能写出更简便的表达式，因为是要找跟PCA之间的关系，所以联想PCA的目标式，看能不能跟(2.2)套一下近乎。下面是公式推导：

(4.1)⇔min∑k=1K∑i∈Ck(xTixi−2xTimk+mTkmk)⇔min∑i=1nxTixi−2∑k=1K∑i∈CkxTimk+∑k=1KnkmTkmk⇔min∑i=1nxTixi−∑k=1K∑i∈CkxTimk(∵nkmTkmk=∑i∈CkxTimk)⇔min∑i=1nxTixi−∑k=1K1nk∑i,j∈CkxTixj⇔minTr(XTX)−Tr(HTXTXH)⇔maxHTH=I,H≥0Tr(HTKH)(4.2) 其中引入了一个指示(或标签)矩阵H∈Rn×k，如果xi是第j个簇的，则Hij=1/nk−−√，否则为0。比如现在有5个样例分别属于两个簇，前两个属于第一个簇，后三个属于第二个簇，则H长这个样纸： [1/2√01/2√001/3√01/3√01/3√]T K=XTX是相似度矩阵，这里是采用的标准内积线性核，也可以扩展到其它核，在此不做赘述。到这里可以小激动一下，因为式(4.2)相比式(4.1)不仅看起来简明多了，而且看上去跟我们目标式(2.2)长得很像，那式(4.2)的解跟式(2.2)的解怎么联系起来呢？还记得上一节中说的特征值分解和SVD分解吧，我们再把它们拿出来瞧瞧（此处忽略Cx中的1n，且不考虑Cx不可逆的情况）：

X=UΣVTCx=XXT=UΛUTK=XTX=VΛVT 上面U∈Rd×c就是PCA中要求的投影矩阵W，V是式(4.2)松弛非负约束后的指示矩阵H。从第一行中的式子可以知道，V=XTUΣ−1，这说明了什么啊，说明PCA实际上是在进行一种松弛化的Kmeans聚类，簇的指示矩阵就是投影后的数据矩阵(再缩放一下)。

拓展的拓展：1）kernel Kmeans跟谱聚类(spectral clustering)有关系；2）实际上，XXT也叫总体散度矩阵，XHHTXT是类间散度矩阵，可参见线性判别分析LDA，它是另一种经典的降维算法，PCA是无监督的，LDA是有监督。所以Kmeas实际上在minHTr(Sw)，这里Sw=St−Sb是类内散度矩阵。3）LDA是已知标签，调整投影矩阵，Kmeans是调整标签。

4.2 Robust PCA

关于鲁棒PCA这个方向，也有很多研究成果，这里只简单地提一种思路，是关于用ℓ1-norm替代ℓ2-norm的，这是一种在机器学习中内十分常用的手法，用于实现鲁棒性或稀疏性。涉及到范数，我们先把式(2.2)改写一下：

minWTW=Ic1n∑i=1n∥WTxi∥22(4.1) 那么鲁棒PCA就是：

minWTW=Ic1n∑i=1n∥WTxi∥1(4.1) 关于求解的问题超出本文范畴，感兴趣地可以看相关论文。

主要参考文献

【1】Shlens J. A Tutorial on Principal Component Analysis[J]. 2014, 51(3):219-226.

【2】http://ufldl.stanford.edu/tutorial/unsupervised/PCAWhitening/

【3】Ding C H Q, He X. Principal Component Analysis and Effective K-Means Clustering[C]. SIAM ICDM. DBLP, 2004:126–143.

【4】Masaeli M, Yan Y, Cui Y, et al. Convex Principal Feature Selection[C]. SIAM ICDM. DBLP, 2010:619-628.

【5】Nie F, Yuan J, Huang H. Optimal mean robust principal component analysis[C]. ICML. 2014:1062-1070.

【6】Nie F, Huang H, Ding C, et al. Robust Principal Component Analysis with Non-Greedy L1-Norm Maximization[C]. IJCAI. 2011:1433-1438.