MP算法和OMP算法及其思想与实现
2017-01-09 16:29
483 查看
主要介绍MP(Matching Pursuits)算法和OMP(Orthogonal Matching Pursuit)算法[1],这两个算法虽然在90年代初就提出来了,但作为经典的算法,国内文献(可能有我没有搜索到)都仅描述了算法步骤和简单的应用,并未对其进行详尽的分析,国外的文献还是分析的很透彻,所以我结合自己的理解,来分析一下写到博客里,算作笔记。
1. 信号的稀疏表示(sparse representation of signals)
给定一个过完备字典矩阵
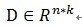
,其中它的每列表示一种原型信号的原子。给定一个信号y,它可以被表示成这些原子的稀疏线性组合。信号 y 可以被表达为 y = Dx ,或者
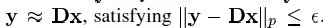
。
字典矩阵中所谓过完备性,指的是原子的个数远远大于信号y的长度(其长度很显然是n),即n<<k。
2.MP算法(匹配追踪算法)
2.1 算法描述
作为对信号进行稀疏分解的方法之一,将信号在完备字典库上进行分解。
假定被表示的信号为y,其长度为n。假定H表示Hilbert空间,在这个空间H里,由一组向量
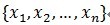
构成字典矩阵D,其中每个向量可以称为原子(atom),其长度与被表示信号 y 的长度n相同,而且这些向量已作为归一化处理,即|
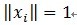
,也就是单位向量长度为1。MP算法的基本思想:从字典矩阵D(也称为过完备原子库中),选择一个与信号
y 最匹配的原子(也就是某列),构建一个稀疏逼近,并求出信号残差,然后继续选择与信号残差最匹配的原子,反复迭代,信号y可以由这些原子来线性和,再加上最后的残差值来表示。很显然,如果残差值在可以忽略的范围内,则信号y就是这些原子的线性组合。如果选择与信号y最匹配的原子?如何构建稀疏逼近并求残差?如何进行迭代?我们来详细介绍使用MP进行信号分解的步骤:[1] 计算信号 y 与字典矩阵中每列(原子)的内积,选择绝对值最大的一个原子,它就是与信号 y 在本次迭代运算中最匹配的。用专业术语来描述:令信号
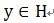
,从字典矩阵中选择一个最为匹配的原子,满足
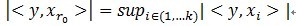
,r0
表示一个字典矩阵的列索引。这样,信号 y 就被分解为在最匹配原子
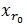
的垂直投影分量和残值两部分,即:
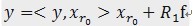
。[2]对残值R1f进行步骤[1]同样的分解,那么第K步可以得到:
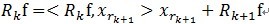
, 其中
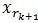
满足
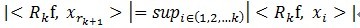
。可见,经过K步分解后,信号
y 被分解为:

,其中
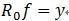
。
2.2 继续讨论
(1)为什么要假定在Hilbert空间中?Hilbert空间就是定义了完备的内积空。很显然,MP中的计算使用向量的内积运算,所以在在Hilbert空间中进行信号分解理所当然了。什么是完备的内积空间?篇幅有限就请自己搜索一下吧。
(2)为什么原子要事先被归一化处理了,即上面的描述
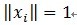
。内积常用于计算一个矢量在一个方向上的投影长度,这时方向的矢量必须是单位矢量。MP中选择最匹配的原子是,是选择内积最大的一个,也就是信号(或是残值)在原子(单位的)垂直投影长度最长的一个,比如第一次分解过程中,投影长度就是
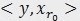
。
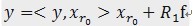
,三个向量,构成一个三角形,且
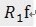
和
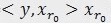
正交(不能说垂直,但是可以想象二维空间这两个矢量是垂直的)。
(3)MP算法是收敛的,因为
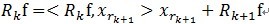
,
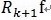
和
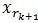
正交,由这两个可以得出
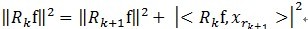
,得出每一个残值比上一次的小,故而收敛。
2.3 MP算法的缺点
如上所述,如果信号(残值)在已选择的原子进行垂直投影是非正交性的,这会使得每次迭代的结果并不少最优的而是次最优的,收敛需要很多次迭代。举个例子说明一下:在二维空间上,有一个信号 y 被 D=[x1, x2]来表达,MP算法迭代会发现总是在x1和x2上反复迭代,即
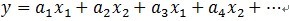
,这个就是信号(残值)在已选择的原子进行垂直投影的非正交性导致的。再用严谨的方式描述[1]可能容易理解:在Hilbert空间H中,
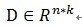
,
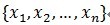
,定义
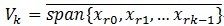
,就是它是这些向量的张成中的一个,MP构造一种表达形式:
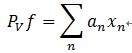
;这里的Pvf表示
f在V上的一个正交投影操作,那么MP算法的第 k 次迭代的结果可以表示如下(前面描述时信号为y,这里变成f了,请注意):
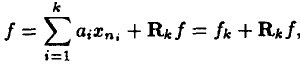
如果

是最优的k项近似值,当且仅当
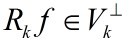
。由于MP仅能保证
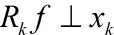
,所以

一般情况下是次优的。这是什么意思呢?

是k个项的线性表示,这个组合的值作为近似值,只有在第k个残差和

正交,才是最优的。如果第k个残值与

正交,意味这个残值与fk的任意一项都线性无关,那么第k个残值在后面的分解过程中,不可能出现fk中已经出现的项,这才是最优的。而一般情况下,不能满足这个条件,MP一般只能满足第k个残差和xk正交,这也就是前面为什么提到“信号(残值)在已选择的原子进行垂直投影是非正交性的”的原因。如果第k个残差和fk不正交,那么后面的迭代还会出现fk中已经出现的项,很显然fk就不是最优的,这也就是为什么说MP收敛就需要更多次迭代的原因。不是说MP一定得到不到最优解,而且其前面描述的特性导致一般得到不到最优解而是次优解。那么,有没有办法让第k个残差与

正交,方法是有的,这就是下面要谈到的OMP算法。
3.OMP算法
3.1 算法描述
OMP算法的改进之处在于:在分解的每一步对所选择的全部原子进行正交化处理,这使得在精度要求相同的情况下,OMP算法的收敛速度更快。
那么在每一步中如何对所选择的全部原子进行正交化处理呢?在正式描述OMP算法前,先看一点基础思想。
先看一个 k 阶模型,表示信号 f 经过 k 步分解后的情况,似乎很眼熟,但要注意它与MP算法不同之处,它的残值与前面每个分量正交,这就是为什么这个算法多了一个正交的原因,MP中仅与最近选出的的那一项正交。
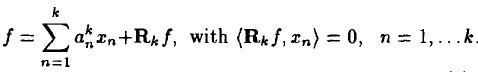
(1)
k + 1 阶模型如下:
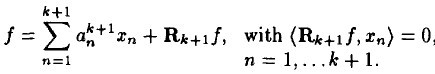
(2)
应用 k + 1阶模型减去k 阶模型,得到如下:
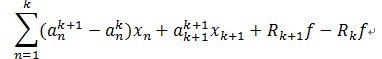
(3)
我们知道,字典矩阵D的原子是非正交的,引入一个辅助模型,它是表示
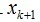
对前k个项
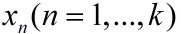
的依赖,描述如下:
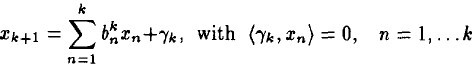
(4)
和前面描述类似,
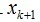
在span(x1, ...xk)之一上的正交投影操作,后面的项是残值。这个关系用数学符号描述:
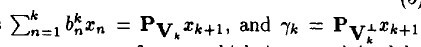
请注意,这里的 a 和 b 的上标表示第 k 步时的取值。
将(4)带入(3)中,有:
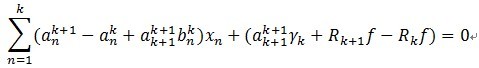
(5)
如果一下两个式子成立,(5)必然成立。
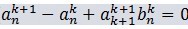
(6)
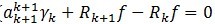
(7)
令
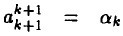
,有
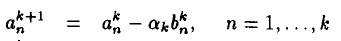
其中
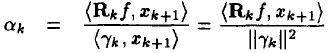
。
ak的值是由求法很简单,通过对(7)左右两边添加
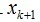
作内积消减得到:
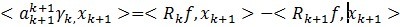
后边的第二项因为它们正交,所以为0,所以可以得出ak的第一部分。对于
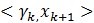
,在(4)左右两边中与

作内积,可以得到ak的第二部分。
对于(4),可以求出
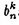
,求的步骤请参见参考文件的计算细节部分。为什么这里不提,因为后面会介绍更简单的方法来计算。
3.2 收敛性证明
通过(7)
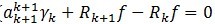
,由于

与
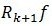
正交,将两个残值移到右边后求二范的平方,并将ak的值代入可以得到:
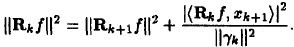
可见每一次残差比上一次残差小,可见是收敛的。
3.3 算法步骤
整个OMP算法的步骤如下:

由于有了上面的来龙去脉,这个算法就相当好理解了。
到这里还不算完,后来OMP的迭代运算用另外一种方法可以计算得知,有位同学的论文[2]描述就非常好,我就直接引用进来:


对比中英文描述,本质都是一样,只是有细微的差别。这里顺便贴出网一哥们写的OMP算法的代码,源出处不得而知,共享给大家。

再贴另外一个洋牛paper[3]中关于OMP的描述,之所以引入,是因为它描述的非常严谨,但是也有点苦涩难懂,不过有了上面的基础,就容易多了。

它的描述中的Sweep步骤就是寻找与当前残差最大的内积时列在字典矩阵D中的索引,它的这个步骤描述说明为什么要选择内积最大的以及如何选择。见下图,说的非常清晰。
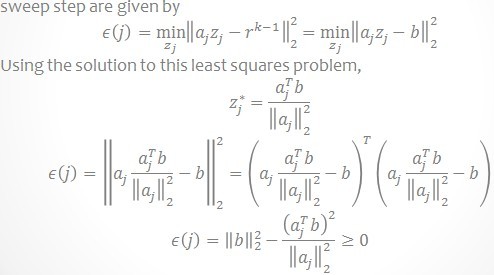
它的算法步骤Update Provisional Solution中求
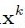
很简单,就是在 b = Ax 已知 A和b求x, 在x的最小二范就是A的伪逆与b相乘,即:
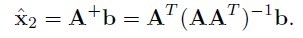
看上去头疼,其实用matlab非常简单,看看上面的matlab的代码就明白了。
我们可以看得出来,算法流程清晰明了,还是很好理解的。这正是OMP算法的魅力,作为工具使用简单,背后却隐藏着很有趣的思想。
写这篇博客的目的,是因为搜索了一下,MP和OMP没有人很详细的介绍。文献[1]讲的很清楚的,大家有兴趣可以找来看看。不要被老板发现我居然在搜中文文献还写中文博客。
参考文献:
[1] Orthogonal Matching Pursuit:Recursive Function Approximat ion with Applications to Wavelet Decomposition
[2]http://wenku.baidu.com/view/22f3171614791711cc7917e4.html
[3] From Sparse Solutions of Systems of Equations to Sparse Modeling of Signals and Images
稀疏编码中的正交匹配追踪(OMP)与代码
最近在看有关匹配追踪与相关优化的文章,发现了这篇http://blog.csdn.net/scucj/article/details/7467955,感觉作者写得很不错,这里也再写写自己的理解。文中有Matlab的代码,为了方便以后的使用,我顺便写了一个C++版本的,方便与OpenCV配合。
为了方便理解,我将所有向量都表示为平面二维向量,待用原子表征的目标向量y,用红色表示,原子向量用蓝色表示,残差向量用绿色表示。于是匹配追踪算法(MP)实际上可以用下图表示。

注意原子向量和目标向量都已归一化到单位长度,MP算法首先在所有原子向量中找到向OA投影最大的向量,即OB,然后计算OA - <OA, OB>OB,其中的<OA, OB>OB也就是图中的OD了,被OA减掉后,剩下的就是残差DA,根据初中几何知识就可以知道,DA是一定垂直于OB的,也就是说MP的残差始终与最近选出来的那个原子向量正交。
而OMP要做的,就是让残差与已经选出来的所有原子向量都正交,这一点在图上不好画出来,但上面的那篇博文写的已经很详尽了,这里不再敖述。
下面是用C++实现的OMP算法,具体流程参考上面博文中的一张图:

其中的最小二乘可以直接通过矩阵运算得到,也可以使用OpenCV的solve方法,该方法专门用于求解线性方程组或最小二乘问题。代码如下:
[cpp] view
plain copy


void OrthMatchPursuit(
vector<Mat>& dic,//字典
Mat& target,
float min_residual,
int sparsity,
Mat& x, //返回每个原子对应的系数;
vector<int>& patch_indices //返回选出的原子序号
)
{
Mat residual = target.clone();
Mat phi; //保存已选出的原子向量
x.create(0, 1, CV_32FC1);
float max_coefficient;
unsigned int patch_index;
for(;;)
{
max_coefficient = 0;
for (int i = 0; i < dic.size(); i++)
{
float coefficient = (float)dic[i].dot(residual);
if (abs(coefficient) > abs(max_coefficient))
{
max_coefficient = coefficient;
patch_index = i;
}
}
patch_indices.push_back(patch_index); //添加选出的原子序号
Mat& matched_patch = dic[patch_index];
if (phi.cols == 0)
phi = matched_patch;
else
hconcat(phi,matched_patch,phi); //将新原子合并到原子集合中(都是列向量)
x.push_back(0.0f); //对系数矩阵新加一项
solve(phi, target, x, DECOMP_SVD); //求解最小二乘问题
residual = target - phi*x; //更新残差
float res_norm = (float)norm(residual);
if (x.rows >= sparsity || res_norm <= min_residual) //如果残差小于阈值或达到要求的稀疏度,就返回
return;
}
}
代码写得有点乱,基本上完全按照算法步骤来的,应该还有很大的性能提升空间。
===================================无耻的分割线========================================
之前说上面的代码还有很大的优化空间,这几天捣鼓了一下,发现优化还是很有成效的,下面是具体方法。
为方便起见,这里用A代表从字典当中选出的原子的集合,对于上面求解最小二乘的一步,可以表示为下式:

其中的

是一个对称正定矩阵,现在假如经过一次搜索后,又找到了一个原子向量v,那么新的原子集合可以表示为:

那么用这个新的原子集合计算x时,可以得到:

可以看到,新的集合乘积,有一部分是上次的结果(上式最右边矩阵的第一个元素),因此没有必要每次都从新计算,而只需对原来的矩阵更新一列和一行就行了。同时,上式的第二和第三个元素互为转置,也只需要计算其中一个,第四个元素是v的二范数的平方,直接调用norm()函数求得。
在对矩阵进行行和列的添加时,我放弃了使用vconcat和hconcat方法,这两个方法效率较低,每次添加都会把原来的部分复制一遍。我现在一次分配好需要的大小,然后通过Mat的括号操作符取需要的子矩阵进行更新和计算。
求解x时,还有一步是求

的逆,既然

是对称正定的,可以进行Cholesky分解,那么它的逆也可以很快求出。刚好OpenCV中有这样的方法,即调用inv()方法时,用DECOMP_CHOLESKY作为参数,根据官方文档,这样的速度是普通矩阵求逆的两倍!
我做了一个测试,使用一个有600多个原子的字典,每个原子的维度为200,稀疏度设定为10,匹配一个信号,原来的方法需要200ms左右,而用上面的方法优化后,只需10ms!!快了一个数量级!!
下面是优化后的代码:
[cpp] view
plain copy


void DictionaryLearning::OrthMatchPursuit(
Mat& target,
float min_residual,
int sparsity,
//Store matched patches' coefficient
vector<float>& coefficients,
//Store matched patches
vector<DicPatch>& matched_patches,
//Store indices of matched patches
vector<int>& matched_indices
)
{
Mat residual = target.clone();
//the atoms' set;
Mat ori_phi = Mat::zeros(m_vec_dims,sparsity,CV_32FC1);
Mat phi;
//phi.t()*phi which is a SPD matrix
Mat ori_spd = Mat::ones(sparsity,sparsity,CV_32FC1);
Mat spd = ori_spd(Rect(0,0,1,1));
//reserve enough memory.
matched_patches.reserve(sparsity);
matched_indices.reserve(sparsity);
float max_coefficient;
int matched_index;
deque<DicPatch>::iterator matched_patch_it;
for(int spars = 1;;spars++)
{
max_coefficient = 0;
matched_index = 0;
int current_index = 0;
for (deque<DicPatch>::iterator patch_it = m_patches.begin();
patch_it != m_patches.end();
++patch_it
)
{
Mat& cur_vec = (*patch_it).vector;
float coefficient = (float)cur_vec.dot(residual);
//Find the maxmum coefficient
if (abs(coefficient) > abs(max_coefficient))
{
max_coefficient = coefficient;
matched_patch_it = patch_it;
matched_index = current_index;
}
current_index++;
}
matched_patches.push_back((*matched_patch_it));
matched_indices.push_back(matched_index);
Mat& matched_vec = (*matched_patch_it).vector;
//update the spd matrix via symply appending a single row and column to it.
if (spars > 1)
{
Mat v = matched_vec.t()*phi;
float c = (float)norm(matched_vec);
Mat new_row = ori_spd(Rect(0, spars - 1, spars - 1, 1));
Mat new_col = ori_spd(Rect(spars - 1, 0, 1, spars - 1));
v.copyTo(new_row);
((Mat)v.t()).copyTo(new_col);
*ori_spd.ptr<float>(spars - 1, spars - 1) = c*c;
spd = ori_spd(Rect(0, 0, spars, spars));
}
//Add the new matched patch to the vectors' set.
phi = ori_phi(Rect(0, 0, spars, m_vec_dims));
matched_vec.copyTo(phi.col(spars - 1));
//A SPD matrix! Use Cholesky process to speed up.
Mat x = spd.inv(DECOMP_CHOLESKY)*phi.t()*target;
residual = target - phi*x;
float res_norm = (float)norm(residual);
if (spars >= sparsity || res_norm <= min_residual)
{
coefficients.clear();
coefficients.reserve(x.cols);
x.copyTo(coefficients);
return;
}
}
}
1. 信号的稀疏表示(sparse representation of signals)
给定一个过完备字典矩阵
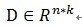
,其中它的每列表示一种原型信号的原子。给定一个信号y,它可以被表示成这些原子的稀疏线性组合。信号 y 可以被表达为 y = Dx ,或者
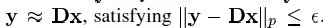
。
字典矩阵中所谓过完备性,指的是原子的个数远远大于信号y的长度(其长度很显然是n),即n<<k。
2.MP算法(匹配追踪算法)
2.1 算法描述
作为对信号进行稀疏分解的方法之一,将信号在完备字典库上进行分解。
假定被表示的信号为y,其长度为n。假定H表示Hilbert空间,在这个空间H里,由一组向量
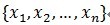
构成字典矩阵D,其中每个向量可以称为原子(atom),其长度与被表示信号 y 的长度n相同,而且这些向量已作为归一化处理,即|
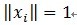
,也就是单位向量长度为1。MP算法的基本思想:从字典矩阵D(也称为过完备原子库中),选择一个与信号
y 最匹配的原子(也就是某列),构建一个稀疏逼近,并求出信号残差,然后继续选择与信号残差最匹配的原子,反复迭代,信号y可以由这些原子来线性和,再加上最后的残差值来表示。很显然,如果残差值在可以忽略的范围内,则信号y就是这些原子的线性组合。如果选择与信号y最匹配的原子?如何构建稀疏逼近并求残差?如何进行迭代?我们来详细介绍使用MP进行信号分解的步骤:[1] 计算信号 y 与字典矩阵中每列(原子)的内积,选择绝对值最大的一个原子,它就是与信号 y 在本次迭代运算中最匹配的。用专业术语来描述:令信号
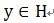
,从字典矩阵中选择一个最为匹配的原子,满足
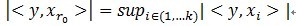
,r0
表示一个字典矩阵的列索引。这样,信号 y 就被分解为在最匹配原子
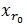
的垂直投影分量和残值两部分,即:
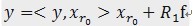
。[2]对残值R1f进行步骤[1]同样的分解,那么第K步可以得到:
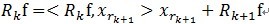
, 其中
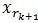
满足
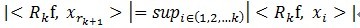
。可见,经过K步分解后,信号
y 被分解为:

,其中
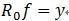
。
2.2 继续讨论
(1)为什么要假定在Hilbert空间中?Hilbert空间就是定义了完备的内积空。很显然,MP中的计算使用向量的内积运算,所以在在Hilbert空间中进行信号分解理所当然了。什么是完备的内积空间?篇幅有限就请自己搜索一下吧。
(2)为什么原子要事先被归一化处理了,即上面的描述
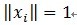
。内积常用于计算一个矢量在一个方向上的投影长度,这时方向的矢量必须是单位矢量。MP中选择最匹配的原子是,是选择内积最大的一个,也就是信号(或是残值)在原子(单位的)垂直投影长度最长的一个,比如第一次分解过程中,投影长度就是
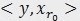
。
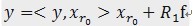
,三个向量,构成一个三角形,且
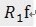
和
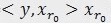
正交(不能说垂直,但是可以想象二维空间这两个矢量是垂直的)。
(3)MP算法是收敛的,因为
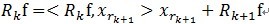
,
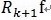
和
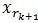
正交,由这两个可以得出
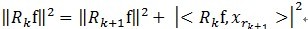
,得出每一个残值比上一次的小,故而收敛。
2.3 MP算法的缺点
如上所述,如果信号(残值)在已选择的原子进行垂直投影是非正交性的,这会使得每次迭代的结果并不少最优的而是次最优的,收敛需要很多次迭代。举个例子说明一下:在二维空间上,有一个信号 y 被 D=[x1, x2]来表达,MP算法迭代会发现总是在x1和x2上反复迭代,即
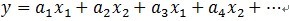
,这个就是信号(残值)在已选择的原子进行垂直投影的非正交性导致的。再用严谨的方式描述[1]可能容易理解:在Hilbert空间H中,
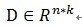
,
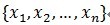
,定义
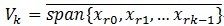
,就是它是这些向量的张成中的一个,MP构造一种表达形式:
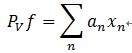
;这里的Pvf表示
f在V上的一个正交投影操作,那么MP算法的第 k 次迭代的结果可以表示如下(前面描述时信号为y,这里变成f了,请注意):
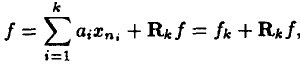
如果

是最优的k项近似值,当且仅当
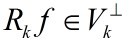
。由于MP仅能保证
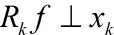
,所以

一般情况下是次优的。这是什么意思呢?

是k个项的线性表示,这个组合的值作为近似值,只有在第k个残差和

正交,才是最优的。如果第k个残值与

正交,意味这个残值与fk的任意一项都线性无关,那么第k个残值在后面的分解过程中,不可能出现fk中已经出现的项,这才是最优的。而一般情况下,不能满足这个条件,MP一般只能满足第k个残差和xk正交,这也就是前面为什么提到“信号(残值)在已选择的原子进行垂直投影是非正交性的”的原因。如果第k个残差和fk不正交,那么后面的迭代还会出现fk中已经出现的项,很显然fk就不是最优的,这也就是为什么说MP收敛就需要更多次迭代的原因。不是说MP一定得到不到最优解,而且其前面描述的特性导致一般得到不到最优解而是次优解。那么,有没有办法让第k个残差与

正交,方法是有的,这就是下面要谈到的OMP算法。
3.OMP算法
3.1 算法描述
OMP算法的改进之处在于:在分解的每一步对所选择的全部原子进行正交化处理,这使得在精度要求相同的情况下,OMP算法的收敛速度更快。
那么在每一步中如何对所选择的全部原子进行正交化处理呢?在正式描述OMP算法前,先看一点基础思想。
先看一个 k 阶模型,表示信号 f 经过 k 步分解后的情况,似乎很眼熟,但要注意它与MP算法不同之处,它的残值与前面每个分量正交,这就是为什么这个算法多了一个正交的原因,MP中仅与最近选出的的那一项正交。
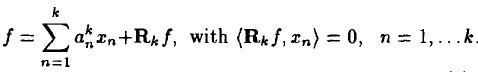
(1)
k + 1 阶模型如下:
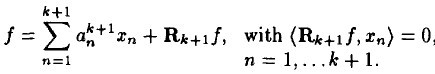
(2)
应用 k + 1阶模型减去k 阶模型,得到如下:
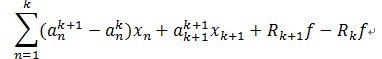
(3)
我们知道,字典矩阵D的原子是非正交的,引入一个辅助模型,它是表示
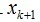
对前k个项
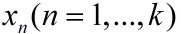
的依赖,描述如下:
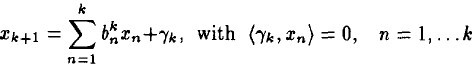
(4)
和前面描述类似,
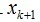
在span(x1, ...xk)之一上的正交投影操作,后面的项是残值。这个关系用数学符号描述:
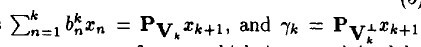
请注意,这里的 a 和 b 的上标表示第 k 步时的取值。
将(4)带入(3)中,有:
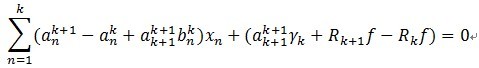
(5)
如果一下两个式子成立,(5)必然成立。
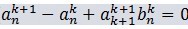
(6)
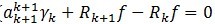
(7)
令
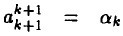
,有
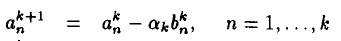
其中
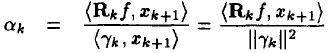
。
ak的值是由求法很简单,通过对(7)左右两边添加
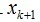
作内积消减得到:
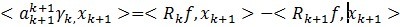
后边的第二项因为它们正交,所以为0,所以可以得出ak的第一部分。对于
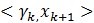
,在(4)左右两边中与

作内积,可以得到ak的第二部分。
对于(4),可以求出
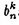
,求的步骤请参见参考文件的计算细节部分。为什么这里不提,因为后面会介绍更简单的方法来计算。
3.2 收敛性证明
通过(7)
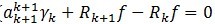
,由于

与
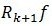
正交,将两个残值移到右边后求二范的平方,并将ak的值代入可以得到:
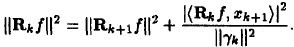
可见每一次残差比上一次残差小,可见是收敛的。
3.3 算法步骤
整个OMP算法的步骤如下:

由于有了上面的来龙去脉,这个算法就相当好理解了。
到这里还不算完,后来OMP的迭代运算用另外一种方法可以计算得知,有位同学的论文[2]描述就非常好,我就直接引用进来:


对比中英文描述,本质都是一样,只是有细微的差别。这里顺便贴出网一哥们写的OMP算法的代码,源出处不得而知,共享给大家。

再贴另外一个洋牛paper[3]中关于OMP的描述,之所以引入,是因为它描述的非常严谨,但是也有点苦涩难懂,不过有了上面的基础,就容易多了。

它的描述中的Sweep步骤就是寻找与当前残差最大的内积时列在字典矩阵D中的索引,它的这个步骤描述说明为什么要选择内积最大的以及如何选择。见下图,说的非常清晰。
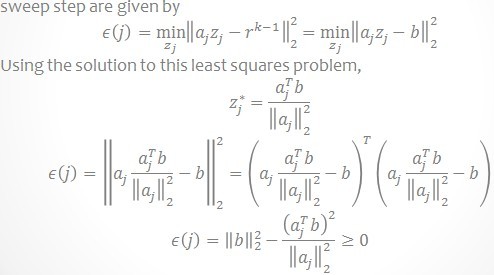
它的算法步骤Update Provisional Solution中求
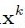
很简单,就是在 b = Ax 已知 A和b求x, 在x的最小二范就是A的伪逆与b相乘,即:
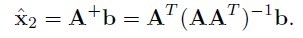
看上去头疼,其实用matlab非常简单,看看上面的matlab的代码就明白了。
我们可以看得出来,算法流程清晰明了,还是很好理解的。这正是OMP算法的魅力,作为工具使用简单,背后却隐藏着很有趣的思想。
写这篇博客的目的,是因为搜索了一下,MP和OMP没有人很详细的介绍。文献[1]讲的很清楚的,大家有兴趣可以找来看看。不要被老板发现我居然在搜中文文献还写中文博客。
参考文献:
[1] Orthogonal Matching Pursuit:Recursive Function Approximat ion with Applications to Wavelet Decomposition
[2]http://wenku.baidu.com/view/22f3171614791711cc7917e4.html
[3] From Sparse Solutions of Systems of Equations to Sparse Modeling of Signals and Images
稀疏编码中的正交匹配追踪(OMP)与代码
最近在看有关匹配追踪与相关优化的文章,发现了这篇http://blog.csdn.net/scucj/article/details/7467955,感觉作者写得很不错,这里也再写写自己的理解。文中有Matlab的代码,为了方便以后的使用,我顺便写了一个C++版本的,方便与OpenCV配合。
为了方便理解,我将所有向量都表示为平面二维向量,待用原子表征的目标向量y,用红色表示,原子向量用蓝色表示,残差向量用绿色表示。于是匹配追踪算法(MP)实际上可以用下图表示。

注意原子向量和目标向量都已归一化到单位长度,MP算法首先在所有原子向量中找到向OA投影最大的向量,即OB,然后计算OA - <OA, OB>OB,其中的<OA, OB>OB也就是图中的OD了,被OA减掉后,剩下的就是残差DA,根据初中几何知识就可以知道,DA是一定垂直于OB的,也就是说MP的残差始终与最近选出来的那个原子向量正交。
而OMP要做的,就是让残差与已经选出来的所有原子向量都正交,这一点在图上不好画出来,但上面的那篇博文写的已经很详尽了,这里不再敖述。
下面是用C++实现的OMP算法,具体流程参考上面博文中的一张图:

其中的最小二乘可以直接通过矩阵运算得到,也可以使用OpenCV的solve方法,该方法专门用于求解线性方程组或最小二乘问题。代码如下:
[cpp] view
plain copy


void OrthMatchPursuit(
vector<Mat>& dic,//字典
Mat& target,
float min_residual,
int sparsity,
Mat& x, //返回每个原子对应的系数;
vector<int>& patch_indices //返回选出的原子序号
)
{
Mat residual = target.clone();
Mat phi; //保存已选出的原子向量
x.create(0, 1, CV_32FC1);
float max_coefficient;
unsigned int patch_index;
for(;;)
{
max_coefficient = 0;
for (int i = 0; i < dic.size(); i++)
{
float coefficient = (float)dic[i].dot(residual);
if (abs(coefficient) > abs(max_coefficient))
{
max_coefficient = coefficient;
patch_index = i;
}
}
patch_indices.push_back(patch_index); //添加选出的原子序号
Mat& matched_patch = dic[patch_index];
if (phi.cols == 0)
phi = matched_patch;
else
hconcat(phi,matched_patch,phi); //将新原子合并到原子集合中(都是列向量)
x.push_back(0.0f); //对系数矩阵新加一项
solve(phi, target, x, DECOMP_SVD); //求解最小二乘问题
residual = target - phi*x; //更新残差
float res_norm = (float)norm(residual);
if (x.rows >= sparsity || res_norm <= min_residual) //如果残差小于阈值或达到要求的稀疏度,就返回
return;
}
}
代码写得有点乱,基本上完全按照算法步骤来的,应该还有很大的性能提升空间。
===================================无耻的分割线========================================
之前说上面的代码还有很大的优化空间,这几天捣鼓了一下,发现优化还是很有成效的,下面是具体方法。
为方便起见,这里用A代表从字典当中选出的原子的集合,对于上面求解最小二乘的一步,可以表示为下式:

其中的

是一个对称正定矩阵,现在假如经过一次搜索后,又找到了一个原子向量v,那么新的原子集合可以表示为:

那么用这个新的原子集合计算x时,可以得到:

可以看到,新的集合乘积,有一部分是上次的结果(上式最右边矩阵的第一个元素),因此没有必要每次都从新计算,而只需对原来的矩阵更新一列和一行就行了。同时,上式的第二和第三个元素互为转置,也只需要计算其中一个,第四个元素是v的二范数的平方,直接调用norm()函数求得。
在对矩阵进行行和列的添加时,我放弃了使用vconcat和hconcat方法,这两个方法效率较低,每次添加都会把原来的部分复制一遍。我现在一次分配好需要的大小,然后通过Mat的括号操作符取需要的子矩阵进行更新和计算。
求解x时,还有一步是求

的逆,既然

是对称正定的,可以进行Cholesky分解,那么它的逆也可以很快求出。刚好OpenCV中有这样的方法,即调用inv()方法时,用DECOMP_CHOLESKY作为参数,根据官方文档,这样的速度是普通矩阵求逆的两倍!
我做了一个测试,使用一个有600多个原子的字典,每个原子的维度为200,稀疏度设定为10,匹配一个信号,原来的方法需要200ms左右,而用上面的方法优化后,只需10ms!!快了一个数量级!!
下面是优化后的代码:
[cpp] view
plain copy


void DictionaryLearning::OrthMatchPursuit(
Mat& target,
float min_residual,
int sparsity,
//Store matched patches' coefficient
vector<float>& coefficients,
//Store matched patches
vector<DicPatch>& matched_patches,
//Store indices of matched patches
vector<int>& matched_indices
)
{
Mat residual = target.clone();
//the atoms' set;
Mat ori_phi = Mat::zeros(m_vec_dims,sparsity,CV_32FC1);
Mat phi;
//phi.t()*phi which is a SPD matrix
Mat ori_spd = Mat::ones(sparsity,sparsity,CV_32FC1);
Mat spd = ori_spd(Rect(0,0,1,1));
//reserve enough memory.
matched_patches.reserve(sparsity);
matched_indices.reserve(sparsity);
float max_coefficient;
int matched_index;
deque<DicPatch>::iterator matched_patch_it;
for(int spars = 1;;spars++)
{
max_coefficient = 0;
matched_index = 0;
int current_index = 0;
for (deque<DicPatch>::iterator patch_it = m_patches.begin();
patch_it != m_patches.end();
++patch_it
)
{
Mat& cur_vec = (*patch_it).vector;
float coefficient = (float)cur_vec.dot(residual);
//Find the maxmum coefficient
if (abs(coefficient) > abs(max_coefficient))
{
max_coefficient = coefficient;
matched_patch_it = patch_it;
matched_index = current_index;
}
current_index++;
}
matched_patches.push_back((*matched_patch_it));
matched_indices.push_back(matched_index);
Mat& matched_vec = (*matched_patch_it).vector;
//update the spd matrix via symply appending a single row and column to it.
if (spars > 1)
{
Mat v = matched_vec.t()*phi;
float c = (float)norm(matched_vec);
Mat new_row = ori_spd(Rect(0, spars - 1, spars - 1, 1));
Mat new_col = ori_spd(Rect(spars - 1, 0, 1, spars - 1));
v.copyTo(new_row);
((Mat)v.t()).copyTo(new_col);
*ori_spd.ptr<float>(spars - 1, spars - 1) = c*c;
spd = ori_spd(Rect(0, 0, spars, spars));
}
//Add the new matched patch to the vectors' set.
phi = ori_phi(Rect(0, 0, spars, m_vec_dims));
matched_vec.copyTo(phi.col(spars - 1));
//A SPD matrix! Use Cholesky process to speed up.
Mat x = spd.inv(DECOMP_CHOLESKY)*phi.t()*target;
residual = target - phi*x;
float res_norm = (float)norm(residual);
if (spars >= sparsity || res_norm <= min_residual)
{
coefficients.clear();
coefficients.reserve(x.cols);
x.copyTo(coefficients);
return;
}
}
}
相关文章推荐
- MP算法和OMP算法及其思想
- MP算法和OMP算法及其思想
- MP算法和OMP算法及其思想
- MP算法和OMP算法及其思想
- MP算法和OMP算法及其思想
- MP算法和OMP算法及其思想
- MP算法和OMP算法及其思想
- MP算法和OMP算法及其思想
- MP算法和OMP算法及其思想
- MP算法和OMP算法及其思想
- MP算法和OMP算法及其思想
- MP算法和OMP算法及其思想
- MP算法和OMP算法及其思想
- MP算法和OMP算法及其思想
- MP算法和OMP算法及其思想 分类: 机器学习 2014-08-16 10:50 116人阅读 评论(0) 收藏
- MP算法和OMP算法及其思想
- MP算法和OMP算法及其思想
- MP算法和OMP算法及其思想
- MP算法和OMP算法及其思想
- MP算法和OMP算法及其思想
