第二课 监督学习应用 梯度下降

1. 最小均方误差算法

h(x) 为目标函数

θ 为参数parameters

xn为特征

n为特征个数

m为训练集的个数

则在线性假设下

h(x)=hθ(x)=θ0+θ1∗x1+θ2∗x2+...+θn∗xn

即

h(x)=hθ(x)=∑i=0nθi∗xi=ΘTX

根据训练集（training sets）求出Θ

其中一种方法为最小二乘方（LMS，least mean squares）：

minθ J(θ)

其中

J(θ)=12∑i=1n(hθ(xi)−yi)2

表示估计值与真实值之间的误差

计算求解θ的一种方法为梯度下降法：



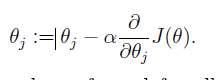
考虑只有一个样本点时





重复对上式计算，直到θ值不变时，结果收敛。

其中，α为调整收敛速度大小的参数，该算法结果与初始值的设定有关，结果可能是局部最优解（local optimal）。在线性假设下，该结果为全局最优解。

将该方法拓展到对个训练对象时，有两种梯度下降方法，第一种叫做批量梯度下降(batch gradient descent)：



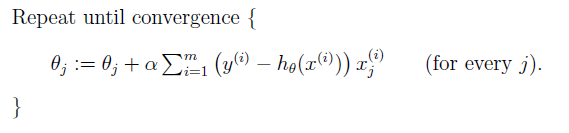
该方法最小化所有训练样本的损失函数，使得最终求解的是全局的最优解，即求解的参数是使得风险函数最小。计算量大

另外一种叫做随机梯度下降(stochastic gradient descent)：



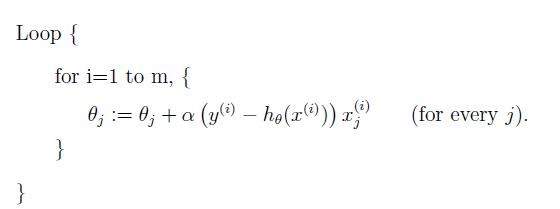
该方法最小化每条样本的损失函数，虽然不是每次迭代得到的损失函数都向着全局最优方向， 但是大的整体的方向是向全局最优解的，最终的结果往往是在全局最优解附近。计算量小

2.一些常见方程

2.1矩阵微分

矩阵微分的符号为：



迹的符号为



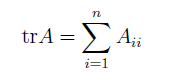
关于矩阵迹的一些性质









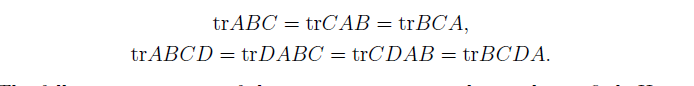
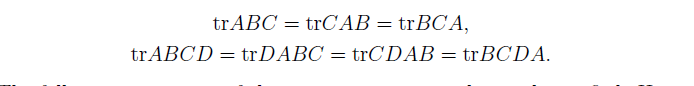
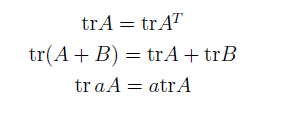
这些性质可以自己证明

2.2再探最小均方差

下面将用矩阵运算的思想来求解最小均方差的解

首先把目标函数使用矩阵形式表示







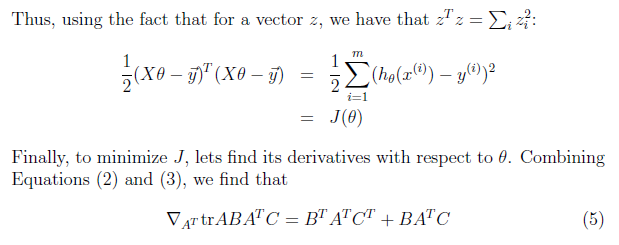
上式证明，将问题矩阵化后，导数为0，可以求出θ的值