最佳子集选择，岭回归，套索的比较

套索（Lasso）

Lasso也是一种收缩方法，Lasso估计的定义如下:

β^lasso=argminβ∑Ni=1(yi−β0−∑pj=1xijβj)2

subject to∑pj=1|βj|<=t

通过对数据标准化去除截距项，也可以将Lasso写成如下形式：

β^lasso=argminβ{∑Ni=1(yi−β0−∑pj=1xijβj)2+λ∑pj=1|βj|}

罚∑pj=1|βj|使得回归的估计在y上不是线性的，可以使用二次规划算法计算。

最佳子集选择，岭回归，套索的比较

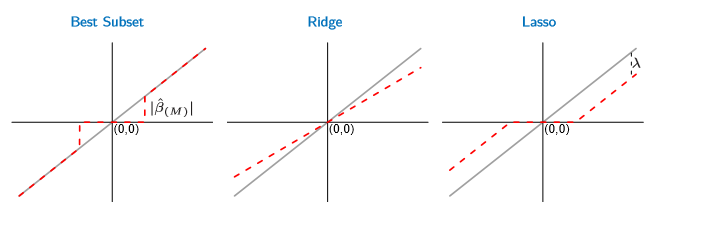
首先考虑输入是正交的情况，在这种情况下观察这三种方法的特点

可以证明，对于正交输入，这三种方法有显示解，每一种方法都对ols的估计β^做了某种变换，具体来说：

对于子集选择，将选择绝对值最大的M个ols的系数，这比较好理解，因为子集选择要选择与残差最相关的M个方向，这样才能使残差和最小。

对于岭回归，由岭回归的估计

β^ridge=(XTX+λI)−1XTy=1(λ+1)XTy

可以知道岭回归相当于将每个系数收缩为原来的1(λ+1)倍。

对于Lasso，

系数变为sign(β^j)(|β^j|−λ)+,也就是说对于绝对值小于λ的系数收缩到0，对于大于等于λ的系数则减去λ。

这三种方法的系数改变情况如下图所示：



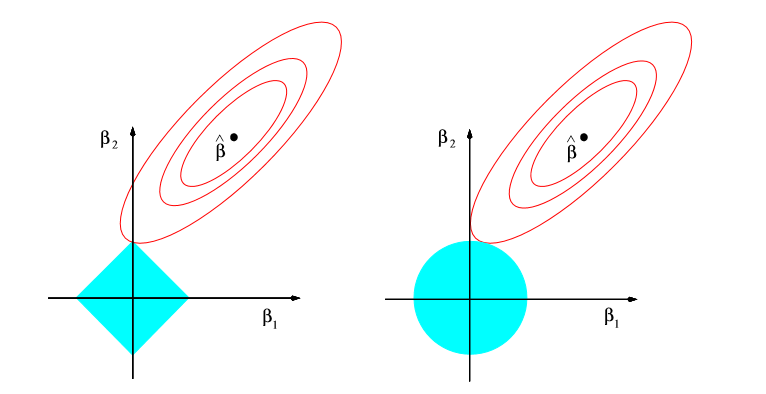
进一步考察Lasso和岭回归的特点，考虑二维输入的情况，可以画出使得残差平方和 和β的取值情况，首先残差平方和的等值线是椭圆，中心是ols的估计，

对于岭回归，限制条件使得β的取值区域是一个圆，而对于lasso来说取值区域是一个正方形，可以看到，对于正方形来说，等值线更可能触及到顶点，所以对于Lasso更容易将系数收缩到0，对于多维输入也是这样，Lasso有更大的机会将系数收缩到0，这是一个很好的性质。

贝叶斯角度

上一篇博客里证明了岭回归可以从贝叶斯估计的导出，更一般的，将Lasso和岭回归推广，考虑如下准则

β^=argminβ∑Ni=1(yi−β0−∑pj=1xijβj)2+λ∑pj=1|βj|q

这里把λ∑pj=1|βj|q看成参数的对数先验密度

可以看到，当q为零时就是最佳子集选择，q为1时就是Lasso，q为2是就是岭回归，从贝叶斯估计的角度来看，这三种方法是从不同的先验分布来估计参数，参数的估计值是后验分布的众数，也就是使得后验最大的参数值。对于岭回归来说，参数的后验的平均值和众数相等，但对于其他情况就不一定这样了。