算法整理——非对称密钥加密RSA数学相关与简单实现

RSA

   RSA公钥加密算法是1977年由Ron Rivest、Adi Shamir和Leonard Adleman一起提出的，是目前最有影响力的公钥加密算法，能够抵抗到目前为止已知的绝大多数密码攻击。RSA算法基于一个十分简单的数论事实：将两个大质数相乘十分容易，但是想要对其乘积进行因式分解却极其困难。RSA算法是第一个能同时用于加密和数字签名的算法，也易于理解和操作。加密方式是发送者采用接收者的公钥加密，而这个公钥是公开的，任何人都可以知道。接收者利用自己私钥对密文进行解密，因为私钥只有自己知道，此时别人拿到密文以及公钥都无法解出原文。签名方式则反过来，签名者使用私钥签名，查看者只需要使用公钥进行解密。一旦解出的原文消息符合预期，签名者则无法反驳自己曾对这段密文进行签名，因为私钥只有它自己有。

数学基础

欧拉定理

RSA算法的理论基础基于以下的数学推导式



什么情况下(e1, e2, n 关系)才能使得最后一个式子成立？欧拉定理给出了答案：

 欧拉定理表明，若n, a为正整数，且互素，则有
 


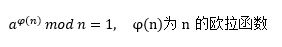
（欧拉函数φ(n)：在数论，对正整数n，欧拉函数是小于n的数中与n互质的数的数目。）

关于欧拉定理的证明，来自 某百科

将1~n中与n互质的数按顺序排布：x1, x2, ……, xφ(n) （显然，共有φ(n)个数）

我们考虑这么一些数：

m1=a*x1, m2=a*x2, m3=a*x3, ……, mφ(n)=a*xφ(n)

1）这些数中的任意两个都不模n同余，因为如果有mS≡mR (mod n) （这里假定mS更大一些），就有：

mS-mR=a(xS-xR)=qn（q为一整数，两者模n同余，在相减之后余数减去，剩余部分将是n的倍数），即n能整除a(xS-xR)。但是a与n互质，a与n的最大公因子是1（此时最小公倍数为a*n），而xS-xR<n（xS, xR均在1~n中），因而左式不可能被n整除。也就是说这些数中的任意两个都不模n同余，φ(n)个数有φ(n)种余数。

2）这些数除n的余数都与n互质，因为如果余数与n有公因子r，那么a*xi=pn+qr=r(……)（这样，a*xi 与 n也将有公因子r），a*xi与n不互质，而这是不可能的。那么这些数除n的余数，都在x1, x2, x3, ……, xφ(n)中，因为这是1~n中与n互质的所有数，而余数又小于n。

由1）和2）可知，数m1, m2, m3, ……, mφ(n)（次序重新排列）必须相应地同余于x1, x2, x3, ……, xφ(n).

故得出：m1*m2*m3……mφ(n)≡x1*x2*x3……xφ(n) (mod n)

或者说：a^[φ(n)]*(x1*x2*x3……xφ(n))≡x1*x2*x3……xφ(n)

或者为了方便：K{a^[φ(n)]-1}≡0 ( mod n ) 这里K=x1*x2*x3……xφ(n)。（模运算交换律）

可知K{a^[φ(n)]-1}被n整除。但K中的因子x1, x2, …… , xφ(n)都与n互质，所以K与n互质。那么a^[φ(n)]-1必须能被n整除，即a^[φ(n)]-1≡0 （mod n），即a^[φ(n)]≡1 （mod n），得证。

由欧拉定理将得到以下一系列的推导：



此时，e1与e2在缩系Zn*中互为乘法的逆，e2可记为e1^(-1)，因为e1*e1^(-1) mod φ(n) = 1 mod φ(n) = 1

所以，对于一个给定的n，只要找到相应的e1, e2就可以进行分对称密钥加密了。但由于RSA安全性的保证——将两个大质数相乘十分容易，但是想要对其乘积进行因式分解却极其困难，一般实际应用情况下，n是两个大质数相乘的结果，而e1 与  φ(n) 互质，因为这样才能保证e2的唯一性。

由此，得出了RSA密钥生成与加密的步骤：

1）找到两个相差较大的大质数，p, q;

2）使 n = p * q，此时n的欧拉函数为 φ(n) = (p-1)(q-1);

3）在 1 ~ φ(n)中找到与 φ(n)互质的e1;

4）通过关系式找到 满足e1 * e2 mod  φ(n) = 1的e2;

5）组成密钥对，公钥（e1, n），私钥(e2, n)

6）加密采用公钥 B = A^e1 mod n

7）解密采用私钥 A = B^e2 mod n

代码

以下贴出几个在使用RSA会应用的高效算法，借鉴自《算法竞赛入门经典》

求最大公约数，理论来自于欧几里得算法，相似地有辗转相除法

该算法有一个拓展// 最大公约数，欧几里得
// 原始算法
int gcdOrigin(int a, int b){
return b == 0 ? a: gcdOrigin(b, a%b);
}

// 拓展
// ax + by = d 使得 |x|+|y|最小
void gcdEx(int a, int b, int& d, int& x, int& y){
if(!b){
d=a;
x = 1;
y = 0;
}else{
gcdEx(b, a%b, d, y, x);
y -= x*(a/b);
}
}
求n的欧拉函数，由于RSA是先找两个大质数p, q，而它们的乘积n的欧拉函数很容易计算出来的，φ(n) = (p-1)(q-1)。但不妨学习情况下计算欧拉函数的方式。

它基于一个数学式：



其中px为大于1不大于n，且与n非互素的整数。

// 计算n的欧拉函数
int eulerPhi(int n){
int m = (int)sqrt(n+0.5);
int ans = n;
for(int i = 2; i <= m ; i++){
if(n % i == 0){
ans = ans/i *(i-1);
while(n % i ==0)
n/=i;
}
}
if(n > 1)
ans = ans/n *(n-1);
}

求乘法逆，该算法十分重要，主要运用了欧几里得拓展算法式子 ax+by = d。
让e1 = a, b = φ(n) ，一旦算出 d为1，时，说明e1与φ(n) 互质，e2为 x mod φ(n) 。因为 e1e2 + φ(n) y = 1, 即 e1e2 = 1 - φ(n) y, e1e2 mod φ(n)  = (1-φ(n) y) mod φ(n)  = 1。

// 求乘法逆，不存在时返回-1
int inv(int a, int b){
int d, x, y;
gcdEx(a,b,d,x,y);
return d==1?(x+b)%b:-1;
}

快速幂取模，加解密阶段用到

// (a^pow) mod n
int fastPowMod(int a, int pow, int n){
int ans = 1;
int iter = a; //迭代
while(pow){
if(pow & 0x1){
ans = (ans * (iter % n)) % n;
}
iter = (iter * iter) % n ;
pow = pow >> 1;
}
return ans;
}

以下是使用小质数进行的实现，只为简单演示一下过程。但其实RSA的真正的难点是——大数的操作。

运行时p, q请使用百位下的质数，否则取模容易溢出。

//============================================================================
// Name : test.cpp
// Author :
// Version :
// Copyright : Your copyright notice
// Description : Hello World in C++, Ansi-style
//============================================================================

#include <iostream>
#include <cmath>
using namespace std;

// 最大公约数，欧几里得
// 原始算法
int gcdOrigin(int a, int b){
return b == 0 ? a: gcdOrigin(b, a%b);
}

// 拓展
// ax + by = d 使得 |x|+|y|最小
void gcdEx(int a, int b, int& d, int& x, int& y){
if(!b){
d=a;
x = 1;
y = 0;
}else{
gcdEx(b, a%b, d, y, x);
y -= x*(a/b);
}
}

// 检查是否素数
// 小整数
bool checkPrime(int n){
int m = (int) sqrt(n+0.5);
for(int i = 2; i <=m ; i++){
if(n%i==0){
return false;
}
}
return true;
}

// 求剩余集中的 逆
int inv(int a, int b){
int d, x, y;
gcdEx(a,b,d,x,y);
return d==1?(x+b)%b:-1;
}

// 获取 e1, e2
void findE(int& e1, int& e2, int fn){
int m = (int)sqrt(fn);
for(int i = m; i > 1 ; i--){
if(gcdOrigin(fn,i)==1){
//互质
// 求逆 e2
e2 = inv(i,fn);
if(e2==-1){
continue;
}else{
e1 = i ;
return;
}
}
}
e2 = -1;
}

// (a^pow) mod n
int fastPowMod(int a, int pow, int n){
int ans = 1;
int iter = a; //迭代
while(pow){
if(pow & 0x1){
ans = (ans * (iter % n)) % n;
}
iter = (iter * iter) % n ;
pow = pow >> 1;
}
return ans;
}
// 加密
int encrypte(int plaintext, int e1, int n){
return fastPowMod(plaintext, e1, n);
}

// 解密
int decrypte(int ciphertext, int e2, int n){
return fastPowMod(ciphertext, e2, n);
}

int main() {
int p, q, n, e1, e2;
cout << "input two primes:";
cin >> p >> q;
if(!checkPrime(p)||!checkPrime(q)){
cout << "error input, try again" << endl;
return 0;
}

n = p*q;

int fn = (p-1)*(q-1);
findE(e1, e2, fn);

if(e2 ==-1){
cout << "can't find e1, e2." << endl;
}

cout <<"n:"<< n <<" fn:"<< fn << " e1:" << e1 << " e2:" << e2 << endl;

int plaintext, ciphertext;
while(true){
cout << "input plaintext:";
cin >> plaintext;
if(plaintext==0)
break;
ciphertext = encrypte(plaintext, e1, n);
cout << "after encryption:" << ciphertext << endl;
cout << "after decryption:" << decrypte(ciphertext, e2, n) << endl ;
}
return 0;
}

运行

input two primes:193 79

n:15247 fn:14976 e1:121 e2:1609

input plaintext:65

after encryption:9897

after decryption:65

input plaintext:584

after encryption:3645

after decryption:584

input plaintext:3412

after encryption:7203

after decryption:3412

input plaintext:5000

after encryption:8792

after decryption:5000