线性判别分析（Linear Discriminant Analysis）

线性判别分析（Linear Discriminant Analysis）

标签（空格分隔）： 监督学习

@author : duanxxnj@163.com

@time : 2016-07-11

线性判别分析Linear Discriminant Analysis
线性分类器
判别式函数discriminant functions

从判别式或后验概率到决策面

线性判别分析Linear Discriminant Analysis
二次判别分析QDA

Fisher判别式
类间距离

类内距离

Fisher线性判别式

线性分类器

所谓分类器，一般是将输入空间X，根据需要划分的类别，将输入空间划分为一些互不相交的区域，这些区域的边界一般叫做决策面（decision boundaries）。预测函数的形式不同，会使得决策面或者光滑，或者粗糙。其中有一种比较特别的就是判别面是参数的线性函数的，称为线性决策面，形成的分类器就是线性分类器。

判别式函数（discriminant functions）

在讲分类器的时候，肯定会遇到判别式函数这个概念。分类器会为每个类别分配一个判别函数，根据判别函数来判断一个新的样本是否是这个类别的。比如，假设有K个类别，那么分类器肯定会得到K个判别函数 δk(x);k∈[1,2,…,K]。如果有一个新的样本x，那么一般是找到最大的δk(x)，就可以认为，新的样本属于第 k 类。

在一般的分类器中，判别式函数δk(x)，和后验概率P(Ck|x)是对应的，能够使判别式的结果最大，同样也是能够使得样本x在类别Ck下的后验概率最大。

判别式函数δk(x)和δl(x) 相等的点集，就是我们常说的决策面:

δk(x)=δl(x)

从判别式或后验概率到决策面

在判别式函数δk(x)或者后验概率函数P(Ck|x)上加上一个单调函数f(⋅)后，使得变换后的函数是x的线性函数，那么其得到的决策便也是线性的，就可以得到一个线性分类器。

以Logistics Regression为例，假设面对的是一个二分类问题，在Logistics Regression中，是定义类别的后验概率为：

P(C1|x)=11+exp(wTx)P(C2|x)==exp(wTx)1+exp(wTx)

这里，使用一个单调的变换函数，logit 函数：log[p/(1−p)]，那么就可以得到：

logP(C1|x)P(C2|x)=wTx

所以Logistics Regression的决策面就是：wTx=0

凡是分类算法，必定有决策面，而这些分类算法所不同的是:决策面是线性的还是非线性的；以及如果得到这个决策面。

线性判别分析（Linear Discriminant Analysis）

在分类器的理论中，贝叶斯分类器是最优的分类器，而为了得到最优的分类器，我们就需要知道类别的后验概率P(Ck|x)。

这里假设fk(x)是类别Ck的类条件概率密度函数，πk 是类别Ck的先验概率，毫无疑问有∑kπk=1。根据贝叶斯理论有：

P(Ck|x)=fk(x)πk∑Kl=1fl(x)πl

由于πk 几乎是已知的，所以对于贝叶斯公式而言，最重要的就是这个类条件概率密度函数fk(x)，很多算法之所以不同，主要的就是对这个类条件概率密度函数的参数形式的假设不同，比如：

线性判别分析（LDA）假设fk(x)是均值不同，方差相同的高斯分布

二次判别分析（QDA）假设fk(x)是均值不同，方差也不同的高斯分布

高斯混合模型（GMM）假设fk(x)是不同的高斯分布的组合

很多非参数方法假设fk(x)是参数的密度函数，比如直方图

朴素贝叶斯假设fk(x)是Ck边缘密度函数，即类别之间是独立同分布的

各种算法的不同，基本上都是来至于对类条件概率密度函数的不同，这一点在研究分类算法的时候，一定要铭记在心。

前面已经说过了LDA假设fk(x)是均值不同，方差相同的高斯分布，所以其类条件概率密度函数可以写为：

fk(x)=1(2π)p/2|Σ|1/2exp(−12(x−μk)TΣ−1(x−μk))

这里，特征x的维度为p维，类别Ck的均值为μk，所有类别的方差为Σ。

在前面提到过，一个线性分类器，在判别式函数δk(x)或者后验概率函数P(Ck|x)上加上一个单调函数f(⋅)后，可以得变换后的函数是x的线性函数，而得到的线性函数就是决策面。LDA所采用的单调变换函数f(⋅)和前面提到的Logistics Regression采用的单调变换函数一样，都是logit 函数：log[p/(1−p)]，对于二分类问题有：

logP(C1|x)P(C2|x)=logf1(x)f2(x)+logπ1π2=xTΣ−1(μ1−μ2)−12(μ1+μ2)TΣ−1(μ1−μ2)+logπ1π2

可以看出，其决策面是一个平面。

根据上面的式子，也可以很容易得到LDA的决策函数是：

δk(x)=xTΣ−1μk−12μTkΣ−1μk+logπk

其中的参数都是从数据中估计出来的：

πk=Nk/N，Nk是类别Ck的样本数，N是总的样本数。

μk=1Nk∑x∈Ckx ，就是类别Ck的样本均值

Σ=1N−K∑Kk=1∑x∈Ck(x−μk)(x−μk)T

二次判别分析QDA

二次判别函数假设fk(x)是均值不同，方差也不同的高斯分布，和LDA相比，由于Σk是不一样 ，所以其二次项存在，故其决策面为：

logP(C1|x)P(C2|x)=logf1(x)f2(x)+logπ1π2=xT(Σ−11−Σ−12)x+xTΣ−1(μ1−μ2)−12(μ1+μ2)TΣ−1(μ1−μ2)+logπ1π2−12log|Σ1||Σ2|

其对应的判别函数为：

δk(x)=−12(x−μk)TΣ−1(x−μk)−12log|Σk|+logπk

下面这份代码是LDA和QDA的测试代码：

# -*- coding: utf-8 -*-

"""
@author: duanxxnj@163.com
@time: 2015-07-09_16-01

线性判别式分析示例代码

"""

print __doc__

import numpy as np

import matplotlib.pyplot as plt
from matplotlib import colors

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis

##########################################################
# 颜色设置
cmap = colors.LinearSegmentedColormap(
'red_blue_classes',
{
'red': [(0, 1, 1), (1, 0.7, 0.7)],
'green': [(0, 0.7, 0.7), (1, 0.7, 0.7)],
'blue': [(0, 0.7, 0.7), (1, 1, 1)]
}
)

plt.cm.register_cmap(cmap=cmap)

###########################################################
# 生成数据
def dataset_fixed_cov():
'''产生两个拥有相同方差的高斯样本集合'''
n, dim = 300, 2 # 样本数目为300，特征维度为2
np.random.seed(0)
c = np.array([[0, -0.23], [0.83, 0.23]]) #高斯分布的方差
X = np.r_[np.dot(np.random.randn(n, dim), c),
np.dot(np.random.randn(n, dim), c) + np.array([1, 1])]
y = np.hstack((np.zeros(n), np.ones(n)))
return X, y

def dataset_cov():
'''产生两个拥有不同的方差的高斯样本集合'''
n, dim = 300, 2
np.random.seed(0)
c = np.array([[0.1, -1.0], [2.5, 0.7]]) * 2.0
X = np.r_[np.dot(np.random.randn(n, dim), c),
np.dot(np.random.randn(n, dim), c.T) + np.array([1, 4])]
y = np.hstack((np.zeros(n), np.ones(n)))
return X, y

#########################################################################
# 绘图函数
def plot_data(lda, X, y, y_pred, fig_index):
splot = plt.subplot(2, 2, fig_index)
if fig_index == 1:
plt.title('Linear Discriminant Analysis')
plt.ylabel('Data with fixed covariance')
elif fig_index == 2:
plt.title('Quadratic Discriminant Analysis')
elif fig_index == 3:
plt.ylabel('Data with varying covariances')

tp = (y == y_pred) #正样本中，分类正确的数目
tp0, tp1 = tp[y == 0], tp[y == 1]
X0 , X1 = X[y == 0], X[y == 1]
X0_tp, X0_fp = X0[tp0], X0[~tp0]
X1_tp, X1_fp = X1[tp1], X1[~tp1]

# 类别0分类正确的点和分类错误的点
plt.plot(X0_tp[:, 0], X0_tp[:, 1], 'o', color='red')
plt.plot(X0_fp[:, 0], X0_fp[:, 1], '.', color='#990000')

# 类别1分类正确的点和分类错误的点
plt.plot(X1_tp[:, 0], X1_tp[:, 1], 'o', color='blue')
plt.plot(X1_fp[:, 0], X1_fp[:, 1], '.', color='#000099')

# 类别0和类别1的区域
nx, ny = 200, 100
x_min, x_max = plt.xlim()
y_min, y_max = plt.ylim()
xx, yy = np.meshgrid(np.linspace(x_min, x_max, nx),
np.linspace(y_min, y_max, ny))
# 求出LDA的概率分布
z = lda.predict_proba(np.c_[xx.ravel(), yy.ravel()])
z = z[:, 1].reshape(xx.shape)
plt.pcolormesh(xx, yy, z,
cmap='red_blue_classes',
norm=colors.Normalize(0., 1.))
# 这里的等高线，就是对应的决策面
# LDA的决策面是直线，而QDA的决策面是二次曲线
# 注意图中右下角那张图，途中的决策面是双曲线
# 为了更清楚的看出其为双曲线，可以去掉后面两行代码的注释
plt.contour(xx, yy, z, [0.5], linewidths=2., colors='k')
#plt.contour(xx, yy, z, [0.4, 0.6], linewidths=2., colors='g')
#plt.contour(xx, yy, z, [0.3, 0.7], linewidths=2., colors='b')

# 类别0和类别1的中心点
plt.plot(lda.means_[0][0], lda.means_[0][1],
'o', color='k', markersize=10)
plt.plot(lda.means_[1][0], lda.means_[1][2],
'o', color='k', markersize=10)

for i, (X, y) in enumerate([dataset_fixed_cov(), dataset_cov()]):
print i
# 线性判别式分析
lda = LinearDiscriminantAnalysis(solver='svd', store_covariance=True)
y_pred = lda.fit(X, y).predict(X)
splot = plot_data(lda, X, y, y_pred, fig_index=2 * i + 1)
plt.axis('tight')

# 二次判别分析
qda = QuadraticDiscriminantAnalysis(store_covariances=True)
y_pred = qda.fit(X, y).predict(X)
splot = plot_data(qda, X, y, y_pred, fig_index= 2 * i + 2)
plt.axis('tight')

plt.show()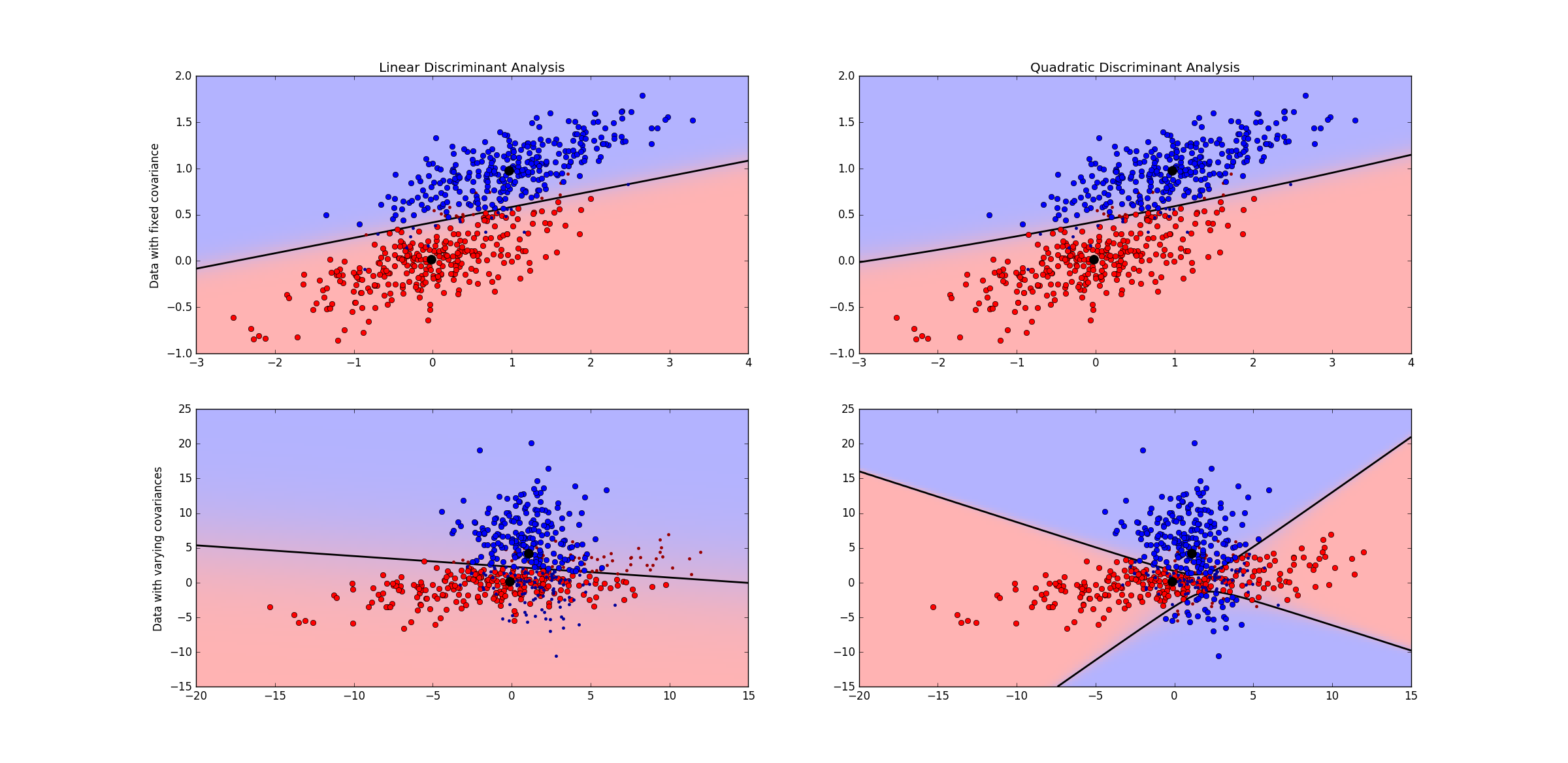

上面两幅图的数据是均值不同，方差相同的数据分布，LDA和QDA都得到一个线性的决策面。下面两幅图是均值和方差都不一样的数据分布，LDA得到一个线性决策面，但是QDA得到的决策面试一个双曲面，注意这里是一个双曲面，并不是两条直线。为了更好的看出其为双曲面，可以将代码中有两行等高线的代码注释去掉，就可以清晰的看出其决策面是双曲线了。

Fisher判别式

上面从贝叶斯公式出发，得到了线性判别分析的公式，这里从另外一个角度来看线性判别分析，也就是常说的Fisher判别式。其实Fisher判别式就是线性判别分析（LDA），只是在讨论Fisher判别式的时候，更侧重于LDA的数据降维的能力。

在应用统计学方法解决模式识别、机器学习中的问题的时候，有一个问题总是会出现：维数问题。很多在低维空间里可以解析或者计算的算法，在高维空间里面往往行不通，因此，数据降维就成了处理实际问题中的关键。

单纯的从数学角度考虑，将d维空间的数据压缩称为1维的数据是非常的容易的。然而，即便样本集合在d维空间里形成若干紧凑的相互分得开的集合，当把它们投影到某一个直线上的时候，就可能使得这些样本混合在一起无法分别开来。但，在实践中发现，总可以找到某个方向，使得在这个方向的直线上，样本的投影能分开的最好。那么，现在的问题就是，如何根据实际情况找到这条最好的、最容易分类的投影线。这就是线性判别分析（Linear Discriminant Analysis）所要解决的基本问题，线性判别分析在很多时候，也叫做 Fisher’s linear discriminant（Fisher线性判别式）。准确的说，它是在Fisher线性判别式基础上的一个推广。

线性判别分析的基本思想，是将高维的模式样本投影到最佳鉴别矢量空间，以达到抽取分类信息和压缩特征空间维数的效果，投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离，即模式在该空间中有最佳的可分离性，因此，它是一种有效的特征抽取方法。

在上面关于线性判别分析的说明中提到，投影后的样本在新的空间需要有最大的类间距离和最小的类内距离。那么，什么是类间距离？什么又是类内距离？线性判别分析又是如何在最大化类间距离的同时最小化类内距离？回答完了这三个问题，就基本上能对线性判别分析有一个基本的了解了。

类间距离

对于线性分类器，有一种观点就是将线性分类器看成是一个降维的操作。这里首先考虑二分类的问题，假设输入向量x是D维的，并使用下面这个变换，将x投影到一个一维的数据y上：

y=wTx

此时在y上加一个阈值−w0，并以此来做二分类：

{C1C2y≥−w0y<−w0

毫无疑问，上面的这种投影操作，会损失大量的样本信息，同时在投影的直线上，可能会使得各个类别的数据相互重叠，无法分别开来。但无论怎样，通过调整w都可以找到一条最好的直线，使得投影之后类之间的距离能够最大。

每一类的数据都像是一个云团，存在各自的分布，那么如何定义两个类之间的距离呢？这里可以先考虑两个类C1,C2各自的均值m1,m2：

m1=1N1∑x∈C1,m2=1N2∑x∈C2

用两个均值m1,m2之间的距离m1−m2，作为类之间的距离，这是一种非常简单直观的类间距离的定义方法。

当两个类分别通过w做投影之后，那么投影之后的类间距离为：

m˜1−m˜2=wT(m1−m2)

这里m˜1 是C1投影之后的类均值；m˜2 是C2投影之后的类均值。而我们要做的，就是要找一个w能够最大化m˜1−m˜2。但是，从上面的式子可以看出，通过增大w的模，可以无限的增大m˜1−m˜2，为了解决这个问题，需要将w的模设为1：||w||2=1。也即是说，w的模并不重要，重要的是w的方向。

对上面的式子，使用拉格朗日乘子法：

wT(m1−m2)+λ(wTw−1)

对w求导之后，得到：

(m1−m2)+λw=0⇒w∝(m1−m2)

这个结果也是显然的，使用类的均值作为类间距离，要在投影的时候最大化类间距离，自然要让投影线和(m1−m2)平行。

但是，单纯最大化类间距离真的就可以让投影后类之间的重叠最少吗？看下面这幅图。这幅图是从PRML上截取下来的，这幅图左边就是单纯的最大化类间距离，所以左图中w和(m1−m2)是平行的。右图是Fisher线性判别式(Fisher linear discriminant)得到的w。



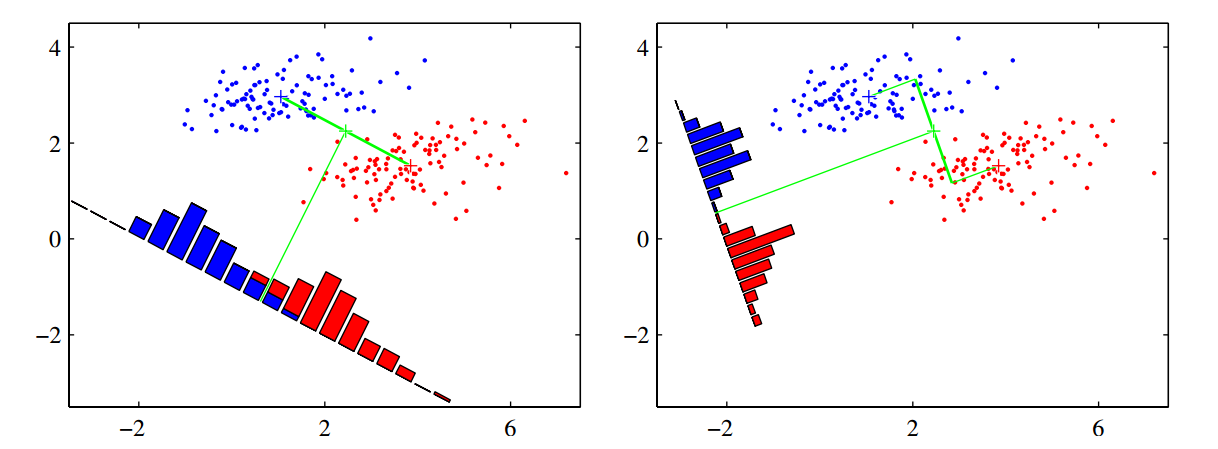
很显然相对于右图而言，单纯的最大化类间距离无法让投影后类的重叠最小，那么Fisher线性判别式到底又做了什么才能到到这个效果呢？这就是下面要讲的：最小化类内距离。

类内距离

对于一个存在一定的分布的类而言，我们用来定义这个类的类内距离，最常用的，就是方差（variance），方差所表示的，就是数据的离散程度。一个类Ck在w上投影之后，其类内方差为：

s˜2k=∑n∈Ck(yn−m˜k)2

这里 yn=wTxn ，是xn在w上的投影。

在很多网上的博客以及中文的教材中，讨论到类内距离的时候，都是说这个是类的散度矩阵，其实这个就是数据的方差，用散度矩阵这个名字，只是为了让这个理论显得特别的高深的感觉，千万不用被忽悠了。

我们可以定义，投影后，总的类内方差为：投影后，各自类内方差的总和：s˜21+s˜22。

Fisher线性判别式

上面已经介绍了类间距离，也就是类的均值的差；类内距离，也就是类内的方差。Fisher线性判别式的基本思想就是要最大化类间距离，同时最小化类内距离。这里就定义一个比值：

J(w)=(m˜1−m˜2)2s˜21+s˜22

将这个比值最大化，就可以达到最大化类间距离的同时，最小化类内距离了。

对于原始的数据而言，其类内方差可以写为：

s2k=∑n∈Ck(yn−mk)2=∑x∈Ck(x−mk)(x−mk)T

投影后的类内方差为：

s˜2k=∑n∈Ck(yn−m˜k)2=∑x∈Ck(wTx−wTmk)(wTx−wTmk)T=∑x∈Ck(wT(x−mk)(x−mk)Tw)=wTs2kw

这里定义原始数据的类内总方差为:

Sw=s21+s22

那么投影后的类内总方差为：

s˜21+s˜22=wT(s21+s22)w=wTSww

投影后，类间距离也可以写成相似的形式：

(m˜1−m˜2)2=(wTm1−wTm2)2=wT(m1−m2)(m1−m2)Tw

这里定义：

Sb=(m1−m2)(m1−m2)T

那么，投影后的类间距离可以写成为：

(m˜1−m˜2)2=(wTm1−wTm2)2=wT(m1−m2)(m1−m2)Tw=wTSbw

这样，就是可以把Fisher判别式的判别准则重写为下面这个形式：

J(w)=(m˜1−m˜2)2s˜21+s˜22=wTSbwwTSww

其中：

Sb=(m1−m2)(m1−m2)T

Sw=∑x∈C1(x−m1)(x−m1)T+∑x∈C2(x−m2)(x−m2)T

上面这个式子对w求导之后，可以得到：

w=S−1w(m1−m2)

这样，我们就可以得到将投影后的类间距离最大化，同时投影后的类内距离最小化的之间w。这样，就从一个D维问题转化为了一个更容易分析和处理的一维问题。

当然，这个问题是一个多对一的问题，从理论上讲，在很多训练样本的情况下，这个方法不仅不能让最小误差率降低，甚至会在一定程度上提高误差率。然而，我们总还是愿意为了得到在一维中操作的方便性，而想要的牺牲一些理论上的分类效果。

此时，最后剩下的问题就是如何在投影后，求解阈值，来进行分类了。阈值点，就是在一维空间中，可以将两类分开的那个点的位置，这个问题相对来说非常的简单，这里不予讨论。

这里有一种特殊情况，就是当数据的条件概率分布函数p(x|Ck)是多远正太函数，并且各个类别的协方差矩阵Σ相同的时候，最佳的判别边界方程为：

wTx+w0=0

其中：

w=Σ−1(μ1−μ2)

计算Fisher判别准则下最佳的w的计算复杂度主要是计算Sw，和它的逆，所带来的，所以其复杂度为O(D2n)

从上面的推导可以看出，Fisher判别式就是线性判别分析（LDA），只是在讨论Fisher判别式的时候，更侧重于LDA的数据降维的能力。

# -*- coding: utf-8 -*-

"""
@author: duanxxnj@163.com
@time: 2015-07-11_16-17

线性判别式分析数据降维示例

"""

print __doc__

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

# 读取iris数据，
# 这个数据的特征维度为4维
# 样本的类别有三中
iris = datasets.load_iris()

X = iris.data
y = iris.target
target_names = iris.target_names

# 将数据的特征维度降为一维
# 当然这里可以将n_components设置为任何小于原始特征维度的数目
lda = LinearDiscriminantAnalysis(n_components=1)
X_r2 = lda.fit(X, y).transform(X)
X_Zreo = np.zeros(X_r2.shape)

for c ,i , target_names in zip('ryb', [0, 1, 2], target_names):
plt.scatter(X_r2[y == i], X_Zreo[y == i], c=c, label=target_names)

plt.grid()
plt.legend()
plt.show()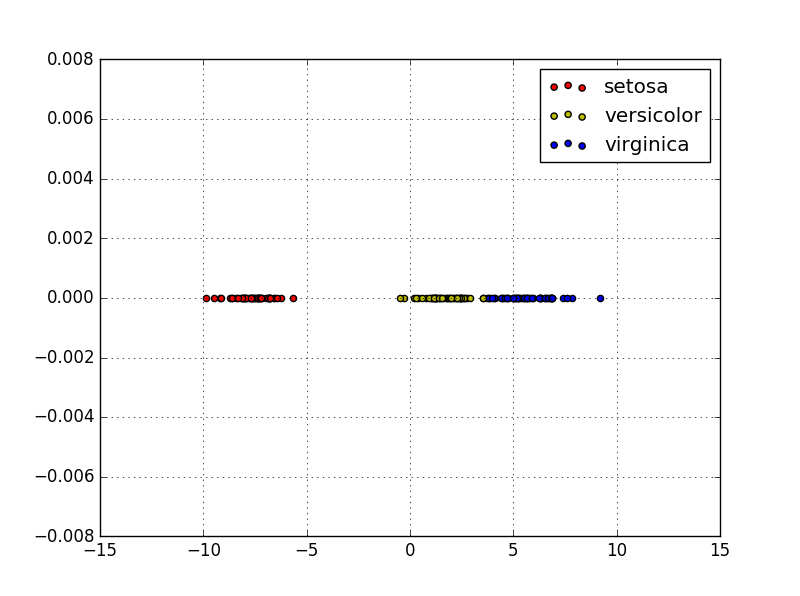

这里是将iris数据集的4维特征，转换成了一维的特征，可以看出，转换之后的特征任然有很强的分类能力，这就是LDA的数据降维能力。