线性代数中向量、矩阵深度理解（PartI）

本文参考资料：Introduction to linear algebra (Gilbert Strang)书以及其在MIT的视频。

看了有一周了，矩阵的认识不限于本科所学的固定运算，知道从空间中去理解，这对于后续子空间、各种空间变换学习来说很关键。故总结于此。

目录：

向量理解（线性组合）

矩阵理解（Ax=b中从row picture及column picture的理解）

矩阵乘法理解（四种方式）

Gauss-Jordan 消元法

A=LU分解

矩阵相关性质

1.向量理解

一般提及向量，都是指列向量（一条长长的彩带），有方向（thea）有长度（模）。最需要理解的概念是线性组合（linear combination）。

线性组合定义：cv+dw是向量v与向量w的线性组合；

能线性组合的前提：向量v和w维数相等。组合后的向量在空间中所占的位置：

1）对于一个向量u，线性组合cu是一条线；

2）对于二个向量u和w，线性组合cu+dw张满一个平面；

3）对于三个向量u，v和w，线性组合cu+dv+ew填满一个三维空间；

2.矩阵理解

从（1）线性组合衍生到矩阵乘法；（2）从解n个未知数n个线性方程的线性方程组理解；

(1)


重写线性组合更便于理解矩阵的乘法。开始，数值c，d，e乘以向量。现在变成矩阵乘以这些数值。Ax=对矩阵列向量的线性组合。

(2)


以上的线性方程组可以简化成Ax=b，问题：是否对任意的b，方程组均有解？

=> 列的线性组合能否覆盖整个二维空间？

答案很明显，不是。如：如果列向量之间线性相关，那么其线性组合只能覆盖一条直线，在这种情况下，只有当b在这条直线上才会有解（无数多个解），否则没有解。

当矩阵A是非奇异矩阵（non-sigular matrix）且可逆（invertible）时方程组对任意b有解。

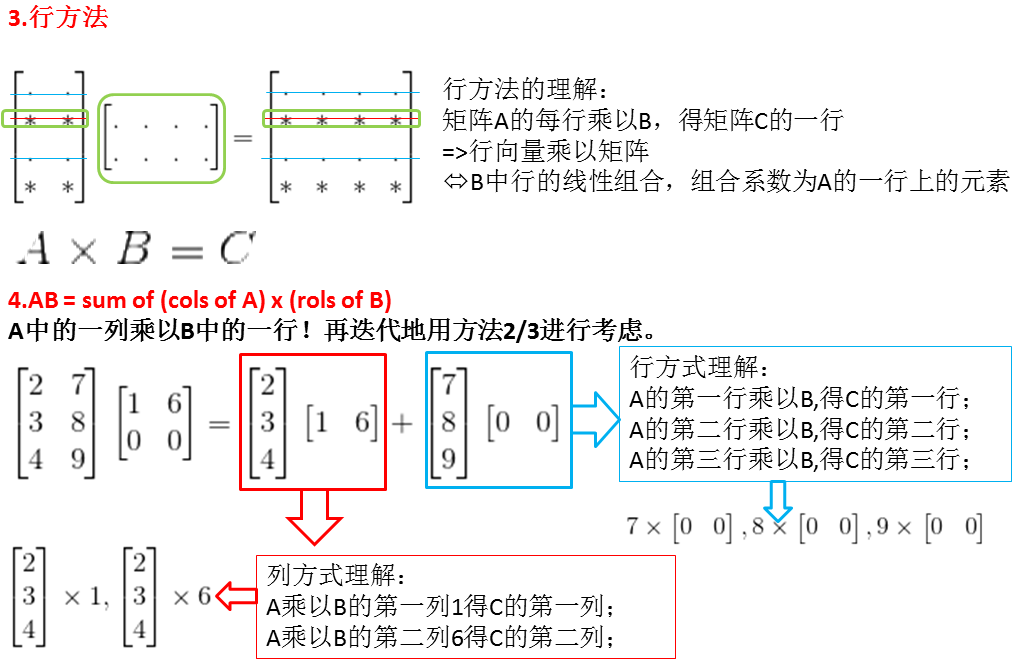
3.矩阵乘法（四种理解方式）



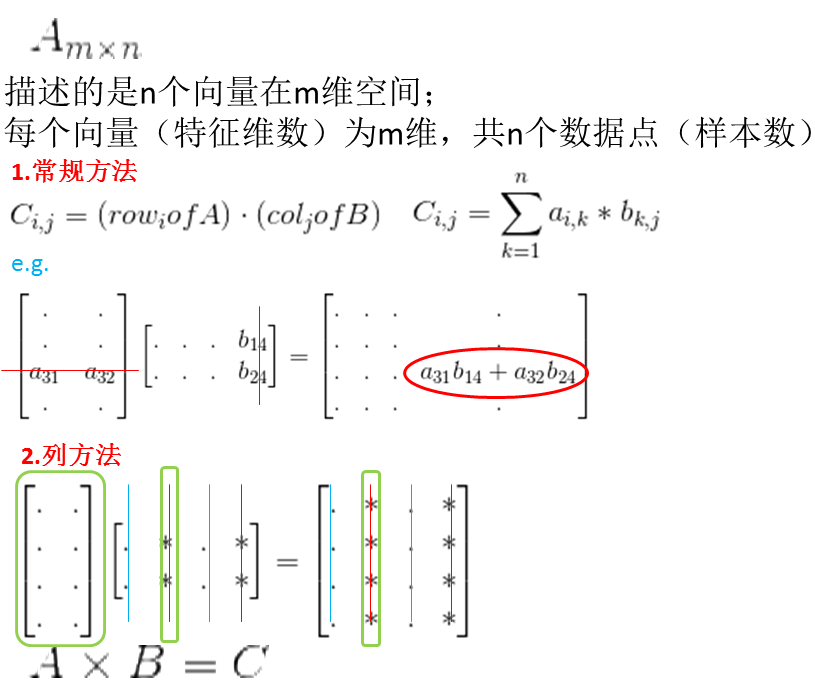
列乘法的理解：矩阵A依次乘以矩阵B的很多列=>矩阵乘向量<=>（理解）矩阵A的列的线性组合，组合的系数就是B上一列的元素。



Gauss-Jordan 消元法

A=LU分解

矩阵相关性质

这三个章节在后续文章中讲述。