《用 Python 学微积分》笔记 1
2016-04-21 22:09
639 查看
《用 Python 学微积分》原文见参考资料 1。
1、多项式
f(x)=x3-5x2+9
View Code
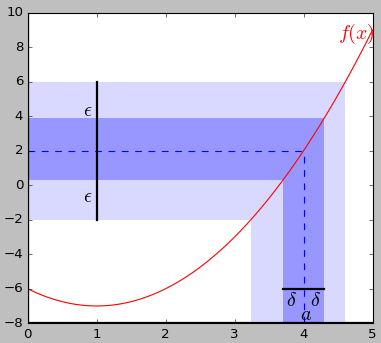
现在用上面的定义来证明:
$$\lim_{x\rightarrow 4}x^2-2x-6=2$$
即对于任意的 ε>0,能找到一个 δ>0,使得 0<|x-4|<δ 时,有 |f(x)-2|<ε。
证明:注意到 |f(x)-2|=|x2-2x-6-2|=|(x-4)(x+2)|=|x-4|·|x+2|,已知 |x-4|<δ,根据三角形不等式,|x+2|=|x-4+6|≤|x-4|+6<δ+6,所以
|f(x)-2|=|x-4|·|x+2|<δ·(δ+6),现在只需找到一个 δ,满足 δ·(δ+6)<ε 即可,用二元一次方程知识就可以证明这样的 δ>0 是存在的。
或者只要令 δ=min(1,ε/7),即可使得 δ≤ε/7 且 δ+6≤7,使得 δ·(δ+6)<ε。
11、泰勒级数用于极限计算
我们在中学课本中一定记忆了常见的极限,以及极限计算的规则,这里我们便不再赘言。泰勒级数也可以用于计算一些形式比较复杂的函数的极限。这里,仅举一例:
$$\lim_{x\rightarrow 0}\frac{sin(x)}{x}=\lim_{x\rightarrow 0}{\frac{\frac{x}{1!}-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\dots}{x}}$$
$$\qquad = \lim_{x\rightarrow 0}{\frac{x(1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}+\dots)}{x}}$$
$$\qquad = \lim_{x\rightarrow 0}{1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}+\dots}$$
$$\qquad = 1$$
12、洛必达法则
利用泰勒级数来计算极限,有时也会陷入困境,例如:求极限的位置是在我们不知道泰勒展开的位置,或者所求极限是无穷的。通常遇到这些情况我们会使用各种形式的洛必达法则。
这里我们仅尝试说明
$$\frac{0}{0}$$
形式的洛必达法则为何成立。
如果 f 和 g 是连续函数,且
$$\lim_{x\rightarrow a}f(x)=0,\quad \lim_{x\rightarrow a}g(x)=0$$
若
$$\lim_{x\rightarrow a}\frac{f'(x)}{g'(x)}$$
存在,则:
$$\lim_{x\rightarrow a}\frac{f(x)}{g(x)}=\lim_{x\rightarrow a}\frac{f'(x)}{g'(x)}$$
如果分子分母求导后仍然是 0/0 形式,那么重复该过程,直至问题解决。
运用泰勒级数,我们很容易可以理解洛必达法则为什么会成立:
$$\lim_{x\rightarrow a}{\frac{f(x)}{g(x)}}=\lim_{x\rightarrow a}{\frac{f(a)+\frac{f'(a)}{1!}(x-a)+\frac{f''(a)}{2!}(x-a)^2+\frac{f'''(a)}{3!}(x-a)^3+\dots}{g(a)+\frac{g'(a)}{1!}(x-a)+\frac{g''(a)}{2!}(x-a)^2+\frac{g'''(a)}{3!}(x-a)^3+\dots}}$$
$$\qquad = \lim_{x\rightarrow a}{\frac{\frac{f'(a)}{1!}(x-a)+\frac{f''(a)}{2!}(x-a)^2+\frac{f'''(a)}{3!}(x-a)^3+\dots}{\frac{g'(a)}{1!}(x-a)+\frac{g''(a)}{2!}(x-a)^2+\frac{g'''(a)}{3!}(x-a)^3+\dots}}$$
$$\qquad =\lim_{x\rightarrow a}{\frac{f'(a)+\frac{f''(a)}{2!}(x-a)+\frac{f'''(a)}{3!}(x-a)^2+\dots}{g'(a)+\frac{g''(a)}{2!}(x-a)+\frac{g'''(a)}{3!}(x-a)^2+\dots}}$$
$$\qquad = \lim_{x\rightarrow a}\frac{f'(x)}{g'(x)}$$
参考资料:
[1] https://ryancheunggit.gitbooks.io/calculus-with-python/content/
1、多项式
f(x)=x3-5x2+9
import numpy as np
import sympy
import matplotlib.pyplot as plt
f = lambda x: x**2-2*x-6
x = np.linspace(0,5,100)
y = f(x)
plt.plot(x,y,'red')
plt.grid('off')
l = plt.axhline(-8,0,1,linewidth = 2, color = 'black')
l = plt.axvline(0,0,1,linewidth = 2, color = 'black')
l = plt.axhline(y=2,xmin=0,xmax=0.8,linestyle="--")
l = plt.axvline(x=4,ymin=0,ymax=float(5)/9, linestyle = "--")
l = plt.axhline(-6,3.7/5,4.3/5,linewidth = 2, color = 'black')
l = plt.axvline(1,6.0/18,14.0/18,linewidth = 2, color = 'black')
p = plt.axhspan(-2,6,0,(1+np.sqrt(13))/5,alpha = 0.15, ec = 'none')
p = plt.axvspan((1+np.sqrt(5)),(1+np.sqrt(13)),0,1.0/3,alpha = 0.15, ec = 'none')
p = plt.axhspan(f(3.7),f(4.3),0,4.3/5,alpha = 0.3, ec = 'none')
p = plt.axvspan(3.7,4.3,0,(f(3.7)+8)/18,alpha = 0.3, ec = 'none')
plt.axis([0,5,-8,10])
plt.text(0.8,-1,r"$\epsilon$", fontsize = 18)
plt.text(0.8,4,r"$\epsilon$", fontsize = 18)
plt.text(3.75,-7.0,r"$\delta$", fontsize = 18)
plt.text(4.1,-7.0,r"$\delta$", fontsize = 18)
plt.text(3.95,-7.8,r"$a$", fontsize = 18)
plt.text(4.5,8.5,r"$f(x)$", fontsize = 18,color="red")
plt.show()View Code

现在用上面的定义来证明:
$$\lim_{x\rightarrow 4}x^2-2x-6=2$$
即对于任意的 ε>0,能找到一个 δ>0,使得 0<|x-4|<δ 时,有 |f(x)-2|<ε。
证明:注意到 |f(x)-2|=|x2-2x-6-2|=|(x-4)(x+2)|=|x-4|·|x+2|,已知 |x-4|<δ,根据三角形不等式,|x+2|=|x-4+6|≤|x-4|+6<δ+6,所以
|f(x)-2|=|x-4|·|x+2|<δ·(δ+6),现在只需找到一个 δ,满足 δ·(δ+6)<ε 即可,用二元一次方程知识就可以证明这样的 δ>0 是存在的。
或者只要令 δ=min(1,ε/7),即可使得 δ≤ε/7 且 δ+6≤7,使得 δ·(δ+6)<ε。
11、泰勒级数用于极限计算
我们在中学课本中一定记忆了常见的极限,以及极限计算的规则,这里我们便不再赘言。泰勒级数也可以用于计算一些形式比较复杂的函数的极限。这里,仅举一例:
$$\lim_{x\rightarrow 0}\frac{sin(x)}{x}=\lim_{x\rightarrow 0}{\frac{\frac{x}{1!}-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\dots}{x}}$$
$$\qquad = \lim_{x\rightarrow 0}{\frac{x(1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}+\dots)}{x}}$$
$$\qquad = \lim_{x\rightarrow 0}{1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}+\dots}$$
$$\qquad = 1$$
12、洛必达法则
利用泰勒级数来计算极限,有时也会陷入困境,例如:求极限的位置是在我们不知道泰勒展开的位置,或者所求极限是无穷的。通常遇到这些情况我们会使用各种形式的洛必达法则。
这里我们仅尝试说明
$$\frac{0}{0}$$
形式的洛必达法则为何成立。
如果 f 和 g 是连续函数,且
$$\lim_{x\rightarrow a}f(x)=0,\quad \lim_{x\rightarrow a}g(x)=0$$
若
$$\lim_{x\rightarrow a}\frac{f'(x)}{g'(x)}$$
存在,则:
$$\lim_{x\rightarrow a}\frac{f(x)}{g(x)}=\lim_{x\rightarrow a}\frac{f'(x)}{g'(x)}$$
如果分子分母求导后仍然是 0/0 形式,那么重复该过程,直至问题解决。
运用泰勒级数,我们很容易可以理解洛必达法则为什么会成立:
$$\lim_{x\rightarrow a}{\frac{f(x)}{g(x)}}=\lim_{x\rightarrow a}{\frac{f(a)+\frac{f'(a)}{1!}(x-a)+\frac{f''(a)}{2!}(x-a)^2+\frac{f'''(a)}{3!}(x-a)^3+\dots}{g(a)+\frac{g'(a)}{1!}(x-a)+\frac{g''(a)}{2!}(x-a)^2+\frac{g'''(a)}{3!}(x-a)^3+\dots}}$$
$$\qquad = \lim_{x\rightarrow a}{\frac{\frac{f'(a)}{1!}(x-a)+\frac{f''(a)}{2!}(x-a)^2+\frac{f'''(a)}{3!}(x-a)^3+\dots}{\frac{g'(a)}{1!}(x-a)+\frac{g''(a)}{2!}(x-a)^2+\frac{g'''(a)}{3!}(x-a)^3+\dots}}$$
$$\qquad =\lim_{x\rightarrow a}{\frac{f'(a)+\frac{f''(a)}{2!}(x-a)+\frac{f'''(a)}{3!}(x-a)^2+\dots}{g'(a)+\frac{g''(a)}{2!}(x-a)+\frac{g'''(a)}{3!}(x-a)^2+\dots}}$$
$$\qquad = \lim_{x\rightarrow a}\frac{f'(x)}{g'(x)}$$
参考资料:
[1] https://ryancheunggit.gitbooks.io/calculus-with-python/content/
相关文章推荐
- Python模块——学习笔记
- Python函数式编程——学习笔记
- Python多线程互斥锁
- Python高级特性——学习笔记
- cmd命令行交互执行python引入模块时提示ImportError: No module named xxx
- Python函数——学习笔记
- python语言的解释性执行问题(备份一下,以供以后学习参考)
- Python框架之Tornado(四)源码之褪去模板外衣
- 菜鸟入门_Python_机器学习(4)_PCA和MDA降维和聚类
- Python框架之Tornado(四)源码之褪去模板外衣的前戏
- Python框架之Tornado(四)源码之褪去模板外衣的前戏
- Python语言快速入门
- Python框架之Tornado(二)请求阶段
- 菜鸟入门_Python_机器学习(3)_回归
- 安装Python及后续
- Python框架之Tornado(一)
- Python框架之Tornado(一)
- Python之Web框架
- Python 装饰器(进阶篇)
- Python 装饰器(进阶篇)
