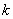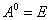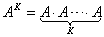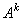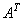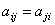您的位置：首页 > 其它

图像处理的坐标变换必备的矩阵知识

2016-04-21 20:44 288 查看

6.5 矩阵的运算及其运算规则

一、矩阵的加法与减法

　　1、运算规则

　　设矩阵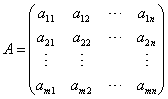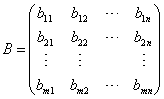

，

，

　　则

　　　　　


　　简言之，两个矩阵相加减，即它们相同位置的元素相加减！

　　注意：只有对于两个行数、列数分别相等的矩阵（即同型矩阵），加减法运算才有意义，即加减运算是可行的．

　　2、 运算性质 （假设运算都是可行的）

　　满足交换律和结合律

　　交换律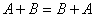　

；

　　结合律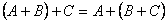　

．

二、矩阵与数的乘法

　　1、 运算规则

　　数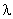

乘矩阵A，就是将数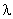

乘矩阵A中的每一个元素，记为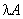

或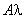

．

　　特别地，称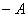

称为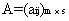

的负矩阵．

　　2、 运算性质

　　满足结合律和分配律

　　结合律： (λμ)A=λ(μA) ； (λ+μ)A =λA+μA．

　　分配律： λ (A+B)=λA+λB．

　　典型例题

　　例6.5.1　已知两个矩阵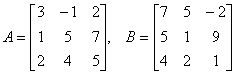



　　满足矩阵方程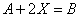

，求未知矩阵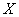

．

　　解　由已知条件知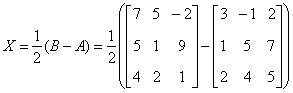

　 　


　　　　


三、矩阵与矩阵的乘法

　　1、 运算规则

　　设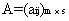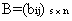

，

，则A与B的乘积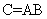

是这样一个矩阵：

　　(1) 行数与（左矩阵）A相同，列数与（右矩阵）B相同，即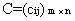

．

　　(2) C的第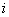

行第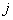

列的元素

由A的第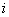

行元素与B的第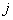

列元素对应相乘，再取乘积之和．

　　典型例题

　　例6.5.2　设矩阵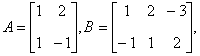



　　计算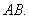


　　解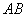　

是

的矩阵．设它为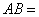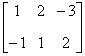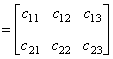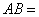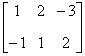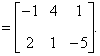

　　　　








　　　　








　　想一想：设列矩阵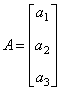

，行矩阵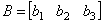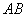

，

和

的行数和列数分别是多少呢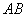


　　

是3×3的矩阵，

是1×1的矩阵，即

只有一个元素．

　　课堂练习

　　1、设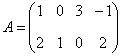

，

，求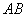

．

　　2、在第1道练习题中，两个矩阵相乘的顺序是A在左边，B在右边，称为A左乘B或B右乘A．如果交换顺序，让B在左边，A在右边，即A右乘B，运算还能进行吗？请算算试试看．并由此思考：两个矩阵应当满足什么条件，才能够做乘法运算．

　　3、设列矩阵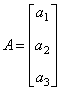

，行矩阵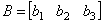

，求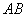

和

，比较两个计算结果，能得出什么结论吗？

　　4、设三阶方阵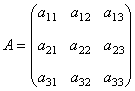

，三阶单位阵为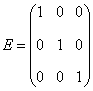

，试求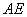

和

，并将计算结果与A比较，看有什么样的结论．

　　解：

　　第1题


．
　　第2题

　　对于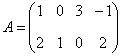


，

．
　　求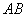

是有意义的，而

是无意义的．

　　结论1　只有在下列情况下，两个矩阵的乘法才有意义，或说乘法运算是可行的：左矩阵的列数＝右矩阵的行数．

　　第3题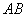

　　

是

矩阵，

是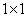

的矩阵．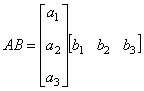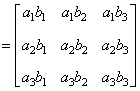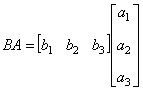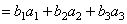

　　　



．





结论2　在矩阵的乘法中，必须注意相乘的顺序．即使在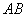

与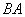

均有意义时，也未必有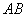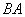

=

成立．可见矩阵乘法不满足交换律．

　　第4题

　　计算得：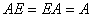

．

　　结论3　方阵A和它同阶的单位阵作乘积，结果仍为A，即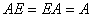

．

　　单位阵在矩阵乘法中的作用相当于数1在我们普通乘法中的作用．

　　典型例题

　　例6.5.3　设

，试计算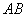

和

．

　　解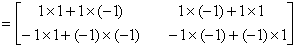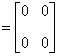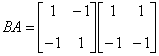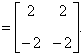　


　　　　　　


　　　　　　

．

　　　　


　　　　　　


　　　　　　


结论4　两个非零矩阵的乘积可以是零矩阵．由此若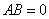

，不能得出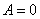

或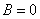

的结论．

　　例6.5.4　利用矩阵的乘法，三元线性方程组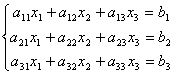



　　可以写成矩阵的形式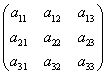




＝


　　若记系数、未知量和常数项构成的三个矩阵分别为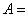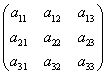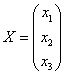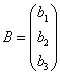




，

，

，
　　则线性方程组又可以简写为矩阵方程的形式：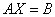

．

　　2、 运算性质（假设运算都是可行的）

　　(1)　结合律　

．

　　(2)　分配律　

（左分配律）；

　　　　　　　　　

（右分配律）．

　　(3)　

．

　　 3、 方阵的幂




定义：设A是方阵，

是一个正整数，规定


，


显然，记号

表示

个A的连乘积．



四、矩阵的转置

　　1、 定义



定义：将矩阵A的行换成同序号的列所得到的新矩阵称为矩阵A的转置矩阵，记作

或

．



　　例如，矩阵

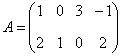的转置矩阵为

．

　　2、运算性质（假设运算都是可行的）

　　(1)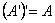　


　　(2)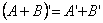　


　　(3)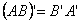　


　　(4)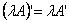　

，

是常数．

　　典型例题

　　例6.5.5 利用矩阵



　　验证运算性质：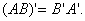


　　解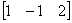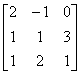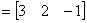　







；

　　而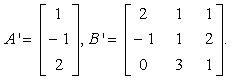

　　　　


　　所以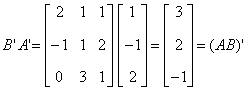

　　　

．




定义：如果方阵满足

，即

，则称A为对称矩阵．



　　对称矩阵的特点是：它的元素以主对角线为对称轴对应相等．

五、方阵的行列式

　　1、定义



定义：由方阵A的元素所构成的行列式（各元素的位置不变），称为方阵A的行列式，记作

或

．



　　2 、运算性质

　　(1)

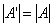（行列式的性质）

　　(2)

，特别地：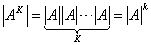


　　(3)

（

是常数，A的阶数为n）

　　思考：设A为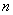

阶方阵，那么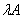

的行列式

与A的行列式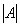

之间的关系为什么不是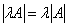

，而是

？
　　不妨自行设计一个二阶方阵，计算一下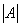

和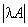

．

　　例如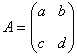

，则

．

　　于是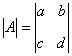

，而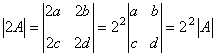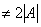



．

　　思考：设

，有几种方法可以求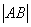

？

　　解 方法一：先求矩阵乘法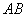

，得到一个二阶方阵，再求其行列式．

　　　　方法二：先分别求行列式

，再取它们的乘积．

3、逆矩阵

逆矩阵: 设A是数域上的一个n阶方阵，若在相同数域上存在另一个n阶矩阵B，使得: AB=BA=E。 则我们称B是A的逆矩阵，而A则被称为可逆矩阵。其用A^(-1)表示。

逆矩阵的性质为：

1 矩阵A可逆的充要条件是A的行列式不等于0。

2 可逆矩阵一定是方阵。

3 如果矩阵A是可逆的，A的逆矩阵是唯一的。

4 可逆矩阵也被称为非奇异矩阵、满秩矩阵。

5 两个可逆矩阵的乘积依然可逆。

6 可逆矩阵的转置矩阵也可逆。

7 矩阵可逆当且仅当它是满秩矩阵。

其中的方阵：就是行和列数相等的矩阵。

行列式：其就是求一个矩阵的数值，一般使用上三角或者下三角。其如下：



满秩矩阵：一个判断线性方程是否有解的关键条件，其是其说的就是要线性无关，其可分为列满秩和行满秩。其概念是：

满秩矩阵(non-singular matrix): 设A是n阶矩阵, 若r(A) = n, 则称A为满秩矩阵。但满秩不局限于n阶矩阵。若矩阵秩等于行数，称为行满秩;若矩阵秩等于列数，称为列满秩。既是行满秩又是列满秩则为n阶矩阵即n阶方阵。其中的R（A）指的就是求其秩。其中的行满秩就是行向量线性无关；列满秩就是列向量线性无关；其示意图如下：



3、 列（行）满秩阵与方程关系：



这也是为什么相机标定的时候每个视场只能提前四个有用的点，这时因为第五个点肯定跟前面的四个点其中一个线性相关，意思就是（x，y）（X,Y）这个肯定跟前面的一个点成倍数关系，这样子在求秩的时候，有成倍数的行会被化成零，则这就成了降秩了，就不是满秩了。

内容来自用户分享和网络整理，不保证内容的准确性，如有侵权内容，可联系管理员处理 点击这里给我发消息
标签： 
相关文章推荐
新的分享
章节导航