线段树详解

线段树简介：

　　　线段树是一种高效的数据结构，他的应用非常广泛，主要可以求区间和，求区间最小值，求区间最大值，求区间中某个数据出现的次数……为什么它效率这么高呢？因为它用到了二分的思想，将一个完整的线段的区间答案保存在根节点，左边是线段的左半部分，右边是线段的右半部分，以此类推。如下面就是一个线段树（求区间和）：

线段树的性质：

　　由上图，我们可以发现以下性质：1.一个由N个数据构成的线段树，其结点的数量为2N-1（不信你画）。

　　　　　　　　　　　　　　　　　2.一个由N个数据构成的线段树，其树的深度（以根节点深度为1算）为log2N（向上取整）+1（不信你画）。

　　　　　　　　　　　　　　　　　3.一个节点所管理的区间为L~R，那么它左孩子管理范围是L~(L+R)/2，右孩子是(L+R)/2+1~R（人家就这样定义

　　　　　　　　　　　　　　　　　的）

　　　　　　　　　　　　　　　　   4.每个线段树的叶子节点都是他的原有的数据（自己看图）。

　　　　　　　　　　　　　　　　　5.线段树是一个完全二叉树。

线段树的基本操作：

　　线段树的操作主要有三种：建树，查询，修改。其中修改又能细分为修改单个节点和{【修改整条线段】<-主要要讨论的内容}

线段树的建造：

　　首先我们都知道，树是递归定义的，那我们仔细观察观察上面那棵线段树，我们可以发现什么？ 没错，对一棵线段树按层序遍历编号：对于一个父亲节点而言，它的两个孩子节点之和就是它自己的值。我们可以推广这个结论，对一棵关于x操作的线段树，它的非叶子节点i的值等于他的孩子节点i*2和i*2+1通过x操作所得到的值，举个例子：设一个x操作为求区间最小值的线段树，它的第i*2节点的值为25，它的第i*2+1节点的值为28，那么第i个节点的值就是min(25,28) = 25;又比如上面那棵求和树，它的第二个节点的值（105）=它的第2*2=4个节点的值（45）+它的第2*2+1个节点的值（60）;

　　由性质5知，线段树是一个完全二叉树，那么我们就可以用数组来保存它（像保存堆那样）：

struct node{
int value;
}tree[10000 + 20];

　　这样，我们就不难写出建树操作了，下面以求和树为栗子：

void make_tree(int begin, int end, int pla){                 //构造线段树的过程，pla为当前处理数组的哪个位置
if(begin == end){      //叶子节点
tree[pla].value = a[begin];
return;
}else{                                                  //递归建树
make_tree(begin, (begin + end) / 2, pla * 2);
make_tree((begin + end) / 2 + 1, end, pla * 2 + 1);
}
tree[pla].value = tree[pla * 2].value + tree[pla * 2 + 1].value;   //求和
}

　　从上面这个代码我们可以看出，建树操作的复杂度是O(n)。

线段树的查找：

　　关于线段树的查找，各位应该看到树的样式就差不多明白了一些，比如上面那个求和树，查找1-7应该会吧，1-4应该也会吧，只要沿着树二分查找就行了。但是，看到这里各位肯定会产生到一丝疑惑，怎么查找不在这个线段树节点区间上的值，比如1-6,2-5,2-6？

　　我们不妨这样看：如下图，将1-6看成1-4和5-6，这样我们只需要进行两次查找，然后再进行一次那样的操作，就能得到答案了，比如上面那棵线段树，1-4为105,5-6为81，然后进行一次相加操作，得到答案186，不信你看图。

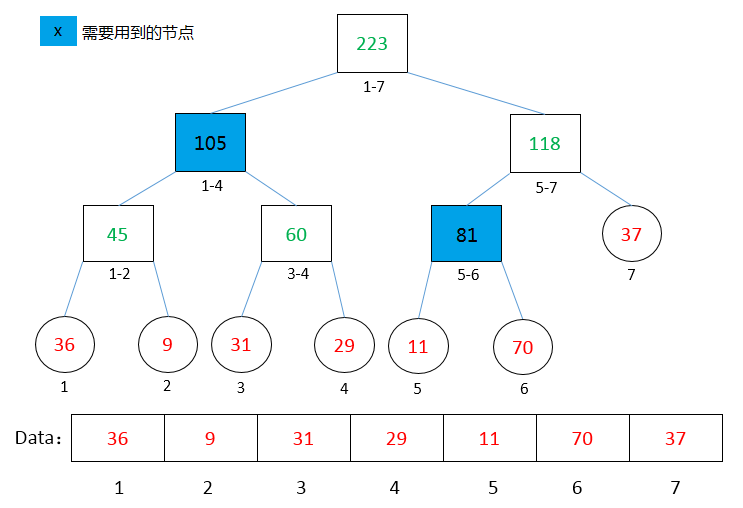
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （图：查找线段1-6）

　　以此类推，2-5可以看成2,3-4,5，根据上面那个二叉树，2为9,3-4为60,5为11，相加80，自己验证看看对不对。

　　2-6就略了，你们可以自己算算。

　　那么我们如何具体实现这个操作呢，我们不妨用集合的思想来想想：

当我们从根节点向下查找时，我们可以设计一个比较，比较当前要查找的这个节点begin~end和查找范围kaishi~jieshu的关系，我们设A={x | x在begin~end所代表的元素之间}，B={x | x在kaishi~jieshu所代表的元素之间}。如当begin=1，end=4时，A={36,9,31,29}，当kaishi=2，jieshu=5时，B={9,31,29,11}；

　　这样，我们就可以发现：当A∩B≠∅时，也就是说A这个范围内有我想要的东西，那我就进一步查找这个区间内的左右子树。

　　当A∩B=∅时，返回。

　　当A⊆B时，说明我们不需要进一步查找了，就可以存下来这个值，等到完成操作时再进行操作，当然我们也可以即时操作。

　　那么代码应该也不难写了，下面是查找操作的代码：

int sum = 0;
void lookup(int begin,int end,int kaishi,int jieshu,int pla){
if(jieshu < begin || kaishi > end)         //表示线段集合begin~end交线段集合kaishi~jieshu为空集合的情况
return;
else{
if(begin >= kaishi && end <= jieshu){    //线段集合begin~end子集于线段集合kaishi~jieshu
sum += tree[pla].value;
}else{                                   //交集不为空
lookup(begin, (begin + end) / 2, kaishi, jieshu , pla * 2);
lookup((begin + end) / 2 + 1, end, kaishi, jieshu, pla * 2 + 1);
}
}
}

由上面的代码，我们不难发现，当存在着一棵2N-1个节点的二叉树，最坏情况为查找2~N-1（自己去证）。那么它的时间复杂度为O(log2N);（你可以试着用笔画一下，会发现经过节点左右对称，数量大概是2log2N，所以是O(log2N)）;

线段树的修改操作：

　　线段树的修改分为两部分，一个是单个节点的修改，一个是线段的修改，相信大家看完线段树的查找后一定有了灵感，单个节点的修改肯定是没问题了。但是，如果按照单个节点的修改方法修改线段，假设线段长度为K，那么它的时间复杂度就是O(Klog2N)，这个效率是很差的，因为我们有方法可以使时间优化到O(log2N),这就要使用二叉树的最难的东西了——延迟标记;

　　那么我们要改一下代表线段树的数组的定义：

struct node{
int value;
int biaoji;
node(){biaoji = 0;}
}tree[10000 + 20];

　　延迟标记，顾名思义，就是延迟某项东西的处理时间，换句话说就是将一些事情拖到后面去做，到底是将什么拖到后面去做呢？既然是修改节点，那么肯定就是把修改节点的操作拖到后面去做。看到这里有些人就会疑惑了，既然是要修改线段，那么为什么不立即修改了呢，不修改那还叫什么修改线段呢？其实，我的意思是说不修改线段上的每一个具体的点，而是将树上某一些代表某条线段的节点给修改，然后存到延迟标记中，查找的时候消除掉它，应该说是下移。

　　说到这里肯定有人没理解，因为我也是看了好多次才懂的，举个实例吧，就给上面那棵线段树中1-4这一段每个节点增加3吧。这时，我们就先二分查找到代表1-4的2号节点，这时按照修改单个节点的方法就是继续向下查找，修改1,2,3,4，然后递归修改它们的父节点，这样的话效率就是O(4log27)，当要修改多个线段时这种时间复杂度是无法承受的，但我们引入延迟标记后，我们可以直接修改2号节点的值，并不向下继续修改1,2,3,4的值，然后更改2号节点的延迟标记增加3，意思是说1-4这个区间每个数我都欠了3给他们加。这时候肯定有人会问查找怎么办？我们仔细观察一下查找的步骤，都是由根往叶子查找的，而且查找没修改的点肯定会遇到被修改的那个点，比如说上面给1-4增加了3，那么我们要查找1-2的值时，必然会路过1-4，这时候延迟标记的作用又来了，我们将延迟标记向下移，将原先属于2号节点(1-4)的延迟标记送给它的两个孩子，即使它两个孩子的延迟标记增加3，然后给它的左右孩子的值增加(R-L+1)*3点。这样使得查找出来的结果正确，如果查找的范围不正好是节点所表示的区间的话，就用查找的方法二分。

　　代码如下：

void change(long long begin,long long end,long long kaishi,long long jieshu,long long pla,long long add) {
if(jieshu < begin || kaishi > end)
return;
else{
if(begin >= kaishi && end <= jieshu){
tree[pla].biaoji += add;
tree[pla].value += add * (end - begin + 1);
}else{
if(tree[pla].biaoji){
tree[pla * 2].biaoji += tree[pla].biaoji;
tree[pla * 2].value += ((begin + end) / 2 - begin + 1) * tree[pla].biaoji;
tree[pla * 2 + 1].biaoji += tree[pla].biaoji;
tree[pla * 2 + 1].value += (end - (begin+end) / 2 ) * tree[pla].biaoji;
tree[pla].biaoji=0;
}
change(begin, (begin + end) / 2, kaishi, jieshu , pla * 2,add);
change((begin + end) / 2 + 1, end, kaishi, jieshu, pla * 2 + 1,add);
if(begin!=end){
tree[pla].value = tree[pla*2].value + tree[pla*2+1].value;
}
}
}
}

反复读这个代码你就会知道到底延迟标记有什么用了。最坏情况O(log2n)，证明方法很简单，画张图就行了，画一张1~n的图，然后选择改变2~n-1，改变的是每层两个。一个二叉树有log2n层，所以复杂度为O(log2n)；

上面我们说过，查找的方式就是将延迟标记下移，这是坠吼的，所以我们要对查找进行一点PY交易。

long long sum = 0;
void lookup(long long begin,long long end,long long kaishi,long long jieshu,long long pla){
if(jieshu < begin || kaishi > end)
return;
else{
if(begin >= kaishi && end <= jieshu){
sum += tree[pla].value;
}else{
if(tree[pla].biaoji){
tree[pla * 2].biaoji += tree[pla].biaoji;
tree[pla * 2].value += ((begin + end) / 2 - begin + 1) * tree[pla].biaoji;
tree[pla * 2 + 1].biaoji += tree[pla].biaoji;
tree[pla * 2 + 1].value += (end - (begin+end) / 2 ) * tree[pla].biaoji;
tree[pla].biaoji=0;
}
lookup(begin, (begin + end) / 2, kaishi, jieshu , pla * 2);
lookup((begin + end) / 2 + 1, end, kaishi,jieshu, pla * 2 + 1);
}
}
}

进行完整棵肮脏的交易后，线段树就打完了，后面的两个延迟标记的我没测试，请看了的帮忙测试下，非常感谢！