dx11学习笔记-3.三维空间变换(自己整理,基础详尽)
2016-02-17 12:41
591 查看
三维空间变换其实是图形学的基本知识,和DX倒没有什么特定关系。但MS关于这块儿的文档教程解释得很详尽。看完之后我觉得我对于坐标变换的理解又深入了一步。此处我截取自己觉得精要的地方来说明。
译文:http://blog.csdn.net/zhanghua1816/article/details/23121735
2、http://dev.gameres.com/Program/Visual/3D/shenruTS.htm
3、http://blog.csdn.net/code_xbug/article/details/46299603
4、MS官方document-Tutorial04:3D Spaces
为什么图形学里要用到坐标空间变换呢?因为我们输入的模型顶点,通常都是定义在一个local space里的,也就是“局部坐标系”。这个坐标空间的特点就是,以模型上或者模型外一点为原点(通常在模型底心或中心),以正交的XYZ作为坐标轴(轴的方向定义通常与输入模型的面部朝向相关)。每一个输入的模型都有各自的Local space,当我们想把它在我们定义的世界空间里移动旋转缩放时,就面临着问题,因为我们执行的操作需要在一个统一的世界坐标系下执行。这时就需要用到坐标空间变换了——将一个局部坐标系下定义的顶点坐标,转换为世界坐标系下的顶点坐标。
图形学中共涉及以下几种坐标空间:
local space局部空间
world space世界空间
view space观察空间
projection space投影空间
screen space屏幕空间
将输入的模型最终显示到屏幕上,经过的空间变换也基本如上顺序所示。
那么,如何进行变换呢?
变换矩阵既然能联系两种坐标空间,那么其组成元素必定和坐标轴相关。事实上,从坐标空间A变换到空间B,需要知道A的三个坐标轴向量及原点坐标在B下的表示。而这四个信息(XYZ轴方向向量,原点坐标在新坐标系下的表示)就构成了变换矩阵。
DX中采用行主序,这和OPENGL的列主序相反。这意味着在DX和OPENGL中,向量与矩阵相乘的顺序恰好相反。此处既然是学DX,那就按照DX的规矩来。
我画了一张示意图如下:

这是两个坐标空间,红色是空间A,黑色是空间B,二者Y轴方向相反。假设空间A的原点Oa在空间B下的坐标表示为(1,1,1)。那么从A变换到B,矩阵应该这么表示:

第一行是Xa,第二行是Ya,第三行是Za,第四行是Oa。这就是变换矩阵的基本形式。
注意到我们把每一行最后一个数都补齐了,凑出了第四列。其实,三维坐标空间内任一点,我们也都会表示为(x,y,z,w)。这就是“齐次坐标”。
我们最常用的三维变换有平移、旋转、缩放。
先不考虑和矩阵相乘,单看点的坐标如何变换。
设有一点(x0,y0,z0)
平移平移向量为(dx,dy,dz),那么平移结果就是(x0+dz,y0+dy,z0+dz);
旋转由于三维空间的旋转需要分绕x轴、绕y轴、绕z轴的情况分别来看,为了方便讲解,所以我们这里不妨从二维空间的旋转入手。旋转需要用到极坐标的知识(需要满足:1、直角坐标系原点与极坐标极点重合;2、直角坐标系x轴正向轴与极坐标极轴重合。具体请查阅极坐标与直角坐标的转换)。设旋转角度为θ,那么旋转结果就是(x0*cosθ+y0*(-sinθ),x0*sinθ+y0*cosθ);
缩放这就简单多了,设缩放因子为(sx,sy,sz),那么缩放结果就是(x0*sx,y0*sy,z0*sz)。
可以看出,平移是与原坐标做加法,旋转缩放是与原坐标做乘法。那么如果把这两类运算都用矩阵和向量做乘法来表示,那么我们会发现,乘法还好说,而加法就有问题了。因为我们是用(x,y,z)来表示坐标的,根据向量和矩阵相乘的运算法则,我们最终只可能得到各向量分量点乘的结果,无法凭空得到一个常量加法因子。这时我们就不得不引入一个额外的常量w来执行加法,这就是齐次坐标(x,y,z,w)的作用。(当然运用齐次坐标不止这一个好处)
现在点的坐标已经用齐次坐标表示了,那矩阵(注意是行主序)用四行三列来表示,也没什么问题吧?为什么我们要用四行四列的矩阵来表示变换矩阵?其实很简单,行主序的矩阵运算中,m*n矩阵乘n*k矩阵(向量乘矩阵时,m=1),最后会得到m*k阶矩阵,我们肯定希望点坐标经过矩阵变换后能够保持原来的维度,也就是用(x,y,z,w)的齐次坐标形式表示的,那么k应该为4,倒推回去,那么变换矩阵应该和齐次坐标向量有相同的列数。因此我们的变换矩阵是4*4的,而不是4*3的。
因此,我们就确定下来坐标空间变换的形式,在行主序的情况下,向量乘变换矩阵,二者前后顺序不可颠倒,即可得到变换后点的坐标。标准齐次坐标w=1。
当多个变换应用于同一点时,考虑到运算效率,我们通常会把多个变换矩阵相乘得到的最终结果去和点坐标做运算。比如先旋转,后平移。此处需特别注意,变换顺序不可更改,比如我想着是不是也可以先平移,后旋转?不行。为什么?看下面这幅图就知道了。
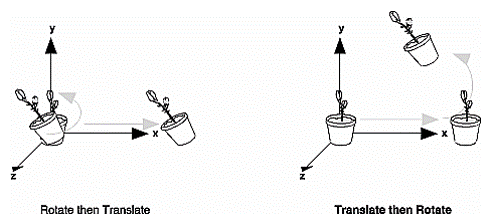
我们渲染管线中涉及的空间变换有如下几种
模型变换model transformation
视图变换view transformation
投影变换projection transformation
它们依次把顶点坐标从局部空间转换到世界空间,从世界空间转换到观察空间,从观察空间转换到投影空间。第一节我们已经讲了模型变换,不再赘述。
投影有平行投影和透视投影之分。正交投影就是无论离观察点是远是近,相同大小的东西看起来看起来仍然是相同大小。透视投影就是近大远小,和我们的生活常识相符。要投影就要有投影面,正交投影和透视投影的投影面分别如下:
正交投影
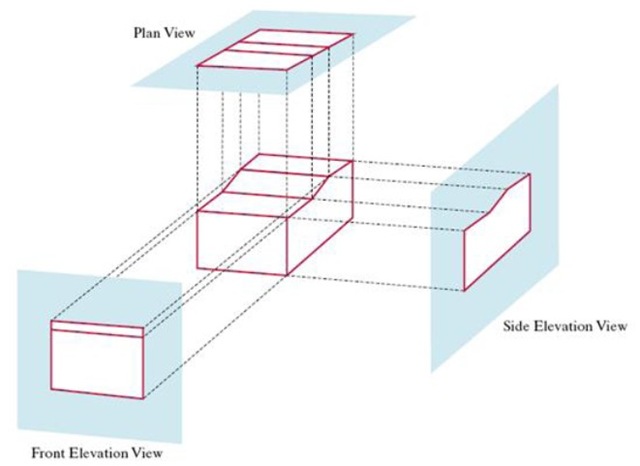
透视投影
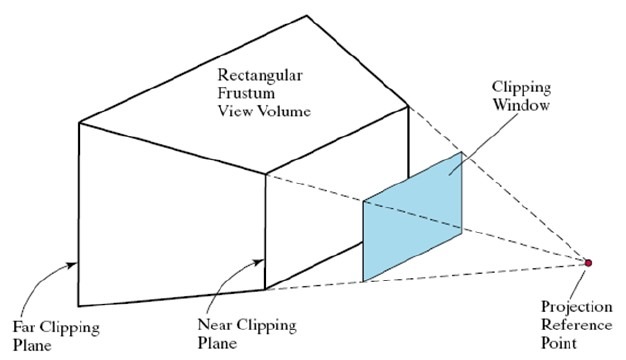
可以看到正交投影和透视投影都是用由六个投影面组成的“盒子”把视图变换的结果包围了起来。不同的是正交投影的盒子四四方方的;而透视投影的盒子是个放倒的四棱台,但我们在图形学里通常叫这个几何体为视平截体(view frustum)。
正交投影很简单,设一点(x,y,z),计算它在与zy轴组成的平面平行的投影面x=X0上的投影坐标时,过该点做射线与该投影面垂直,垂心即为投影点,其坐标便是(X0,y,z)。

透视投影就相对复杂一点。同样是投影,不是做点到投影面的垂线找垂心就行了,而是从视点(即四棱锥的顶点)出发,做经过该点的射线,该射线与投影面的交点即为该点在投影面上的投影点。听起来似乎有点儿复杂?看图:

其实就是个相似三角形的问题嘛。此外,这张图还向我们暗示了一个重要信息:在红线上的任意一点,无论d是多少,最后都会投影在(x1,y1,z1)这点。这意味着,大的物体在距视点较远时,会恰好被距视点较近的小物体遮住(其实是投影点重合了),这正符合透视投影的特点。
dx和opengl都为我们提供了简单的api可以直接建立起这样一个投影盒子。
正交投影所需参数就是六个面距观察坐标系Z轴的距离;
当ViewLeft=-ViewRight,ViewBottom=-ViewTop时,观察坐标系的Z轴穿过盒子中心,这意味着照相机观察到的视野在左右和上下方向延伸的同样远。
DX为这种通常做法提供了参数更为简化的api,只要提供盒子的宽和高以及前后面的Z值即可:
透视投影所需参数则是fov角度,投影面的宽高比w/h,近处投影面和远处投影面距视点的距离Znear和Zfar,好像很复杂?同样看图:

fov(field of view),其实就是视野所能及的最大角度,DX中我们用y方向上的视野角。通过fovy和aspect我们就可以求出fovx。
需要注意的是,归一化由图形设备自动完成,我们通过api得到的投影矩阵是经过归一化的最终结果。

Reference下就是全部api。
2、此外MS的网站上也可以查到相同的内容
https://msdn.microsoft.com/en-us/library/windows/desktop/ee663274(v=vs.85).aspx
资料参考:
1、原文: http://www.codeguru.com/cpp/misc/misc/math/article.php/c10123__1/Deriving-Projection-Matrices.htm译文:http://blog.csdn.net/zhanghua1816/article/details/23121735
2、http://dev.gameres.com/Program/Visual/3D/shenruTS.htm
3、http://blog.csdn.net/code_xbug/article/details/46299603
4、MS官方document-Tutorial04:3D Spaces
坐标空间概述
坐标空间,就是用不同的坐标系所度量的空间。不同的坐标系是什么意思呢?原点位置、坐标轴方向、坐标轴单位值,这三者决定了一个坐标系,任一不同,则坐标系不同。(这里决定坐标系的要素是我自己总结的,如有疏漏敬请指出)为什么图形学里要用到坐标空间变换呢?因为我们输入的模型顶点,通常都是定义在一个local space里的,也就是“局部坐标系”。这个坐标空间的特点就是,以模型上或者模型外一点为原点(通常在模型底心或中心),以正交的XYZ作为坐标轴(轴的方向定义通常与输入模型的面部朝向相关)。每一个输入的模型都有各自的Local space,当我们想把它在我们定义的世界空间里移动旋转缩放时,就面临着问题,因为我们执行的操作需要在一个统一的世界坐标系下执行。这时就需要用到坐标空间变换了——将一个局部坐标系下定义的顶点坐标,转换为世界坐标系下的顶点坐标。
图形学中共涉及以下几种坐标空间:
local space局部空间
world space世界空间
view space观察空间
projection space投影空间
screen space屏幕空间
将输入的模型最终显示到屏幕上,经过的空间变换也基本如上顺序所示。
那么,如何进行变换呢?
变换原理
对顶点进行空间变换,其实就是用不同坐标空间下的坐标值表示同一个点。一个点在三维空间下由三维向量xyz表示,运用变换矩阵,可以将其坐标进行空间变换。那么变换矩阵又是什么呢?变换矩阵既然能联系两种坐标空间,那么其组成元素必定和坐标轴相关。事实上,从坐标空间A变换到空间B,需要知道A的三个坐标轴向量及原点坐标在B下的表示。而这四个信息(XYZ轴方向向量,原点坐标在新坐标系下的表示)就构成了变换矩阵。
DX中采用行主序,这和OPENGL的列主序相反。这意味着在DX和OPENGL中,向量与矩阵相乘的顺序恰好相反。此处既然是学DX,那就按照DX的规矩来。
我画了一张示意图如下:

这是两个坐标空间,红色是空间A,黑色是空间B,二者Y轴方向相反。假设空间A的原点Oa在空间B下的坐标表示为(1,1,1)。那么从A变换到B,矩阵应该这么表示:

第一行是Xa,第二行是Ya,第三行是Za,第四行是Oa。这就是变换矩阵的基本形式。
注意到我们把每一行最后一个数都补齐了,凑出了第四列。其实,三维坐标空间内任一点,我们也都会表示为(x,y,z,w)。这就是“齐次坐标”。
为什么要引入齐次坐标?
在谈这个问题之前,我们先来看看如何矩阵和向量相乘是如何与三维变换关联起来的。我们最常用的三维变换有平移、旋转、缩放。
先不考虑和矩阵相乘,单看点的坐标如何变换。
设有一点(x0,y0,z0)
平移平移向量为(dx,dy,dz),那么平移结果就是(x0+dz,y0+dy,z0+dz);
旋转由于三维空间的旋转需要分绕x轴、绕y轴、绕z轴的情况分别来看,为了方便讲解,所以我们这里不妨从二维空间的旋转入手。旋转需要用到极坐标的知识(需要满足:1、直角坐标系原点与极坐标极点重合;2、直角坐标系x轴正向轴与极坐标极轴重合。具体请查阅极坐标与直角坐标的转换)。设旋转角度为θ,那么旋转结果就是(x0*cosθ+y0*(-sinθ),x0*sinθ+y0*cosθ);
缩放这就简单多了,设缩放因子为(sx,sy,sz),那么缩放结果就是(x0*sx,y0*sy,z0*sz)。
可以看出,平移是与原坐标做加法,旋转缩放是与原坐标做乘法。那么如果把这两类运算都用矩阵和向量做乘法来表示,那么我们会发现,乘法还好说,而加法就有问题了。因为我们是用(x,y,z)来表示坐标的,根据向量和矩阵相乘的运算法则,我们最终只可能得到各向量分量点乘的结果,无法凭空得到一个常量加法因子。这时我们就不得不引入一个额外的常量w来执行加法,这就是齐次坐标(x,y,z,w)的作用。(当然运用齐次坐标不止这一个好处)
现在点的坐标已经用齐次坐标表示了,那矩阵(注意是行主序)用四行三列来表示,也没什么问题吧?为什么我们要用四行四列的矩阵来表示变换矩阵?其实很简单,行主序的矩阵运算中,m*n矩阵乘n*k矩阵(向量乘矩阵时,m=1),最后会得到m*k阶矩阵,我们肯定希望点坐标经过矩阵变换后能够保持原来的维度,也就是用(x,y,z,w)的齐次坐标形式表示的,那么k应该为4,倒推回去,那么变换矩阵应该和齐次坐标向量有相同的列数。因此我们的变换矩阵是4*4的,而不是4*3的。
因此,我们就确定下来坐标空间变换的形式,在行主序的情况下,向量乘变换矩阵,二者前后顺序不可颠倒,即可得到变换后点的坐标。标准齐次坐标w=1。
当多个变换应用于同一点时,考虑到运算效率,我们通常会把多个变换矩阵相乘得到的最终结果去和点坐标做运算。比如先旋转,后平移。此处需特别注意,变换顺序不可更改,比如我想着是不是也可以先平移,后旋转?不行。为什么?看下面这幅图就知道了。

空间变换矩阵
上面讲到的变换其实是两种,一种是把点坐标从一个坐标空间转换到另一个坐标空间,另一种是把点坐标进行三维变换(平移、旋转、缩放)。这一节我们来看看第一类变换,用于坐标空间变换的矩阵。我们渲染管线中涉及的空间变换有如下几种
模型变换model transformation
视图变换view transformation
投影变换projection transformation
它们依次把顶点坐标从局部空间转换到世界空间,从世界空间转换到观察空间,从观察空间转换到投影空间。第一节我们已经讲了模型变换,不再赘述。
视图变换
观察空间,其实是我们从“照相机”看出去的空间。所观察到的世界空间,可以理解为从照相机的取景器中看到的。视图变换就是把世界空间中的物体转换到我们的取景器中来。按照之前我们对模型变换的解释,要执行视图变换,那么需要知道世界坐标系在观察坐标系中的表示。但是,照相机也可以看做世界空间下的一个物体,我们不妨反过来,求观察坐标系在世界坐标系下的表示,这就容易多了,因为世界坐标系定义在比观察坐标系大的多的空间中,求观察坐标系的位置和求一个普通物体在世界中的位置并没什么不同。只需要注意一点,求出的矩阵是视图变换矩阵的逆矩阵,与点坐标运算时需要取逆后再相乘。投影变换
顶点经过视图变换后,仍然是三维的,而我们的显示屏是一个二维的面,我们最终看到的是一个三维拍扁而成的投影面。所以投影变换讨论的就是如何处理三维坐标,让它们能够在二维平面上正常显示。但有必要说明的是,投影变换的结果——各个顶点——并不是直接分布在我们最后看到的二维平面,它们仍然分布在一个三维的“盒子”空间里,并且这个盒子的空间范围被限定在(-1~1,-1~1,0~1),这是图形设备执行归一化的结果。投影有平行投影和透视投影之分。正交投影就是无论离观察点是远是近,相同大小的东西看起来看起来仍然是相同大小。透视投影就是近大远小,和我们的生活常识相符。要投影就要有投影面,正交投影和透视投影的投影面分别如下:
正交投影

透视投影

可以看到正交投影和透视投影都是用由六个投影面组成的“盒子”把视图变换的结果包围了起来。不同的是正交投影的盒子四四方方的;而透视投影的盒子是个放倒的四棱台,但我们在图形学里通常叫这个几何体为视平截体(view frustum)。
正交投影很简单,设一点(x,y,z),计算它在与zy轴组成的平面平行的投影面x=X0上的投影坐标时,过该点做射线与该投影面垂直,垂心即为投影点,其坐标便是(X0,y,z)。

透视投影就相对复杂一点。同样是投影,不是做点到投影面的垂线找垂心就行了,而是从视点(即四棱锥的顶点)出发,做经过该点的射线,该射线与投影面的交点即为该点在投影面上的投影点。听起来似乎有点儿复杂?看图:

其实就是个相似三角形的问题嘛。此外,这张图还向我们暗示了一个重要信息:在红线上的任意一点,无论d是多少,最后都会投影在(x1,y1,z1)这点。这意味着,大的物体在距视点较远时,会恰好被距视点较近的小物体遮住(其实是投影点重合了),这正符合透视投影的特点。
归一化
无论哪种投影,投影坐标系的建立都是基于观察坐标系的,而不是世界坐标系。在投影变换之后,投影盒子都会被图形设备执行归一化——听起来玄乎,但其实就是把盒子内各点投射到一个(-1~1,-1~1,0~1)的“标准盒子”里。对于正交投影来说,由于归一化前后都是四四方方的盒子,所以运用平移-缩放就可以转化为标准盒子(先将投影盒子平移到中心与观察坐标系原点重合,然后在各个维度上执行缩放)。对于透视投影来说,归一化经过的数学步骤就更多一些,因为归一化前我们的盒子长得像个棱台。关于如何对透视投影进行归一化,具体的数学推导可见资料参考的第一个链接。dx和opengl都为我们提供了简单的api可以直接建立起这样一个投影盒子。
正交投影所需参数就是六个面距观察坐标系Z轴的距离;
XMMATRIX XMMatrixOrthographicOffCenterLH ( FLOAT ViewLeft, FLOAT ViewRight, FLOAT ViewBottom, FLOAT ViewTop, FLOAT NearZ, FLOAT FarZ )
当ViewLeft=-ViewRight,ViewBottom=-ViewTop时,观察坐标系的Z轴穿过盒子中心,这意味着照相机观察到的视野在左右和上下方向延伸的同样远。
DX为这种通常做法提供了参数更为简化的api,只要提供盒子的宽和高以及前后面的Z值即可:
XMMATRIX XMMatrixOrthographicLH( [in] float ViewWidth, [in] float ViewHeight, [in] float NearZ, [in] float FarZ );
透视投影所需参数则是fov角度,投影面的宽高比w/h,近处投影面和远处投影面距视点的距离Znear和Zfar,好像很复杂?同样看图:

fov(field of view),其实就是视野所能及的最大角度,DX中我们用y方向上的视野角。通过fovy和aspect我们就可以求出fovx。
XMMATRIX XMMatrixPerspectiveFovLH ( FLOAT FovAngleY, FLOAT AspectRatio, FLOAT NearZ, FLOAT FarZ )
需要注意的是,归一化由图形设备自动完成,我们通过api得到的投影矩阵是经过归一化的最终结果。
查询DX的api
1、官方的sdk下载下来,在Documentation\DirectX9下有directx_sdk.chm
Reference下就是全部api。
2、此外MS的网站上也可以查到相同的内容
https://msdn.microsoft.com/en-us/library/windows/desktop/ee663274(v=vs.85).aspx
相关文章推荐
- C#实现图形位置组合转换的方法
- C#实现判断图形文件格式的方法
- C#实现图形路径变换的方法
- php生成图形验证码几种方法小结
- CentOS的图形安装及初始环境设置教程
- C#实现图形区域组合操作的方法
- php实现图形显示Ip地址的代码及注释
- Java Web开发之图形验证码的生成与使用方法
- android中图形图像处理之drawable用法分析
- Android编程开发之在Canvas中利用Path绘制基本图形(圆形,矩形,椭圆,三角形等)
- Android开发之图形图像与动画(五)LayoutAnimationController详解
- C++实现图形界面时钟表盘代码
- C++实现二维图形的傅里叶变换
- Java在Linux下 不能处理图形的解决办法 分享
- python开发之tkinter实现图形随鼠标移动的方法
- 北京图王软件开发有限公司产品介绍
- PB做的史上最强的矢量画图软件(VISIO也要低头)
- 一次接线图的图符设计
- 一次接线图的图形概要设计
- 电力行业的图形应用概谈
