Codeforce 题目621C Wet Shark and Flowers(期望)
2016-02-01 02:43
483 查看
C. Wet Shark and Flowers
time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output
There are n sharks who grow flowers for Wet Shark. They are all sitting around the table, such that sharks i and i + 1 are
neighbours for all i from 1 to n - 1.
Sharks n and 1 are
neighbours too.
Each shark will grow some number of flowers si.
For i-th shark value si is
random integer equiprobably chosen in range from li to ri.
Wet Shark has it's favourite prime number p, and he really likes it! If for any pair of neighbouring sharks i and j the
product si·sj is
divisible by p, then Wet Shark becomes happy and gives 1000 dollars
to each of these sharks.
At the end of the day sharks sum all the money Wet Shark granted to them. Find the expectation of this value.
Input
The first line of the input contains two space-separated integers n and p (3 ≤ n ≤ 100 000, 2 ≤ p ≤ 109) —
the number of sharks and Wet Shark's favourite prime number. It is guaranteed that p is prime.
The i-th of the following n lines
contains information about i-th shark — two space-separated integers li and ri (1 ≤ li ≤ ri ≤ 109),
the range of flowers shark i can produce. Remember that si is
chosen equiprobably among all integers from li to ri,
inclusive.
Output
Print a single real number — the expected number of dollars that the sharks receive in total. You answer will be considered correct if its absolute or relative error does not exceed 10 - 6.
Namely: let's assume that your answer is a, and the answer of the jury is b.
The checker program will consider your answer correct, if

.
Sample test(s)
input
output
input
output
Note
A prime number is a positive integer number that is divisible only by 1 and itself. 1 is
not considered to be prime.
Consider the first sample. First shark grows some number of flowers from 1 to 2,
second sharks grows from 420 to 421 flowers
and third from 420420 to 420421.
There are eight cases for the quantities of flowers (s0, s1, s2) each
shark grows:
(1, 420, 420420): note that s0·s1 = 420, s1·s2 = 176576400,
and s2·s0 = 420420.
For each pair, 1000 dollars will be awarded to each shark. Therefore, each shark will be awarded 2000 dollars,
for a total of 6000 dollars.
(1, 420, 420421): now, the product s2·s0 is
not divisible by 2. Therefore, sharks s0 and s2 will
receive 1000 dollars, while shark s1will
receive 2000. The total is 4000.
(1, 421, 420420): total is 4000
(1, 421, 420421): total is 0.
(2, 420, 420420): total is 6000.
(2, 420, 420421): total is 6000.
(2, 421, 420420): total is 6000.
(2, 421, 420421): total is 4000.
The expected value is
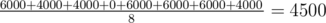
.
In the second sample, no combination of quantities will garner the sharks any money.
看样例还以为是保留1位小数的,提交一发不对,又读了一遍,发现没说保留几位,直接%lf输出,居然就过了。。
题目大意:输入个n和质数p,n个区间,每个区间可以等概率的任选一个数,如果选的这个区间和它下个区间选的数的积是p的倍数的话(n的下个是1),就挣2000,问挣的期望
思路:如果两个数的乘积是素数p的倍数的话,一定有一个是p的倍数。1减去两个都没取到p倍数的概率就好,然后for加一下
ac代码
time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output
There are n sharks who grow flowers for Wet Shark. They are all sitting around the table, such that sharks i and i + 1 are
neighbours for all i from 1 to n - 1.
Sharks n and 1 are
neighbours too.
Each shark will grow some number of flowers si.
For i-th shark value si is
random integer equiprobably chosen in range from li to ri.
Wet Shark has it's favourite prime number p, and he really likes it! If for any pair of neighbouring sharks i and j the
product si·sj is
divisible by p, then Wet Shark becomes happy and gives 1000 dollars
to each of these sharks.
At the end of the day sharks sum all the money Wet Shark granted to them. Find the expectation of this value.
Input
The first line of the input contains two space-separated integers n and p (3 ≤ n ≤ 100 000, 2 ≤ p ≤ 109) —
the number of sharks and Wet Shark's favourite prime number. It is guaranteed that p is prime.
The i-th of the following n lines
contains information about i-th shark — two space-separated integers li and ri (1 ≤ li ≤ ri ≤ 109),
the range of flowers shark i can produce. Remember that si is
chosen equiprobably among all integers from li to ri,
inclusive.
Output
Print a single real number — the expected number of dollars that the sharks receive in total. You answer will be considered correct if its absolute or relative error does not exceed 10 - 6.
Namely: let's assume that your answer is a, and the answer of the jury is b.
The checker program will consider your answer correct, if

.
Sample test(s)
input
3 2 1 2 420 421 420420 420421
output
4500.0
input
3 5 1 4 2 3 11 14
output
0.0
Note
A prime number is a positive integer number that is divisible only by 1 and itself. 1 is
not considered to be prime.
Consider the first sample. First shark grows some number of flowers from 1 to 2,
second sharks grows from 420 to 421 flowers
and third from 420420 to 420421.
There are eight cases for the quantities of flowers (s0, s1, s2) each
shark grows:
(1, 420, 420420): note that s0·s1 = 420, s1·s2 = 176576400,
and s2·s0 = 420420.
For each pair, 1000 dollars will be awarded to each shark. Therefore, each shark will be awarded 2000 dollars,
for a total of 6000 dollars.
(1, 420, 420421): now, the product s2·s0 is
not divisible by 2. Therefore, sharks s0 and s2 will
receive 1000 dollars, while shark s1will
receive 2000. The total is 4000.
(1, 421, 420420): total is 4000
(1, 421, 420421): total is 0.
(2, 420, 420420): total is 6000.
(2, 420, 420421): total is 6000.
(2, 421, 420420): total is 6000.
(2, 421, 420421): total is 4000.
The expected value is
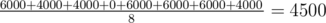
.
In the second sample, no combination of quantities will garner the sharks any money.
看样例还以为是保留1位小数的,提交一发不对,又读了一遍,发现没说保留几位,直接%lf输出,居然就过了。。
题目大意:输入个n和质数p,n个区间,每个区间可以等概率的任选一个数,如果选的这个区间和它下个区间选的数的积是p的倍数的话(n的下个是1),就挣2000,问挣的期望
思路:如果两个数的乘积是素数p的倍数的话,一定有一个是p的倍数。1减去两个都没取到p倍数的概率就好,然后for加一下
ac代码
#include<stdio.h>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
#include<string.h>
#define LL __int64
using namespace std;
double p[100100];
int main()
{
int n,m;
while(scanf("%d%d",&n,&m)!=EOF)
{
int i;
for(i=1;i<=n;i++)
{
int l,r;
scanf("%d%d",&l,&r);
int temp=(r/m-l/m);
if(l%m==0)
temp++;
p[i]=1.0-(double)temp/(r-l+1);
}
double ans=0;
for(i=1;i<n;i++)
{
ans+=(1-p[i]*p[i+1])*2000;
}
ans+=(1-p
*p[1])*2000;
printf("%lf\n",ans);
}
}
相关文章推荐
- 一个简单的DBHelper
- 视频课程计划
- java 将微信录音amr转换为mp3格式
- 在 Windows 平台上运行 FreeRTOS 示例程序
- deep learning framework(不同的深度学习框架)
- 第一篇博客
- weiphp 3.0创建插件提示错误解决办法 提示您没有创建目录写入权限,
- 编程模拟自然(六):如何画一颗动态树
- [傅里叶变换及其应用学习笔记] 二十九. 高维Ш函数修改版
- 密码学初级教程(四)单向散列函数-指纹-
- Codeforces 621B Wet Shark and Bishops(判定对角线点+组合数统计)
- 密码学初级教程(八)SSL/TLS-为了更安全的通信
- 一次郁闷的58同城经历
- 记录Android-Studio遇到的各种坑
- openCV学习记录:滤镜:霓虹&曝光
- 出现error: unable to create file tests/P_str_escape/str\\escape.rs的解决办法
- resultType跟resultMap不能同时存在
- Codeforces Round #341 (Div. 2) C. Wet Shark and Flowers
- Codeforces 621A Wet Shark and Odd and Even
- Divide and conquer:Sumsets(POJ 2549)
