Expectation maximization - EM算法学习总结
2015-12-17 17:25
253 查看
原创博客,转载请注明出处 Leavingseason /article/5230110.html
EM框架是一种求解最大似然概率估计的方法。往往用在存在隐藏变量的问题上。我这里特意用"框架"来称呼它,是因为EM算法不像一些常见的机器学习算法例如logistic regression, decision tree,只要把数据的输入输出格式固定了,直接调用工具包就可以使用。可以概括为一个两步骤的框架:
E-step:估计隐藏变量的概率分布期望函数(往往称之为Q函数

,它的定义在下面会详细给出);
M-step:求出使得Q函数最大的一组参数
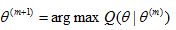
实际使用过程中,我们先要根据不同的问题先推导出Q函数,再套用E-M两步骤的框架。
下面来具体介绍为什么要引入EM算法?
不妨把问题的全部变量集(complete data)标记为X,可观测的变量集为Y,隐藏变量集为Z,其中X = (Y , Z) . 例如下图的HMM例子, S是隐变量,Y是观测值:

又例如,在GMM模型中(下文有实例) ,Y是所有观测到的点,z_i 表示 y_i 来自哪一个高斯分量,这是未知的。
问题要求解的是一组参数
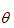
, 使得

最大。在求最大似然时,往往求的是对数最大:

(1)
对上式中的隐变量做积分(求和):
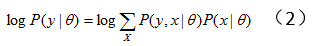
(2)式往往很难直接求解。于是产生了EM方法,此时我们想要最大化全变量(complete data)X的对数似然概率

:假设我们已经有了一个模型参数

的估计(第0时刻可以随机取一份初始值),基于这组模型参数我们可以求出一个此时刻X的概率分布函数。有了X的概率分布函数就可以写出

的期望函数,然后解出使得期望函数最大的

值,作为更新的

参数。基于这个更新的

再重复计算X的概率分布,以此迭代。流程如下:
Step 1: 随机选取初始值

Step 2:给定
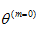
和观测变量Y, 计算条件概率分布

Step 3:在step4中我们想要最大化

,但是我们并不完全知道X(因为有一些隐变量),所以我们只好最大化

的期望值, 而X的概率分布也在step 2 中计算出来了。所以现在要做的就是求期望

,也称为Q函数:
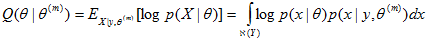
其中,
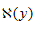
表示给定观测值y时所有可能的x取值范围,即
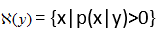
Step 4 求解
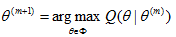
Step 5 回到step 2, 重复迭代下去。
为什么要通过引入Q函数来更新theta的值呢?因为它和我们的最大化终极目标(公式(1))有很微妙的关系:
定理1:

证明:在step4中,既然求解的是arg max, 那么必然有

。于是:

其中,(3)到(4)是因为X=(Y , Z), y=T(x), T是某种确定函数,所以当x确定了,y也就确定了(但反之不成立);即:

而(4)中的log里面项因为不包含被积分变量x,所以可以直接提到积分外面。
所以E-M算法的每一次迭代,都不会使目标值变得更差。但是EM的结果并不能保证是全局最优的,有可能收敛到局部最优解。所以实际使用中还需要多取几种初始值试验。
实例:高斯混合模型GMM
假设从一个包含k个分量的高斯混合模型中随机独立采样了n个点
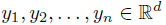
, 现在要估计所有高斯分量的参数

。 例如图(a)就是一个k=3的一维GMM。

高斯分布函数为:

令

为第m次迭代时,第i个点来自第j个高斯分量的概率,那么:
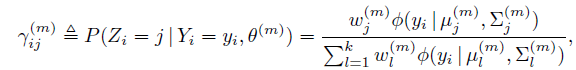
并且

因为每个点是独立的,不难证明有:

于是首先写出每个

:

忽略常数项,求和,完成E-step:

为简化表达,再令

,
Q函数变为:
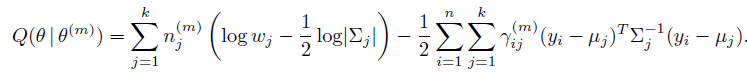
现在到了M-step了,我们要解出使得Q函数最大化的参数。最简单地做法是求导数为0的值。
首先求w。 因为w有一个约束:

可以使用拉格朗日乘子方法。 除去和w无关的项,写出新的目标函数:
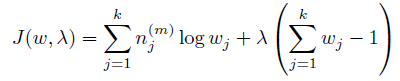
求导:
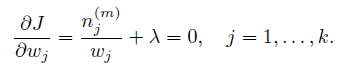
很容易解出w:

同理解出其他参数:



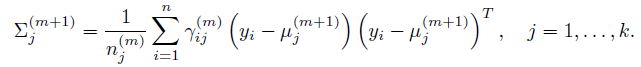
总结:个人觉得,EM算法里面最难懂的是Q函数。初次看教程的时候,

很能迷惑人,要弄清楚

是变量,是需要求解的;

是已知量,是从上一轮迭代推导出的值。
EM框架是一种求解最大似然概率估计的方法。往往用在存在隐藏变量的问题上。我这里特意用"框架"来称呼它,是因为EM算法不像一些常见的机器学习算法例如logistic regression, decision tree,只要把数据的输入输出格式固定了,直接调用工具包就可以使用。可以概括为一个两步骤的框架:
E-step:估计隐藏变量的概率分布期望函数(往往称之为Q函数

,它的定义在下面会详细给出);
M-step:求出使得Q函数最大的一组参数
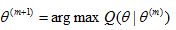
实际使用过程中,我们先要根据不同的问题先推导出Q函数,再套用E-M两步骤的框架。
下面来具体介绍为什么要引入EM算法?
不妨把问题的全部变量集(complete data)标记为X,可观测的变量集为Y,隐藏变量集为Z,其中X = (Y , Z) . 例如下图的HMM例子, S是隐变量,Y是观测值:

又例如,在GMM模型中(下文有实例) ,Y是所有观测到的点,z_i 表示 y_i 来自哪一个高斯分量,这是未知的。
问题要求解的是一组参数
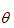
, 使得

最大。在求最大似然时,往往求的是对数最大:

(1)
对上式中的隐变量做积分(求和):
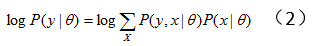
(2)式往往很难直接求解。于是产生了EM方法,此时我们想要最大化全变量(complete data)X的对数似然概率

:假设我们已经有了一个模型参数

的估计(第0时刻可以随机取一份初始值),基于这组模型参数我们可以求出一个此时刻X的概率分布函数。有了X的概率分布函数就可以写出

的期望函数,然后解出使得期望函数最大的

值,作为更新的

参数。基于这个更新的

再重复计算X的概率分布,以此迭代。流程如下:
Step 1: 随机选取初始值

Step 2:给定
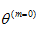
和观测变量Y, 计算条件概率分布

Step 3:在step4中我们想要最大化

,但是我们并不完全知道X(因为有一些隐变量),所以我们只好最大化

的期望值, 而X的概率分布也在step 2 中计算出来了。所以现在要做的就是求期望

,也称为Q函数:
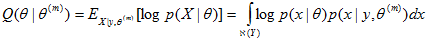
其中,
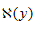
表示给定观测值y时所有可能的x取值范围,即
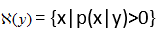
Step 4 求解
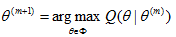
Step 5 回到step 2, 重复迭代下去。
为什么要通过引入Q函数来更新theta的值呢?因为它和我们的最大化终极目标(公式(1))有很微妙的关系:
定理1:

证明:在step4中,既然求解的是arg max, 那么必然有

。于是:

其中,(3)到(4)是因为X=(Y , Z), y=T(x), T是某种确定函数,所以当x确定了,y也就确定了(但反之不成立);即:

而(4)中的log里面项因为不包含被积分变量x,所以可以直接提到积分外面。
所以E-M算法的每一次迭代,都不会使目标值变得更差。但是EM的结果并不能保证是全局最优的,有可能收敛到局部最优解。所以实际使用中还需要多取几种初始值试验。
实例:高斯混合模型GMM
假设从一个包含k个分量的高斯混合模型中随机独立采样了n个点
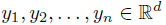
, 现在要估计所有高斯分量的参数

。 例如图(a)就是一个k=3的一维GMM。

高斯分布函数为:

令

为第m次迭代时,第i个点来自第j个高斯分量的概率,那么:
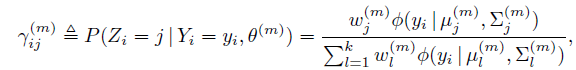
并且

因为每个点是独立的,不难证明有:

于是首先写出每个

:

忽略常数项,求和,完成E-step:

为简化表达,再令

,
Q函数变为:
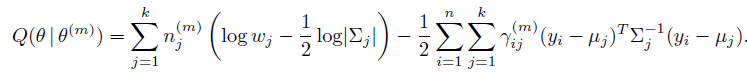
现在到了M-step了,我们要解出使得Q函数最大化的参数。最简单地做法是求导数为0的值。
首先求w。 因为w有一个约束:

可以使用拉格朗日乘子方法。 除去和w无关的项,写出新的目标函数:
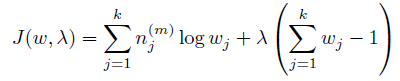
求导:
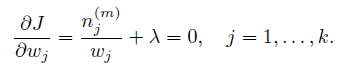
很容易解出w:

同理解出其他参数:



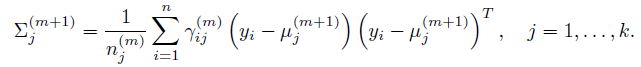
总结:个人觉得,EM算法里面最难懂的是Q函数。初次看教程的时候,

很能迷惑人,要弄清楚

是变量,是需要求解的;

是已知量,是从上一轮迭代推导出的值。
相关文章推荐
- 网页上传文件,到服务器,再讲数据导入数据库
- easyui combobox 省市区三级联动
- AdaBoost装袋提升算法
- unity 发布web player版,网页打开报Failed to initialize player's 3D settings
- OpenGL(1)——环境搭建
- Android 6.0 动态申请权限
- 并发编程 Promise, Future 和 Callback
- CBA算法---基于关联规则进行分类的算法
- gSpan频繁子图挖掘算法
- 解决Xcode7.1上传成功但iTunesconnect一直不能构建版本的问题
- 学习问题笔记
- 如何成就自己的IT梦成为野生电脑维修高工
- react-native执行 npm install cl.exe找不到 的问题
- 删除sqlserver管理器登录信息缓存
- redis 学习手册之键key操作
- 1^3 +2^3+3^3+...+n^3
- spring浅谈
- WebView改变网页文字大小、颜色,背景颜色
- 密码输入框显示明文密码
- xcode中删除xcdatamodel中的Entity
