前向-后向算法(Forward-backward algorithm)
2015-11-30 11:31
281 查看
根据观察序列生成隐马尔科夫模型(Generating a HMM from a sequence of obersvations)
与HMM模型相关的“有用”的问题是评估(前向算法)和解码(维特比算法)——它们一个被用来测量一个模型的相对适用性,另一个被用来推测模型隐藏的部分在做什么(“到底发生了”什么)。可以看出它们都依赖于隐马尔科夫模型(HMM)参数这一先验知识——状态转移矩阵,混淆(观察)矩阵,以及

向量(初始化概率向量)。
然而,在许多实际问题的情况下这些参数都不能直接计算的,而要需要进行估计——这就是隐马尔科夫模型中的学习问题。前向-后向算法就可以以一个观察序列为基础来进行这样的估计,而这个观察序列来自于一个给定的集合,它所代表的是一个隐马尔科夫模型中的一个已知的隐藏集合。
一个例子可能是一个庞大的语音处理数据库,其底层的语音可能由一个马尔可夫过程基于已知的音素建模的,而其可以观察的部分可能由可识别的状态(可能通过一些矢量数据表示)建模的,但是没有(直接)的方式来获取隐马尔科夫模型(HMM)参数。
前向-后向算法并非特别难以理解,但自然地比前向算法和维特比算法更复杂。由于这个原因,这里就不详细讲解前向-后向算法了(任何有关HMM模型的参考文献都会提供这方面的资料的)。
总之,前向-后向算法首先对于隐马尔科夫模型的参数进行一个初始的估计(这很可能是完全错误的),然后通过对于给定的数据评估这些参数的的价值并减少它们所引起的错误来重新修订这些HMM参数。从这个意义上讲,它是以一种梯度下降的形式寻找一种错误测度的最小值。
之所以称其为前向-后向算法,主要是因为对于网格中的每一个状态,它既计算到达此状态的“前向”概率(给定当前模型的近似估计),又计算生成此模型最终状态的“后向”概率(给定当前模型的近似估计)。 这些都可以通过利用递归进行有利地计算,就像我们已经看到的。可以通过利用近似的HMM模型参数来提高这些中间概率进行调整,而这些调整又形成了前向-后向算法迭代的基础。
要理解前向-后向算法,首先需要了解两个算法:后向算法和EM算法。后向算法是必须的,因为前向-后向算法就是利用了前向算法与后向算法中的变量因子,其得名也因于此;而EM算法不是必须的,不过由于前向-后向算法是EM算法的一个特例,因此了解一下EM算法也是有好处的,说实话,对于EM算法,我也是云里雾里的。好了,废话少说,我们先谈谈后向算法。
1、后向算法(Backward algorithm)
其实如果理解了前向算法,后向算法也是比较好理解的,这里首先重新定义一下前向算法中的局部概率at(i),称其为前向变量,这也是为前向-后向算法做点准备:

相似地,我们也可以定义一个后向变量Bt(i)(同样可以理解为一个局部概率):
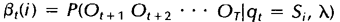
后向变量(局部概率)表示的是已知隐马尔科夫模型
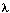
及t时刻位于隐藏状态Si这一事实,从t+1时刻到终止时刻的局部观察序列的概率。同样与前向算法相似,我们可以从后向前(故称之为后向算法)递归地计算后向变量:
1)初始化,令t=T时刻所有状态的后向变量为1:

2)归纳,递归计算每个时间点,t=T-1,T-2,…,1时的后向变量:
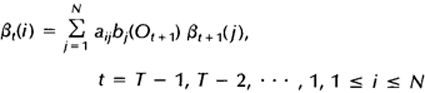
这样就可以计算每个时间点上所有的隐藏状态所对应的后向变量,如果需要利用后向算法计算观察序列的概率,只需将t=1时刻的后向变量(局部概率)相加即可。下图显示的是t+1时刻与t时刻的后向变量之间的关系:
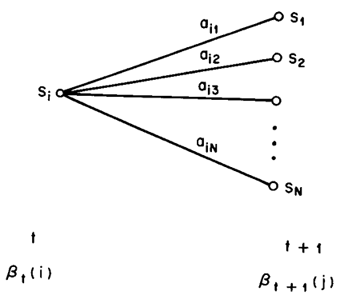
上述主要参考自HMM经典论文《A tutorial on Hidden Markov Models and selected applications in speech recognition》。下面我们给出利用后向算法计算观察序列概率的程序示例,这个程序仍然来自于UMDHMM。
后向算法程序示例如下(在backward.c中):
for (i = 1; i <= phmm->N; i++)
beta[T][i] = 1.0;
for (t = T - 1; t >= 1; t--)
{
for (i = 1; i <= phmm->N; i++)
{
sum = 0.0;
for (j = 1; j <= phmm->N; j++)
sum += phmm->A[i][j] *
(phmm->B[j][O[t+1]])*beta[t+1][j];
beta[t][i] = sum;
}
}
*pprob = 0.0;
for (i = 1; i <= phmm->N; i++)
*pprob += beta[1][i];
}
隐马尔科夫模型(HMM)的三个基本问题中,第三个HMM参数学习的问题是最难的,因为对于给定的观察序列O,没有任何一种方法可以精确地找到一组最优的隐马尔科夫模型参数(A、B、

)使P(O|
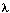
)最大。因而,学者们退而求其次,不能使P(O|
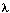
)全局最优,就寻求使其局部最优(最大化)的解决方法,而前向-后向算法(又称之为Baum-Welch算法)就成了隐马尔科夫模型学习问题的一种替代(近似)解决方法。
我们首先定义两个变量。给定观察序列O及隐马尔科夫模型
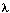
,定义t时刻位于隐藏状态Si的概率变量为:
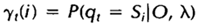
回顾一下第二节中关于前向变量at(i)及后向变量Bt(i)的定义,我们可以很容易地将上式用前向、后向变量表示为:
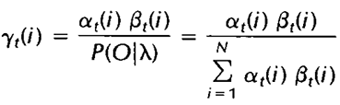
其中分母的作用是确保:
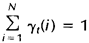
给定观察序列O及隐马尔科夫模型
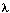
,定义t时刻位于隐藏状态Si及t+1时刻位于隐藏状态Sj的概率变量为:
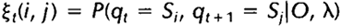
该变量在网格中所代表的关系如下图所示:
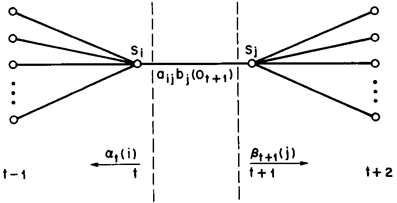
同样,该变量也可以由前向、后向变量表示:
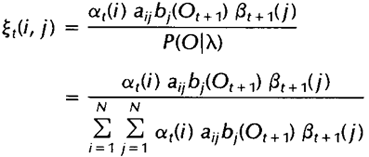
而上述定义的两个变量间也存在着如下关系:
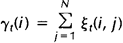
如果对于时间轴t上的所有
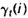
相加,我们可以得到一个总和,它可以被解释为从其他隐藏状态访问Si的期望值(网格中的所有时间的期望),或者,如果我们求和时不包括时间轴上的t=T时刻,那么它可以被解释为从隐藏状态Si出发的状态转移期望值。相似地,如果对
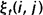
在时间轴t上求和(从t=1到t=T-1),那么该和可以被解释为从状态Si到状态Sj的状态转移期望值。即:

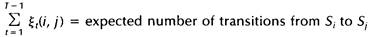
上一节我们定义了两个变量及相应的期望值,本节我们利用这两个变量及其期望值来重新估计隐马尔科夫模型(HMM)的参数

,A及B:

如果我们定义当前的HMM模型为
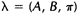
,那么可以利用该模型计算上面三个式子的右端;我们再定义重新估计的HMM模型为
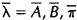
,那么上面三个式子的左端就是重估的HMM模型参数。Baum及他的同事在70年代证明了
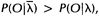
因此如果我们迭代地的计算上面三个式子,由此不断地重新估计HMM的参数,那么在多次迭代后可以得到的HMM模型的一个最大似然估计。不过需要注意的是,前向-后向算法所得的这个结果(最大似然估计)是一个局部最优解。
关于前向-后向算法和EM算法的具体关系的解释,大家可以参考HMM经典论文《A tutorial on Hidden Markov Models and selected applications in speech recognition》,这里就不详述了。下面我们给出UMDHMM中的前向-后向算法示例,这个算法比较复杂,这里只取主函数,其中所引用的函数大家如果感兴趣的话可以自行参考UMDHMM。
前向-后向算法程序示例如下(在baum.c中):
前向-后向算法就到此为止了。
double logprobf, logprobb, threshold;
double numeratorA, denominatorA;
double numeratorB, denominatorB;
double ***xi, *scale;
double delta, deltaprev, logprobprev;
deltaprev = 10e-70;
xi = AllocXi(T, phmm->N);
scale = dvector(1, T);
ForwardWithScale(phmm, T, O, alpha, scale, &logprobf);
*plogprobinit = logprobf;
BackwardWithScale(phmm, T, O, beta, scale, &logprobb);
ComputeGamma(phmm, T, alpha, beta, gamma);
ComputeXi(phmm, T, O, alpha, beta, xi);
logprobprev = logprobf;
do
{
for (i = 1; i <= phmm->N; i++)
phmm->pi[i] = .001 + .999*gamma[1][i];
for (i = 1; i <= phmm->N; i++)
{
denominatorA = 0.0;
for (t = 1; t <= T - 1; t++)
denominatorA += gamma[t][i];
for (j = 1; j <= phmm->N; j++)
{
numeratorA = 0.0;
for (t = 1; t <= T - 1; t++)
numeratorA += xi[t][i][j];
phmm->A[i][j] = .001 +
.999*numeratorA/denominatorA;
}
denominatorB = denominatorA + gamma[T][i];
for (k = 1; k <= phmm->M; k++)
{
numeratorB = 0.0;
for (t = 1; t <= T; t++)
{
if (O[t] == k)
numeratorB += gamma[t][i];
}
phmm->B[i][k] = .001 +
.999*numeratorB/denominatorB;
}
}
ForwardWithScale(phmm, T, O, alpha, scale, &logprobf);
BackwardWithScale(phmm, T, O, beta, scale, &logprobb);
ComputeGamma(phmm, T, alpha, beta, gamma);
ComputeXi(phmm, T, O, alpha, beta, xi);
delta = logprobf - logprobprev;
logprobprev = logprobf;
l++;
}
while (delta > DELTA);
*pniter = l;
*plogprobfinal = logprobf;
FreeXi(xi, T, phmm->N);
free_dvector(scale, 1, T);
}
总结(Summary)
通常,模式并不是单独的出现,而是作为时间序列中的一个部分——这个过程有时候可以被辅助用来对它们进行识别。在基于时间的进程中,通常都会使用一些假设——一个最常用的假设是进程的状态只依赖于前面N个状态——这样我们就有了一个N阶马尔科夫模型。最简单的例子是N = 1。
存在很多例子,在这些例子中进程的状态(模式)是不能够被直接观察的,但是可以非直接地,或者概率地被观察为模式的另外一种集合——这样我们就可以定义一类隐马尔科夫模型——这些模型已被证明在当前许多研究领域,尤其是语音识别领域具有非常大的价值。
在实际的过程中这些模型提出了三个问题都可以得到立即有效的解决,分别是:
* 评估:对于一个给定的隐马尔科夫模型其生成一个给定的观察序列的概率是多少。前向算法可以有效的解决此问题。
* 解码:什么样的隐藏(底层)状态序列最有可能生成一个给定的观察序列。维特比算法可以有效的解决此问题。
* 学习:对于一个给定的观察序列样本,什么样的模型最可能生成该序列——也就是说,该模型的参数是什么。这个问题可以通过使用前向-后向算法解决。
隐马尔科夫模型(HMM)在分析实际系统中已被证明有很大的价值;它们通常的缺点是过于简化的假设,这与马尔可夫假设相关——即一个状态只依赖于前一个状态,并且这种依赖关系是独立于时间之外的(与时间无关)。
关于隐马尔科夫模型的完整论述,可参阅:
L R Rabiner and B H Juang, `An introduction to HMMs’, iEEE ASSP Magazine, 3, 4-16.
与HMM模型相关的“有用”的问题是评估(前向算法)和解码(维特比算法)——它们一个被用来测量一个模型的相对适用性,另一个被用来推测模型隐藏的部分在做什么(“到底发生了”什么)。可以看出它们都依赖于隐马尔科夫模型(HMM)参数这一先验知识——状态转移矩阵,混淆(观察)矩阵,以及

向量(初始化概率向量)。
然而,在许多实际问题的情况下这些参数都不能直接计算的,而要需要进行估计——这就是隐马尔科夫模型中的学习问题。前向-后向算法就可以以一个观察序列为基础来进行这样的估计,而这个观察序列来自于一个给定的集合,它所代表的是一个隐马尔科夫模型中的一个已知的隐藏集合。
一个例子可能是一个庞大的语音处理数据库,其底层的语音可能由一个马尔可夫过程基于已知的音素建模的,而其可以观察的部分可能由可识别的状态(可能通过一些矢量数据表示)建模的,但是没有(直接)的方式来获取隐马尔科夫模型(HMM)参数。
前向-后向算法并非特别难以理解,但自然地比前向算法和维特比算法更复杂。由于这个原因,这里就不详细讲解前向-后向算法了(任何有关HMM模型的参考文献都会提供这方面的资料的)。
总之,前向-后向算法首先对于隐马尔科夫模型的参数进行一个初始的估计(这很可能是完全错误的),然后通过对于给定的数据评估这些参数的的价值并减少它们所引起的错误来重新修订这些HMM参数。从这个意义上讲,它是以一种梯度下降的形式寻找一种错误测度的最小值。
之所以称其为前向-后向算法,主要是因为对于网格中的每一个状态,它既计算到达此状态的“前向”概率(给定当前模型的近似估计),又计算生成此模型最终状态的“后向”概率(给定当前模型的近似估计)。 这些都可以通过利用递归进行有利地计算,就像我们已经看到的。可以通过利用近似的HMM模型参数来提高这些中间概率进行调整,而这些调整又形成了前向-后向算法迭代的基础。
要理解前向-后向算法,首先需要了解两个算法:后向算法和EM算法。后向算法是必须的,因为前向-后向算法就是利用了前向算法与后向算法中的变量因子,其得名也因于此;而EM算法不是必须的,不过由于前向-后向算法是EM算法的一个特例,因此了解一下EM算法也是有好处的,说实话,对于EM算法,我也是云里雾里的。好了,废话少说,我们先谈谈后向算法。
1、后向算法(Backward algorithm)
其实如果理解了前向算法,后向算法也是比较好理解的,这里首先重新定义一下前向算法中的局部概率at(i),称其为前向变量,这也是为前向-后向算法做点准备:

相似地,我们也可以定义一个后向变量Bt(i)(同样可以理解为一个局部概率):
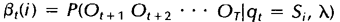
后向变量(局部概率)表示的是已知隐马尔科夫模型
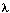
及t时刻位于隐藏状态Si这一事实,从t+1时刻到终止时刻的局部观察序列的概率。同样与前向算法相似,我们可以从后向前(故称之为后向算法)递归地计算后向变量:
1)初始化,令t=T时刻所有状态的后向变量为1:

2)归纳,递归计算每个时间点,t=T-1,T-2,…,1时的后向变量:
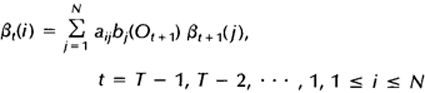
这样就可以计算每个时间点上所有的隐藏状态所对应的后向变量,如果需要利用后向算法计算观察序列的概率,只需将t=1时刻的后向变量(局部概率)相加即可。下图显示的是t+1时刻与t时刻的后向变量之间的关系:

上述主要参考自HMM经典论文《A tutorial on Hidden Markov Models and selected applications in speech recognition》。下面我们给出利用后向算法计算观察序列概率的程序示例,这个程序仍然来自于UMDHMM。
后向算法程序示例如下(在backward.c中):
void Backward(HMM *phmm, int T, int *O, double **beta, double *pprob)
{
int i, j;
int t;
double sum;for (i = 1; i <= phmm->N; i++)
beta[T][i] = 1.0;
for (t = T - 1; t >= 1; t--)
{
for (i = 1; i <= phmm->N; i++)
{
sum = 0.0;
for (j = 1; j <= phmm->N; j++)
sum += phmm->A[i][j] *
(phmm->B[j][O[t+1]])*beta[t+1][j];
beta[t][i] = sum;
}
}
*pprob = 0.0;
for (i = 1; i <= phmm->N; i++)
*pprob += beta[1][i];
}
隐马尔科夫模型(HMM)的三个基本问题中,第三个HMM参数学习的问题是最难的,因为对于给定的观察序列O,没有任何一种方法可以精确地找到一组最优的隐马尔科夫模型参数(A、B、

)使P(O|
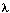
)最大。因而,学者们退而求其次,不能使P(O|
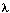
)全局最优,就寻求使其局部最优(最大化)的解决方法,而前向-后向算法(又称之为Baum-Welch算法)就成了隐马尔科夫模型学习问题的一种替代(近似)解决方法。
我们首先定义两个变量。给定观察序列O及隐马尔科夫模型
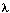
,定义t时刻位于隐藏状态Si的概率变量为:
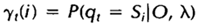
回顾一下第二节中关于前向变量at(i)及后向变量Bt(i)的定义,我们可以很容易地将上式用前向、后向变量表示为:
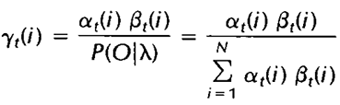
其中分母的作用是确保:
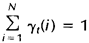
给定观察序列O及隐马尔科夫模型
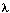
,定义t时刻位于隐藏状态Si及t+1时刻位于隐藏状态Sj的概率变量为:
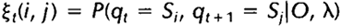
该变量在网格中所代表的关系如下图所示:

同样,该变量也可以由前向、后向变量表示:
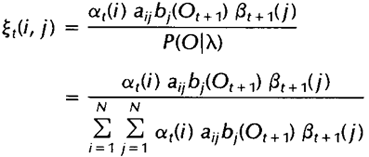
而上述定义的两个变量间也存在着如下关系:
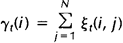
如果对于时间轴t上的所有
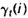
相加,我们可以得到一个总和,它可以被解释为从其他隐藏状态访问Si的期望值(网格中的所有时间的期望),或者,如果我们求和时不包括时间轴上的t=T时刻,那么它可以被解释为从隐藏状态Si出发的状态转移期望值。相似地,如果对
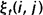
在时间轴t上求和(从t=1到t=T-1),那么该和可以被解释为从状态Si到状态Sj的状态转移期望值。即:

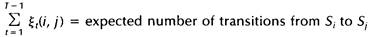
上一节我们定义了两个变量及相应的期望值,本节我们利用这两个变量及其期望值来重新估计隐马尔科夫模型(HMM)的参数

,A及B:

如果我们定义当前的HMM模型为
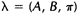
,那么可以利用该模型计算上面三个式子的右端;我们再定义重新估计的HMM模型为
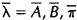
,那么上面三个式子的左端就是重估的HMM模型参数。Baum及他的同事在70年代证明了
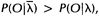
因此如果我们迭代地的计算上面三个式子,由此不断地重新估计HMM的参数,那么在多次迭代后可以得到的HMM模型的一个最大似然估计。不过需要注意的是,前向-后向算法所得的这个结果(最大似然估计)是一个局部最优解。
关于前向-后向算法和EM算法的具体关系的解释,大家可以参考HMM经典论文《A tutorial on Hidden Markov Models and selected applications in speech recognition》,这里就不详述了。下面我们给出UMDHMM中的前向-后向算法示例,这个算法比较复杂,这里只取主函数,其中所引用的函数大家如果感兴趣的话可以自行参考UMDHMM。
前向-后向算法程序示例如下(在baum.c中):
void BaumWelch(HMM *phmm, int T, int *O, double **alpha, double **beta, double **gamma, int *pniter, double *plogprobinit, double *plogprobfinal)
{
int i, j, k;
int t, l = 0;前向-后向算法就到此为止了。
double logprobf, logprobb, threshold;
double numeratorA, denominatorA;
double numeratorB, denominatorB;
double ***xi, *scale;
double delta, deltaprev, logprobprev;
deltaprev = 10e-70;
xi = AllocXi(T, phmm->N);
scale = dvector(1, T);
ForwardWithScale(phmm, T, O, alpha, scale, &logprobf);
*plogprobinit = logprobf;
BackwardWithScale(phmm, T, O, beta, scale, &logprobb);
ComputeGamma(phmm, T, alpha, beta, gamma);
ComputeXi(phmm, T, O, alpha, beta, xi);
logprobprev = logprobf;
do
{
for (i = 1; i <= phmm->N; i++)
phmm->pi[i] = .001 + .999*gamma[1][i];
for (i = 1; i <= phmm->N; i++)
{
denominatorA = 0.0;
for (t = 1; t <= T - 1; t++)
denominatorA += gamma[t][i];
for (j = 1; j <= phmm->N; j++)
{
numeratorA = 0.0;
for (t = 1; t <= T - 1; t++)
numeratorA += xi[t][i][j];
phmm->A[i][j] = .001 +
.999*numeratorA/denominatorA;
}
denominatorB = denominatorA + gamma[T][i];
for (k = 1; k <= phmm->M; k++)
{
numeratorB = 0.0;
for (t = 1; t <= T; t++)
{
if (O[t] == k)
numeratorB += gamma[t][i];
}
phmm->B[i][k] = .001 +
.999*numeratorB/denominatorB;
}
}
ForwardWithScale(phmm, T, O, alpha, scale, &logprobf);
BackwardWithScale(phmm, T, O, beta, scale, &logprobb);
ComputeGamma(phmm, T, alpha, beta, gamma);
ComputeXi(phmm, T, O, alpha, beta, xi);
delta = logprobf - logprobprev;
logprobprev = logprobf;
l++;
}
while (delta > DELTA);
*pniter = l;
*plogprobfinal = logprobf;
FreeXi(xi, T, phmm->N);
free_dvector(scale, 1, T);
}
总结(Summary)
通常,模式并不是单独的出现,而是作为时间序列中的一个部分——这个过程有时候可以被辅助用来对它们进行识别。在基于时间的进程中,通常都会使用一些假设——一个最常用的假设是进程的状态只依赖于前面N个状态——这样我们就有了一个N阶马尔科夫模型。最简单的例子是N = 1。
存在很多例子,在这些例子中进程的状态(模式)是不能够被直接观察的,但是可以非直接地,或者概率地被观察为模式的另外一种集合——这样我们就可以定义一类隐马尔科夫模型——这些模型已被证明在当前许多研究领域,尤其是语音识别领域具有非常大的价值。
在实际的过程中这些模型提出了三个问题都可以得到立即有效的解决,分别是:
* 评估:对于一个给定的隐马尔科夫模型其生成一个给定的观察序列的概率是多少。前向算法可以有效的解决此问题。
* 解码:什么样的隐藏(底层)状态序列最有可能生成一个给定的观察序列。维特比算法可以有效的解决此问题。
* 学习:对于一个给定的观察序列样本,什么样的模型最可能生成该序列——也就是说,该模型的参数是什么。这个问题可以通过使用前向-后向算法解决。
隐马尔科夫模型(HMM)在分析实际系统中已被证明有很大的价值;它们通常的缺点是过于简化的假设,这与马尔可夫假设相关——即一个状态只依赖于前一个状态,并且这种依赖关系是独立于时间之外的(与时间无关)。
关于隐马尔科夫模型的完整论述,可参阅:
L R Rabiner and B H Juang, `An introduction to HMMs’, iEEE ASSP Magazine, 3, 4-16.
相关文章推荐
- API To Import Negotiations(转)
- Django-数据模型
- GO比较容易混淆的地方
- 如何用好Google、百度等搜索引擎
- 【django】搭建博客教程(3)——markdown以及highlight
- history.back();history.go(-1);触发操作后无效解决方案
- tornado学习笔记:wtforms-tornado简单介绍
- gosn解析集合
- PS: Going Deeper With Convolutions___CVPR2015
- Go语言条件变量的两个例子
- 《Go语言入门》第一个Go语言程序——HelloWorld
- Go中的goroutine和channel使用
- 安装Django
- Go 语言Map(集合)
- Go 语言范围(Range)
- Go 语言切片(Slice)
- Go 语言结构体
- Go 语言指针
- 安装及配置GoClipse
- GO语言LiteIDE的安装使用
