克鲁斯卡尔算法
2015-11-29 19:27
369 查看
环境: Codeblocks 13.12 + GCC 4.7.1
参考资料:《大话数据结构》,《啊哈算法》,百度百科
基本思想:(1)构造一个只含n个顶点,边集为空的子图。若将图中各个顶点看成一棵树的根节点,则它是一个含有n棵树的森林。(2)从网的边集 E 中选取一条权值最小的边,若该条边的两个顶点分属不同的树,则将其加入子图。也就是说,将这两个顶点分别所在的两棵树合成一棵树;反之,若该条边的两个顶点已落在同一棵树上,则不可取,而应该取下一条权值最小的边再试之(3)依次类推,直至森林中只有一棵树,也即子图中含有 n-1条边为止。
大白话:(1)将图中的所有边都去掉。(2)将边按权值从小到大的顺序添加到图中,保证添加的过程中不会形成环(3)重复上一步直到连接所有顶点,此时就生成了最小生成树。这是一种贪心策略。
难点:判断某条边<u, v>的加入是否会在已经选定的边集集合中形成环。
解决办法:使用并查集,分别找出两个顶点u, v所在树的根节点。若根节点相同,说明u, v在同一棵树中,则u, v连接起来会形成环;若根节点不同,则u, v不在一棵树中,连接起来不会形成环,而是将两棵树合并。
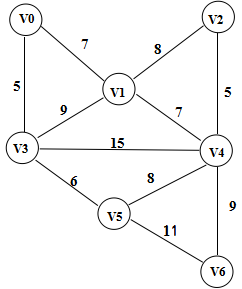
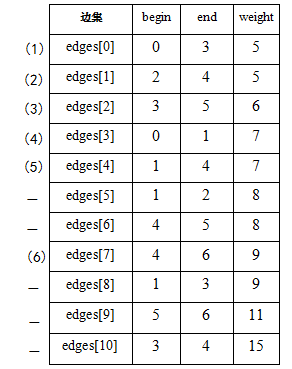
图解过程:原图如下 边集数组按权值顺序排列

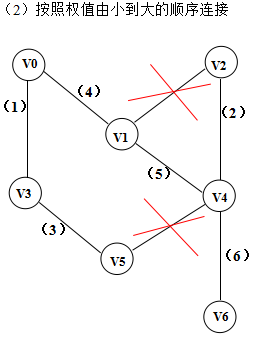
边<1, 2>和<4, 5>在添加到图中的时候形成了环,所以不能将v1和v2连起来。
第(6)条边之后整个图的顶点构成一棵树,所以加任何一条边都会成环,不在图中演示。
判断是否成环
代码:
参考资料:《大话数据结构》,《啊哈算法》,百度百科
基本思想:(1)构造一个只含n个顶点,边集为空的子图。若将图中各个顶点看成一棵树的根节点,则它是一个含有n棵树的森林。(2)从网的边集 E 中选取一条权值最小的边,若该条边的两个顶点分属不同的树,则将其加入子图。也就是说,将这两个顶点分别所在的两棵树合成一棵树;反之,若该条边的两个顶点已落在同一棵树上,则不可取,而应该取下一条权值最小的边再试之(3)依次类推,直至森林中只有一棵树,也即子图中含有 n-1条边为止。
大白话:(1)将图中的所有边都去掉。(2)将边按权值从小到大的顺序添加到图中,保证添加的过程中不会形成环(3)重复上一步直到连接所有顶点,此时就生成了最小生成树。这是一种贪心策略。
难点:判断某条边<u, v>的加入是否会在已经选定的边集集合中形成环。
解决办法:使用并查集,分别找出两个顶点u, v所在树的根节点。若根节点相同,说明u, v在同一棵树中,则u, v连接起来会形成环;若根节点不同,则u, v不在一棵树中,连接起来不会形成环,而是将两棵树合并。
图解过程:原图如下 边集数组按权值顺序排列




边<1, 2>和<4, 5>在添加到图中的时候形成了环,所以不能将v1和v2连起来。
第(6)条边之后整个图的顶点构成一棵树,所以加任何一条边都会成环,不在图中演示。
判断是否成环
int Find(int *parent, int f) {
while ( parent[f] > 0) {
f = parent[f];
}
return f;
}for (i = 0; i < G.numEdges; i++) {
n = Find(parent, edges[i].begin);//寻找边edge[i]的“首节点”所在树的树根
m = Find(parent, edges[i].end);//寻找边edge[i]的“尾节点”所在树的树根
//假如n与m不等,说明两个顶点不在一棵树内,因此这条边的加入不会使已经选择的边集产生回路
if (n != m) {
parent
= m;
printf("(%d, %d) %d\n", edges[i].begin, edges[i].end, edges[i].weight);
}
}代码:
//克鲁斯卡尔算法
//在连通网中求出最小生成树
#include <stdio.h>
#include <stdlib.h>
#define MAXEDGE 20
#define MAXVEX 20
#define INFINITY 65535
typedef struct
{
int arc[MAXVEX][MAXVEX];
int numVertexes, numEdges;//顶点数,边数
}MGraph;
typedef struct
{
int begin;
int end;
int weight;
}Edge; //对边集数组Edge结构的定义
//创建图的邻接矩阵
void CreateMGraph(MGraph *G) {
int i, j;
G->numEdges=11;
G->numVertexes=7;
for (i = 0; i < G->numVertexes; i++) {
for ( j = 0; j < G->numVertexes; j++) {
if (i==j)
G->arc[i][j]=0;
else
G->arc[i][j] = G->arc[j][i] = INFINITY;
}
}
G->arc[0][1]=7;
G->arc[0][3]=5;
G->arc[1][2]=8;
G->arc[1][3]=9;
G->arc[1][4]=7;
G->arc[2][4]=5;
G->arc[3][4]=15;
G->arc[3][5]=6;
G->arc[4][5]=8;
G->arc[4][6]=9;
G->arc[5][6]=11;
for(i = 0; i < G->numVertexes; i++) {
for(j = i; j < G->numVertexes; j++) {
G->arc[j][i] =G->arc[i][j];
}
}
}
//快速排序的条件
int cmp(const void* a, const void* b) {
return (*(Edge*)a).weight - (*(Edge*)b).weight;
}
//找到根节点
int Find(int *parent, int f) { while ( parent[f] > 0) { f = parent[f]; } return f; }
// 生成最小生成树
void MiniSpanTree_Kruskal(MGraph G) {
int i, j, n, m;
int k = 0;
int parent[MAXVEX]; //用于寻找根节点的数组
Edge edges[MAXEDGE]; //定义边集数组,edge的结构为begin,end,weight,均为整型
// 用来构建边集数组并排序(将邻接矩阵的对角线右边的部分存入边集数组中)
for ( i = 0; i < G.numVertexes-1; i++) {
for (j = i + 1; j < G.numVertexes; j++) {
if (G.arc[i][j] < INFINITY) {
edges[k].begin = i; //编号较小的结点为首
edges[k].end = j; //编号较大的结点为尾
edges[k].weight = G.arc[i][j];
k++;
}
}
}
//为边集数组Edge排序
qsort(edges, G.numEdges, sizeof(Edge), cmp);
for (i = 0; i < G.numVertexes; i++)
parent[i] = 0;
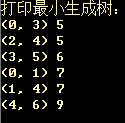
printf("打印最小生成树:\n");
for (i = 0; i < G.numEdges; i++) {
n = Find(parent, edges[i].begin);//寻找边edge[i]的“首节点”所在树的树根
m = Find(parent, edges[i].end);//寻找边edge[i]的“尾节点”所在树的树根
//假如n与m不等,说明两个顶点不在一棵树内,因此这条边的加入不会使已经选择的边集产生回路
if (n != m) {
parent
= m;
printf("(%d, %d) %d\n", edges[i].begin, edges[i].end, edges[i].weight);
}
}
}
int main(void)
{
MGraph G;
CreateMGraph(&G);
MiniSpanTree_Kruskal(G);
return 0;
}

相关文章推荐
- 交叉验证(Cross Validation)方法思想简介
- C++Builder 自定义消息 处理
- 阿里云服务器搭建之绑定多个域名
- Java语法基础思维图
- 【openjudge】开餐馆
- 友盟分享
- HPU 问题 H: 感恩节KK专场——陪学妹上课【规律】
- Ubuntu15.10 安装MySQL 5.7.9
- AndroidStudio怎么将开源项目发布到jcenter
- uva1585 Score
- @ModelAttribute运用详解
- Tesseract-OCR引擎 入门
- 阿里云服务器搭建之绑定多个域名
- 第一篇记录:
- 关于U-boot的移植(一)
- 心之所向,素履以往
- 网络编程
- 存储5——逻辑卷管理LVM
- hive中遇到的几个问题
- HPU 问题 G: 感恩节KK专场——与学妹滑雪 【最短路 double 精度判断】
