叉积
2015-11-19 14:54
204 查看
多维度的叉积涉及到的知识似乎没学过,而且似乎也暂时没有用,所以可以先只管二维与三维的情形。以下是知乎的相关问题的链接,下面有一些人的回答:
N维向量的叉积是如何被定义的
维基百科:向量积
两个向量

和

的叉积写作

×

(有时也被写成

∧

,避免和字母x混淆)。叉积可以定义为:

在这里θ表示

和

之间的角度(0°≤θ≤180°),它位于这两个矢量所定义的平面上。而
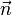
是一个与

、

所构成的平面垂直的单位矢量。
这个定义有个问题,就是同时有两个单位向量都垂直于

和

:若
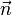
满足垂直的条件,那么-
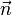
也满足。
“正确”的向量由向量空间的方向确定,即按照给定直角坐标系(
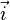
,
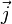
,
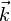
)的左右手定则。若
(
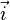
,
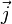
,
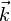
)满足右手定则,则
(

,

,

×

)也满足右手定则;或者两者同时满足左手定则。
一个简单的确定满足“右手定则”的结果向量的方向的方法是这样的:若坐标系是满足右手定则的,

当右手的四指从

以不超过180度的转角转向

时,竖起的大拇指指向是

的方向。由于向量的叉积由坐标系确定,所以其结果被称为伪向量。
叉积的模(长度)

可以解释成以

和

为边的平行四边形的面积。进一步就是说,混合积可以得到以

,

,

为边的平行六面体的体积。
反交换律:
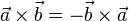
加法的分配律:

×
(

+

)
=

×

+

×

与标量乘法兼容:
(r

)
×

=

×
(r

) = r(

×

)不满足结合律,但满足雅可比(Jacobi)恒等式:

×
(

×

)
+

× (

×

)
+

× (

×

)
= 0
分配律,线性性和雅可比恒等式别表明:具有向量加法和叉积的R3构成了一个李代数。
两个非零向量

和

平行,当且仅当

×

= 0
这是一个著名的公式,而且非常有用:

×
(

×

)
=

(

·

)-

(

·

),
另一个有用的拉格朗日恒等式是:

。
这是一个在四元数代数中范数乘法

的特殊情形
给定直角坐标系的单位向量
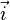
,
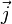
,
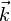
满足下列等式:

、

、

通过这些规则,两个向量的叉积的坐标可以方便地计算出来,不需要考虑任何角度:设


则

叉积也可以用四元数来表示。注意到上述
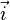
,
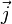
,
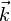
之间的叉积满足四元数的乘法。一般而言,若将向量[a1, a2, a3]表示成四元数a1i + a2j + a3k,两个向量的叉积可以这样计算:计算两个四元数的乘积得到一个四元数,并将这个四元数的实部去掉,即为结果。更多关于四元数乘法,向量运算及其几何意义请参见四元数与空间旋转。
计算公式的话:
三维:

二维: 二维的情形其实可以看作是三维的z=0的情形。所以公式就是上面的第三个部分 k的系数‘’
V1(x1, y1) X V2(x2, y2) = x1y2 – y1x2
点乘可以判断夹角的大小,锐直钝
利用叉乘可以计算平行四边形面积、三角形面积,从而计算多边形面积。还能根据正负计算左右位置关系。
这个网页里的可以帮助理解叉积:
高维空间的叉积及其几何意义
N维向量的叉积是如何被定义的
维基百科:向量积
两个向量

和

的叉积写作

×

(有时也被写成

∧

,避免和字母x混淆)。叉积可以定义为:

在这里θ表示

和

之间的角度(0°≤θ≤180°),它位于这两个矢量所定义的平面上。而
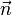
是一个与

、

所构成的平面垂直的单位矢量。
这个定义有个问题,就是同时有两个单位向量都垂直于

和

:若
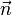
满足垂直的条件,那么-
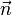
也满足。
“正确”的向量由向量空间的方向确定,即按照给定直角坐标系(
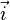
,
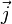
,
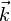
)的左右手定则。若
(
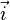
,
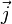
,
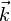
)满足右手定则,则
(

,

,

×

)也满足右手定则;或者两者同时满足左手定则。
一个简单的确定满足“右手定则”的结果向量的方向的方法是这样的:若坐标系是满足右手定则的,

当右手的四指从

以不超过180度的转角转向

时,竖起的大拇指指向是

的方向。由于向量的叉积由坐标系确定,所以其结果被称为伪向量。
几何意义[编辑]
叉积的模(长度) 
可以解释成以

和

为边的平行四边形的面积。进一步就是说,混合积可以得到以

,

,

为边的平行六面体的体积。
代数性质[编辑]
反交换律: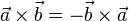
加法的分配律:

×
(

+

)
=

×

+

×

与标量乘法兼容:
(r

)
×

=

×
(r

) = r(

×

)不满足结合律,但满足雅可比(Jacobi)恒等式:

×
(

×

)
+

× (

×

)
+

× (

×

)
= 0
分配律,线性性和雅可比恒等式别表明:具有向量加法和叉积的R3构成了一个李代数。
两个非零向量

和

平行,当且仅当

×

= 0
拉格朗日公式[编辑]
这是一个著名的公式,而且非常有用:
×
(

×

)
=

(

·

)-

(

·

),
另一个有用的拉格朗日恒等式是:

。
这是一个在四元数代数中范数乘法

的特殊情形
矩阵形式[编辑]
给定直角坐标系的单位向量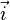
,
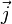
,
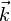
满足下列等式:

、

、

通过这些规则,两个向量的叉积的坐标可以方便地计算出来,不需要考虑任何角度:设


则

叉积也可以用四元数来表示。注意到上述
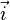
,
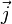
,
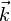
之间的叉积满足四元数的乘法。一般而言,若将向量[a1, a2, a3]表示成四元数a1i + a2j + a3k,两个向量的叉积可以这样计算:计算两个四元数的乘积得到一个四元数,并将这个四元数的实部去掉,即为结果。更多关于四元数乘法,向量运算及其几何意义请参见四元数与空间旋转。
计算公式的话:
三维:

二维: 二维的情形其实可以看作是三维的z=0的情形。所以公式就是上面的第三个部分 k的系数‘’
V1(x1, y1) X V2(x2, y2) = x1y2 – y1x2
点乘可以判断夹角的大小,锐直钝
利用叉乘可以计算平行四边形面积、三角形面积,从而计算多边形面积。还能根据正负计算左右位置关系。
这个网页里的可以帮助理解叉积:
高维空间的叉积及其几何意义
相关文章推荐
- 算法中的基础几何知识-叉积,线段,点
- Unity3D之Vector3.Dot和Vector3.Cross的使用
- Timus Online Judge 1966 Cycling Roads
- HDU2108-Shape of HDU
- POJ 2398(同POJ2318)
- hdu 2036 改革春风吹满地(叉积求多边形面积)
- poj 1696 Space Ant
- poj 2653 Pick-up sticks
- SSL 1720 Surround the Trees
- 专题:基础计算几何
- poj(2318)——TOYS(叉积的简单应用)
- POJ 1408-Fishnet(计算几何-根据交点求多边形面积)
- POJ1106(叉积应用)
- 叉积的性质 【poj2318】 TOYS
- 叉积(向量之间的计算)
- 【ZJU 1041 SSLGZ 1232】雷达覆盖
- 【HDU 2036】改革春风吹满地
- 【POJ 2606】Rabbit hunt
- 【SSLGZ 1579】泽泽在巴西
- (ssl1720)Surround the Trees(凸包问题,附带新手教程)
