prufer sequence

Prüfer sequence

From Wikipedia, the free encyclopedia

  (Redirected from Prufer sequence)


In combinatorial mathematics,
the Prüfer sequence (also Prüfer code or Prüfer numbers) of a labeled
tree is a unique sequence associated with the tree. The sequence for a tree on n vertices
has length n − 2, and can be generated by a simple iterative algorithm. Prüfer sequences were first used by Heinz
Prüfer to prove Cayley's formulain 1918.[1]

Contents

  [hide] 
1Algorithm
to convert a tree into a Prüfer sequence
1.1Example

2Algorithm
to convert a Prüfer sequence into a tree
3Cayley's
formula
4Other
applications[3]
5References
6External
links

Algorithm to convert a tree into a Prüfer sequence[edit]

One can generate a labeled tree's Prüfer sequence by iteratively removing vertices from the tree until only two vertices remain. Specifically, consider a labeled tree Twith vertices
{1, 2, ..., n}. At step i, remove the leaf with the smallest label and set the ith element of the Prüfer sequence to be the label of this leaf's neighbour.
The Prüfer sequence of a labeled tree is unique and has length n − 2.

Example[edit]

A labeled tree with Prüfer sequence {4,4,4,5}.

Consider the above algorithm run on the tree shown to the right. Initially, vertex 1 is the leaf with the smallest label, so it is removed first and 4 is put in the Prüfer sequence. Vertices
2 and 3 are removed next, so 4 is added twice more. Vertex 4 is now a leaf and has the smallest label, so it is removed and we append 5 to the sequence. We are left with only two vertices, so we stop. The tree's sequence is {4,4,4,5}.

Algorithm to convert a Prüfer sequence into a tree[edit]

Let 

{a[1], a[2], ..., a
}

 be a Prüfer
sequence:
The tree will have 

n+2

 nodes, numbered
from 

1

 to 

n+2

.
For each node set its degree to the number of times it appears in the sequence plus 1. For instance, in pseudo-code:

Convert-Prüfer-to-Tree(a)
1 n ← length[a]
2 T ← a graph with n + 2 isolated nodes, numbered 1 to n + 2
3 degree ← an array of integers
4 for each node i in T
5     do degree[i] ← 1
6 for each value i in a
7     do degree[i] ← degree[i] + 1

Next, for each number in the sequence 

a[i]

,
find the first (lowest-numbered) node, 

j

, with degree equal to 1, add the edge 

(j,
a[i])

 to the tree, and decrement the degrees of 

j

 and 

a[i]

.
In pseudo-code:

8 for each value i in a
9     for each node j in T
10          if degree[j] = 1
11             then Insert edge[i, j] into T
12                  degree[i] ← degree[i] - 1
13                  degree[j] ← degree[j] - 1
14                  break

At the end of this loop two nodes with degree 1 will remain (call them 

u

, 

v

).
Lastly, add the edge 

(u,v)

 to the tree.[2]

14 u ← v ← 0
15 for each node i in T
16     if degree[i] = 1
17         then if u = 0
18             then u ← i
19             else v ← i
20                  break
21 Insert edge[u, v] into T
22 degree[u] ← degree[u] - 1
23 degree[v] ← degree[v] - 1
24 return T

Cayley's formula[edit]

The Prüfer sequence of a labeled tree on n vertices is a unique sequence of length n − 2 on the labels 1 to n — this much is clear. Somewhat less obvious is the
fact that for a given sequence S of length n–2 on the labels 1 to n, there is a unique labeled tree whose Prüfer sequence is S.
The immediate consequence is that Prüfer sequences provide a bijection between
the set of labeled trees on n vertices and the set of sequences of length n–2 on the labels 1 to n. The latter set has size nn−2, so the existence of this bijection
proves Cayley's formula, i.e. that there are nn−2 labeled
trees on n vertices.

Other applications[3][edit]

Cayley's formula can be strengthened to prove the following claim:

The number of spanning trees in a complete graph 

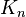
 with
a degree 

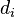
 specified for each vertex 

 is
equal to the multinomial coefficient


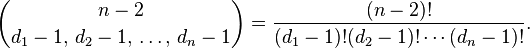
The proof follows by observing that in the Prüfer sequence number 

 appears
exactly 

 times.Cayley's formula can be generalized: a labeled tree is in fact a spanning
tree of the labeled complete graph. By placing restrictions on the enumerated Prüfer sequences,
similar methods can give the number of spanning trees of a complete bipartite graph. If G is
the complete bipartite graph with vertices 1 to n1 in one partition and vertices n1 + 1 to n in the other partition, the number of
labeled spanning trees of G is 

,
where n2 = n − n1.
Generating uniformly distributed random Prüfer sequences and converting them into the corresponding trees is a straightforward method of generating uniformly distributed random labelled trees.

以上内容摘自维基百科，大意是（n-2）长度的prufer sequence能表示n个节点的树，转化方法如下，对一棵树，先把树的叶子节点中标号最小的点摘除，把他的父亲放在数列中，重复此操作，直至树只剩两个节点，attention 根不是叶子节点，反过来，对于一个数列，将其未出现在数列中的最小标号的节点作为数列首的儿子，删除数列首，重复操作，直至数列为空。可以证明，（n-2）长度的prufer
sequence与n个节点的树是一一对应的关系。



那么，n个节点的树最多为n^(n-2)，
应用
1我们可以通过生成一个序列来生成一棵树，不用写并查集之类的了，同时由前文可得，一个点出现了多少次就有多少个儿子（除了根），那么我们就可以生成一个有度数要求的树，同时如果题目给定度数要求树的数目，我们就可以

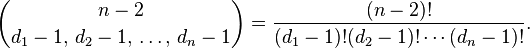
直接算了
2如果在一个完全二分图上求生成树，左边n1个点，右边n2个点，最后生成树的总数为