Lesson 6 Transposition and conjugation
2015-11-02 21:04
176 查看
The transpose

, conjugate

,
and adjoint (i.e., conjugate transpose)

of a matrix or vector

are
obtained by the member functions transpose(), conjugate(),
and adjoint(), respectively.
For real matrices,
As for basic arithmetic operators,
is written into
writing the result into
This is the so-called aliasing issue. In "debug mode", i.e., when assertions have
not been disabled, such common pitfalls are automatically detected.
For in-place transposition, as for instance in
There is also the adjointInPlace() function for complex
matrices.
The word adjoint has a number of related meanings. In linear algebra, it refers to the conjugate transpose and is most commonly
denoted
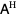

, conjugate

,
and adjoint (i.e., conjugate transpose)

of a matrix or vector

are
obtained by the member functions transpose(), conjugate(),
and adjoint(), respectively.
| Example: | Output: |
|---|---|
| MatrixXcf a = MatrixXcf::Random(2,2); cout << "Here is the matrix a\n" << a << endl; cout << "Here is the matrix a^T\n" << a.transpose() << endl; cout << "Here is the conjugate of a\n" << a.conjugate() << endl; cout << "Here is the matrix a^*\n" << a.adjoint() << endl; | Here is the matrix a (-0.211,0.68) (-0.605,0.823) (0.597,0.566) (0.536,-0.33) Here is the matrix a^T (-0.211,0.68) (0.597,0.566) (-0.605,0.823) (0.536,-0.33) Here is the conjugate of a (-0.211,-0.68) (-0.605,-0.823) (0.597,-0.566) (0.536,0.33) Here is the matrix a^* (-0.211,-0.68) (0.597,-0.566) (-0.605,-0.823) (0.536,0.33) |
conjugate()is a no-operation, and so
adjoint()is equivalent to
transpose().
As for basic arithmetic operators,
transpose()and
adjoint()simply return a proxy object without doing the actual transposition. If you do
b = a.transpose(), then the transpose is evaluated at the same time as the result
is written into
b. However, there is a complication here. If you do
a = a.transpose(), then Eigen starts
writing the result into
abefore the evaluation of the transpose is finished. Therefore, the instruction
a = a.transpose()does not replace
awith its transpose, as one would expect:
| Example: | Output: |
|---|---|
| Matrix2i a; a << 1, 2, 3, 4; cout << "Here is the matrix a:\n" << a << endl; a = a.transpose(); // !!! do NOT do this !!! cout << "and the result of the aliasing effect:\n" << a << endl; | Here is the matrix a: 1 2 3 4 and the result of the aliasing effect: 1 2 2 4 |
not been disabled, such common pitfalls are automatically detected.
For in-place transposition, as for instance in
a = a.transpose(), simply use the transposeInPlace() function:
| Example: | Output: |
|---|---|
| MatrixXf a(2,3); a << 1, 2, 3, 4, 5, 6; cout << "Here is the initial matrix a:\n" << a << endl; a.transposeInPlace(); cout << "and after being transposed:\n" << a << endl; | Here is the initial matrix a: 1 2 3 4 5 6 and after being transposed: 1 4 2 5 3 6 |
matrices.
The word adjoint has a number of related meanings. In linear algebra, it refers to the conjugate transpose and is most commonly
denoted
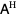
相关文章推荐
- POJ 2155 Matrix
- mysql配置感悟
- PHP怎么与C语言通信
- scala使用redis client - Jedis
- OC第五天之 Dictionary NSSet 数组排序
- sapi_module_struct 研究(一)
- 【LeetCode从零单刷】House Robber
- RCNN 安装编译与MATLAB2014下问题解决
- C#编程练习
- hdu 5532 Almost Sorted Array
- win7系统电脑机箱异常问题的解决方法
- 一次快速排序错误引发的思考
- 求排列的逆序数<归并><C++>
- listview 加载网络图片 item中上下有留白现象
- C/C++高阶语法:函数指针及其应用
- SELECTOR
- 软件文档的概念和细分
- TCP/IP实现以及常见问题
- 小电梯,学问大
- linux 基本操作笔记
