动态规划之矩阵连乘问题
2015-10-08 08:40
239 查看
A,动态规划:动态规划技术主要用于求解优化(optimization)问题,在优化问题中希望找出求解问题的“最佳”方式,但是这些求解的方式常常是指数级的。
B,矩阵连乘是一个利用动态规划求解的例子。
问题描述:给定n个二维矩阵集合,希望计算矩阵乘积A=A1•A2•••An,由于矩阵相乘具有结合律,因此我们可以给等式右边适当的添加括号,改变相乘的顺序,从而使整个计算过程乘法次数最少。例如:设B是一个2x10的矩阵,C是一个10x50的矩阵,D是一个50x20的矩阵,计算B•(C•D)需要10*50*20+
2*10*20 = 10400次乘法运算,而计算(B•C)•D需要2*10*50 + 2*50*20 =3000次乘法运算,后面一种加括号方式显然比前一种更佳。所以我们需要找到一种最优的运算顺序,可以使计算量达到最小,且理论上一定存在这种运算顺序方式。对于这样一种问题,我们就可以利用动态规划方法求解。下面详细解释该算法。
C,算法原理:
1)某个问题的最优解可以根据它的子问题的最优解定义;
2)我们对A1A2A3...An的子表达式Ai......Aj加括号,它一定具有(Ai...Ak)(Ak+1...Aj)这样的加括号形式,使得(Ai...Ak)和(Ak+1)均具有最优解,设Ni,j表示运算子表达式Ai......Aj一共所需的最少乘法次数,则假设k处是字表达式最佳加括号的位置,则 :


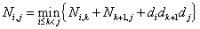
对于k的每个取值,计算相应的每个字表达式所需的乘法次数,再加上进行最后一次矩阵相乘(即子表达式(Ai...Ak)的结果矩阵与子表达式(Ak+1...Aj)的结果矩阵进行最后一次相乘)所需的乘法次数,对于每个字表达式Ai......Aj,选择使Ni,j值最小的k值作为s[i][j]的结果,其中s[i][j]表示k在字表达式Ai......Aj中的位置;
3)由于我们从N1,1开始计算然后依次计算N1,2,N2,3,N3,4....如下图所示:
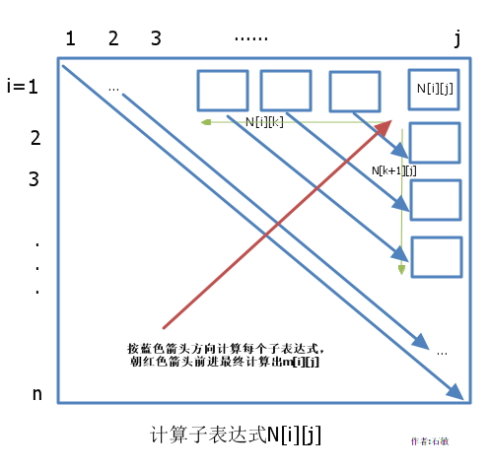

当计算N[i][j]的值得时候,N[i][k]和N[k+1][j]的值都已经计算出来,其中i<=k<=j;
D,算法实现:
#include "iostream"
using namespace std;
#define SIZE 50
int main()
{
void matrixChain(int[], int, int[][SIZE], int[][SIZE]);
void traceBack(int, int, int[][SIZE]);
int P[] = {12,23,7,40,21,16,34,10,31,17};
int n = sizeof(P)/sizeof(int*) - 1;
int N[SIZE][SIZE], K[SIZE][SIZE];
matrixChain(P, n, N, K);
traceBack(1, n, K);
cout<<"\n计算矩阵序列相乘一共需要乘法运算次数为:"<<N[1]
<<endl;
return 0;
}
//矩阵连乘算法
//P表示待计算矩阵序列,n表示矩阵个数,N表示i到j的子表达式的最优连乘次数,
//K表示i到j的字表达式添加括号的最佳位置
void matrixChain(int P[],int n ,int N[][SIZE], intK[][SIZE])
{
for(int i = 1; i <= n;++i)//N[i][i]表示只有一个矩阵,即第一条蓝色对角线均为0
N[i][i] = 0;
for(int r = 2; r <= n;r++)//每一条蓝色对角是一次循环,直到N[i][j]的那一条,朝红色线方向前进
for(int i = 1; i <= n-r+1; ++i)//对应于r值的对角线有n-r+1个元素
{
int j = r+i-1;//元素对应的列
N[i][j] = N[i][i] + N[i+1][j] +P[i-1]*P[i]*P[j];//此处k=i,即我们先假设在第一个位置切开
K[i][j] = i;
//下面循环k从i+1到j-1寻找使N[i][j]最小的k值
for(int k = i+1; k <= j-1; ++k)
{
int temp = N[i][k] + N[k+1][j] + P[i-1]*P[k]*P[j];
if(temp < N[i][j])
{
N[i][j] = temp;
K[i][j] = k;
}
}
}
}
//递归输出K中记录的位置
void traceBack(int i, int j, int K[][SIZE])
{
if(i == j)
{
cout<<"A"<<i;
return;
}
cout<<"(";
traceBack(i, K[i][j], K);
cout<<",";
traceBack(K[i][j]+1, j, K);
cout<<")";
}
运行结果:


E,复杂度分析
时间复杂度:程序中用了两个嵌套循环,时间复杂度为O(n^3)。
B,矩阵连乘是一个利用动态规划求解的例子。
问题描述:给定n个二维矩阵集合,希望计算矩阵乘积A=A1•A2•••An,由于矩阵相乘具有结合律,因此我们可以给等式右边适当的添加括号,改变相乘的顺序,从而使整个计算过程乘法次数最少。例如:设B是一个2x10的矩阵,C是一个10x50的矩阵,D是一个50x20的矩阵,计算B•(C•D)需要10*50*20+
2*10*20 = 10400次乘法运算,而计算(B•C)•D需要2*10*50 + 2*50*20 =3000次乘法运算,后面一种加括号方式显然比前一种更佳。所以我们需要找到一种最优的运算顺序,可以使计算量达到最小,且理论上一定存在这种运算顺序方式。对于这样一种问题,我们就可以利用动态规划方法求解。下面详细解释该算法。
C,算法原理:
1)某个问题的最优解可以根据它的子问题的最优解定义;
2)我们对A1A2A3...An的子表达式Ai......Aj加括号,它一定具有(Ai...Ak)(Ak+1...Aj)这样的加括号形式,使得(Ai...Ak)和(Ak+1)均具有最优解,设Ni,j表示运算子表达式Ai......Aj一共所需的最少乘法次数,则假设k处是字表达式最佳加括号的位置,则 :


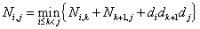
对于k的每个取值,计算相应的每个字表达式所需的乘法次数,再加上进行最后一次矩阵相乘(即子表达式(Ai...Ak)的结果矩阵与子表达式(Ak+1...Aj)的结果矩阵进行最后一次相乘)所需的乘法次数,对于每个字表达式Ai......Aj,选择使Ni,j值最小的k值作为s[i][j]的结果,其中s[i][j]表示k在字表达式Ai......Aj中的位置;
3)由于我们从N1,1开始计算然后依次计算N1,2,N2,3,N3,4....如下图所示:


当计算N[i][j]的值得时候,N[i][k]和N[k+1][j]的值都已经计算出来,其中i<=k<=j;
D,算法实现:
#include "iostream"
using namespace std;
#define SIZE 50
int main()
{
void matrixChain(int[], int, int[][SIZE], int[][SIZE]);
void traceBack(int, int, int[][SIZE]);
int P[] = {12,23,7,40,21,16,34,10,31,17};
int n = sizeof(P)/sizeof(int*) - 1;
int N[SIZE][SIZE], K[SIZE][SIZE];
matrixChain(P, n, N, K);
traceBack(1, n, K);
cout<<"\n计算矩阵序列相乘一共需要乘法运算次数为:"<<N[1]
<<endl;
return 0;
}
//矩阵连乘算法
//P表示待计算矩阵序列,n表示矩阵个数,N表示i到j的子表达式的最优连乘次数,
//K表示i到j的字表达式添加括号的最佳位置
void matrixChain(int P[],int n ,int N[][SIZE], intK[][SIZE])
{
for(int i = 1; i <= n;++i)//N[i][i]表示只有一个矩阵,即第一条蓝色对角线均为0
N[i][i] = 0;
for(int r = 2; r <= n;r++)//每一条蓝色对角是一次循环,直到N[i][j]的那一条,朝红色线方向前进
for(int i = 1; i <= n-r+1; ++i)//对应于r值的对角线有n-r+1个元素
{
int j = r+i-1;//元素对应的列
N[i][j] = N[i][i] + N[i+1][j] +P[i-1]*P[i]*P[j];//此处k=i,即我们先假设在第一个位置切开
K[i][j] = i;
//下面循环k从i+1到j-1寻找使N[i][j]最小的k值
for(int k = i+1; k <= j-1; ++k)
{
int temp = N[i][k] + N[k+1][j] + P[i-1]*P[k]*P[j];
if(temp < N[i][j])
{
N[i][j] = temp;
K[i][j] = k;
}
}
}
}
//递归输出K中记录的位置
void traceBack(int i, int j, int K[][SIZE])
{
if(i == j)
{
cout<<"A"<<i;
return;
}
cout<<"(";
traceBack(i, K[i][j], K);
cout<<",";
traceBack(K[i][j]+1, j, K);
cout<<")";
}
运行结果:


E,复杂度分析
时间复杂度:程序中用了两个嵌套循环,时间复杂度为O(n^3)。
