学习日志---图之最小生成树算法
2015-09-09 09:52
666 查看
最小生成树:
从最小生成树的定义可知,构造有n个结点的无向连通带权图的最小生成树,必须满足以下三条:
(1)构造的最小生成树必须包括n个结点;
(2)构造的最小生成树中有且只有n-1条边;
(3)构造的最小生成树中不存在回路。
构造最小生成树的方法有许多种,典型的构造方法有两种,一种称作普里姆(Prim)算法,另一种称作克鲁斯卡尔(Kruskal)算法。
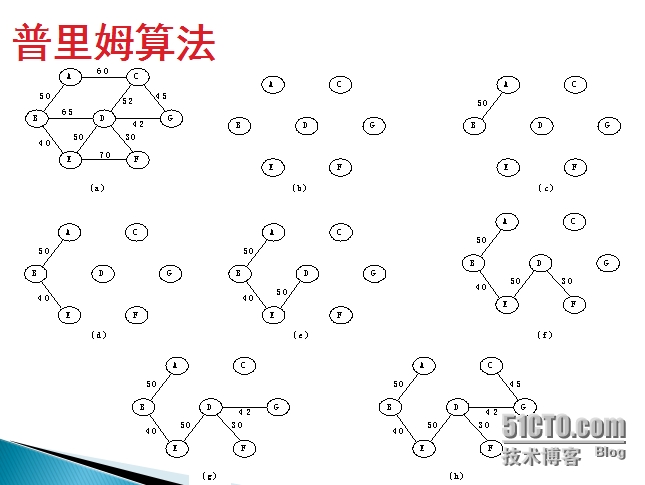
[b]特里姆算法[/b]
假设G=(V,E)为一个带权图,其中V为带权图中结点的集合,E为带权图中边的权值集合。设置两个新的集合U和T,其中U用于存放带权图G的最小生成树的结点的集合,T用于存放带权图G的最小生成树的权值的集合。
普里姆算法思想是:令集合U的初值为U={u0}(即假设构造最小生成树时从结点u0开始),集合T的初值为T={}。从所有结点u∈U和结点v∈V-U的带权边中选出具有最小权值的边(u,v),将结点v加入集合U中,将边(u,v) 加入集合T中。如此不断重复,当U=V时则最小生成树构造完毕。此时集合U中存放着最小生成树结点的集合,集合T中存放着最小生成树边的权值集合。
依然使用上次图的邻接矩阵,这里略
程序结果:
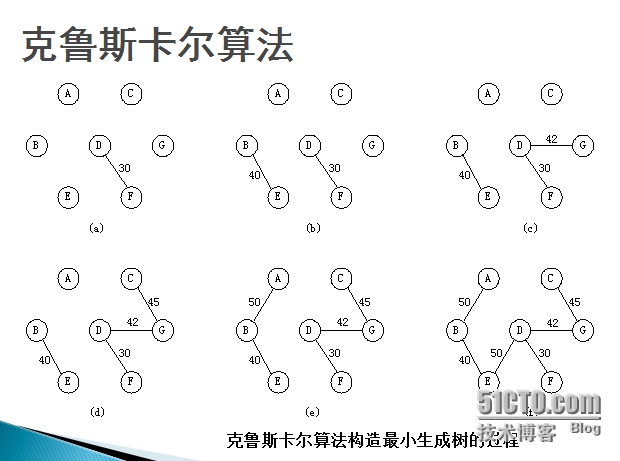
克鲁斯卡尔算法
由权值最小的边开始,不循环的找出最小的
克鲁斯卡尔算法是:设无向连通带权图G=(V,E),其中V为结点的集合,E为边的集合。设带权图G的最小生成树T由结点集合和边的集合构成,其初值为T=(V,{}),即初始时最小生成树T只由带权图G中的结点集合组成,各结点之间没有一条边。这样,最小生成树T中的各个结点各自构成一个连通分量。然后,按照边的权值递增的顺序考察带权图G中的边集合E中的各条边。若被考察的边的两个结点属于T的两个不同的连通分量,则将此边加入到最小生成树T,同时把两个连通分量连接为一个连通分量;若被考察的边的两个结点属于T的同一个连通分量,则将此边舍去。如此下去,当T中的连通分量个数为1时,T中的该连通分量即为带权图G的一棵最小生成树。
代码来源github: https://github.com/wangkuiwu/datastructs_and_algorithm/blob/master/source/graph/kruskal/udg/java/MatrixUDG.java
从最小生成树的定义可知,构造有n个结点的无向连通带权图的最小生成树,必须满足以下三条:
(1)构造的最小生成树必须包括n个结点;
(2)构造的最小生成树中有且只有n-1条边;
(3)构造的最小生成树中不存在回路。
构造最小生成树的方法有许多种,典型的构造方法有两种,一种称作普里姆(Prim)算法,另一种称作克鲁斯卡尔(Kruskal)算法。
[b]特里姆算法[/b]
假设G=(V,E)为一个带权图,其中V为带权图中结点的集合,E为带权图中边的权值集合。设置两个新的集合U和T,其中U用于存放带权图G的最小生成树的结点的集合,T用于存放带权图G的最小生成树的权值的集合。
普里姆算法思想是:令集合U的初值为U={u0}(即假设构造最小生成树时从结点u0开始),集合T的初值为T={}。从所有结点u∈U和结点v∈V-U的带权边中选出具有最小权值的边(u,v),将结点v加入集合U中,将边(u,v) 加入集合T中。如此不断重复,当U=V时则最小生成树构造完毕。此时集合U中存放着最小生成树结点的集合,集合T中存放着最小生成树边的权值集合。
依然使用上次图的邻接矩阵,这里略
//这个类存放了最小生成树的节点和路过所需的权值
public class MinSpanTree {
Object vertex;
int weight;
MinSpanTree()
{
}
MinSpanTree(Object obj,int weight)
{
this.vertex = obj;
this.weight = weight;
}
}特里姆算法类public class Prim {
public final static int MAXWEIGHT = 9999;
//特里姆算法
public static void prim(MyAdjGraphic g,MinSpanTree[] closeVertex) throws Exception
{
int n = g.getNumOfVertice(); //获得结点数量
//lowcost要反复使用,表示当前节点与其他节点之间的权值
int[] lowCost = new int
;
int k=0;
int minCost;
//初始化closeVertex数组
//以0作为起点开始建立最小生成树
for(int i=0;i<n;i++)
{
lowCost[i] = g.getWeightOfEdges(0, i);
}
MinSpanTree temp = new MinSpanTree();
temp.vertex = g.getValueOfVertice(0);
closeVertex[0] = temp;
lowCost[0] = - 2;//标记为已访问
//上面是初始化,选择起点,下面是对后面n-1个节点进行选择
for(int i = 1; i < n; i ++)
{
minCost = MAXWEIGHT;
//从lowcost里面选择当前最小权重的路径
//lowcost的下标对应的是节点位置
for(int j = 1; j < n; j ++)
{
if(lowCost[j] < minCost && lowCost[j] > 0)
{
minCost = lowCost[j];
//设置k为当前最小权重的节点
k = j;
}
}
//建立选择的路径对象,并把该路径设置为访问过
MinSpanTree curr = new MinSpanTree();
curr.vertex = g.getValueOfVertice(k);
curr.weight = minCost;
closeVertex[i] = curr;
lowCost[k] = -2; //标记为已访问
//对当前k节点,设置lowcost数组,对应每个节点的权重
for(int j = 1; j < n; j ++)
{
if(g.getWeightOfEdges(k, j)>0) //说明有边存在
{
if(lowCost[j]==-1)
{
lowCost[j] = g.getWeightOfEdges(k, j);
}
else
{
//保证其去到该点的权重最小,如还不如以前的小,则保留以前的
if(g.getWeightOfEdges(k, j)< lowCost[j]&& lowCost[j]!=-2)
{
lowCost[j] = g.getWeightOfEdges(k, j);
}
}
}
}
}
}
}测试类:public class Test {
static final int maxVertices = 100;
public static void main(String[] args) {
MyAdjGraphic g = new MyAdjGraphic(maxVertices);
Object[] vertices = {new Character('A'),new Character('B'),new Character('C'),
new Character('D'),new Character('E'),new Character('F'),new Character('G')};
Weight[] weight = {new Weight(0,1,50),new Weight(1,0,50),
new Weight(0,2,60),new Weight(2,0,60),new Weight(1,3,65),
new Weight(3,1,65),new Weight(1,4,40),new Weight(4,1,40),
new Weight(2,3,52),new Weight(3,2,52),new Weight(2,6,45),
new Weight(6,2,45),new Weight(3,4,50),new Weight(4,3,50),
new Weight(3,5,30),new Weight(5,3,30),new Weight(3,6,42),
new Weight(6,3,42),new Weight(4,5,70),new Weight(5,4,70)};
int n = 7, e = 20;
try
{
//这里建立的邻接矩阵就是下面的的图
Weight.createAdjGraphic(g, vertices, n, weight, e);
MinSpanTree[] closeVertex = new MinSpanTree[7];
Prim.prim(g, closeVertex);
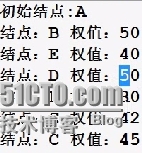
System.out.println("初始结点:"+closeVertex[0].vertex);
for(int i=1;i<n;i++)
{
System.out.println("结点:"+closeVertex[i].vertex+" 权值:"+closeVertex[i].weight);
}
}
catch(Exception ex)
{
}
}
}
程序结果:

克鲁斯卡尔算法
由权值最小的边开始,不循环的找出最小的
克鲁斯卡尔算法是:设无向连通带权图G=(V,E),其中V为结点的集合,E为边的集合。设带权图G的最小生成树T由结点集合和边的集合构成,其初值为T=(V,{}),即初始时最小生成树T只由带权图G中的结点集合组成,各结点之间没有一条边。这样,最小生成树T中的各个结点各自构成一个连通分量。然后,按照边的权值递增的顺序考察带权图G中的边集合E中的各条边。若被考察的边的两个结点属于T的两个不同的连通分量,则将此边加入到最小生成树T,同时把两个连通分量连接为一个连通分量;若被考察的边的两个结点属于T的同一个连通分量,则将此边舍去。如此下去,当T中的连通分量个数为1时,T中的该连通分量即为带权图G的一棵最小生成树。
代码来源github: https://github.com/wangkuiwu/datastructs_and_algorithm/blob/master/source/graph/kruskal/udg/java/MatrixUDG.java
克鲁斯卡尔(Kruskal)最小生成树
public void kruskal() {
int index = 0; // rets数组的索引
int[] vends = new int[mEdgNum]; // 用于保存"已有最小生成树"中每个顶点在该最小树中的终点。
EData[] rets = new EData[mEdgNum]; // 结果数组,保存kruskal最小生成树的边
EData[] edges; // 图对应的所有边
// 获取"图中所有的边"
edges = getEdges();
// 将边按照"权"的大小进行排序(从小到大)
sortEdges(edges, mEdgNum);
//核心代码
//从最轻的权重开始选择
for (int i=0; i<mEdgNum; i++) {
int p1 = getPosition(edges[i].start); // 获取第i条边的"起点"的序号
int p2 = getPosition(edges[i].end); // 获取第i条边的"终点"的序号
//在vends数组中找终点
int m = getEnd(vends, p1); // 获取p1在"已有的最小生成树"中的终点
int n = getEnd(vends, p2); // 获取p2在"已有的最小生成树"中的终点
// 如果m!=n,意味着"边i"与"已经添加到最小生成树中的顶点"没有形成环路
if (m != n) {
vends[m] = n; // 设置m在"已有的最小生成树"中的终点为n
rets[index++] = edges[i]; // 保存结果
}
}
// 统计并打印"kruskal最小生成树"的信息
int length = 0;
for (int i = 0; i < index; i++)
length += rets[i].weight;
System.out.printf("Kruskal=%d: ", length);
for (int i = 0; i < index; i++)
System.out.printf("(%c,%c) ", rets[i].start, rets[i].end);
System.out.printf("\n");
}
// 获取图中的边
private EData[] getEdges() {
int index=0;
EData[] edges;
edges = new EData[mEdgNum];
for (int i=0; i < mVexs.length; i++) {
for (int j=i+1; j < mVexs.length; j++) {
//这里获取的是邻接矩阵的上三角,可以保证节点之间的连线是单一的,不是混乱的
if (mMatrix[i][j]!=INF) {
edges[index++] = new EData(mVexs[i], mVexs[j], mMatrix[i][j]);
}
}
}
return edges;
}
// 对边按照权值大小进行排序(由小到大)
private void sortEdges(EData[] edges, int elen) {
for (int i=0; i<elen; i++) {
for (int j=i+1; j<elen; j++) {
if (edges[i].weight > edges[j].weight) {
// 交换"边i"和"边j"
EData tmp = edges[i];
edges[i] = edges[j];
edges[j] = tmp;
}
}
}
}
// 获取i的终点
// 这里vends是环装的结构,也就是邻接矩阵向右侧移动
private int getEnd(int[] vends, int i) {
while (vends[i] != 0)
i = vends[i];
return i;
}
// 边的结构体
private static class EData {
char start; // 边的起点
char end; // 边的终点
int weight; // 边的权重
public EData(char start, char end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
};
