二之再续、Dijkstra 算法+fibonacci堆的逐步c实现

原作者地址：http://blog.csdn.net/v_JULY_v/article/details/6259576



二之再续、Dijkstra 算法+fibonacci堆的逐步c实现

作者:JULY、二零一一年三月十八日

出处：http://blog.csdn.net/v_JULY_v

----------------------------------

引言：

来考虑一个问题，

平面上6个点，A,B,C,D,E,F，假定已知其中一些点之间的距离，

现在，要求A到其它5个点，B,C,D,E,F各点的最短距离。
如下图所示：



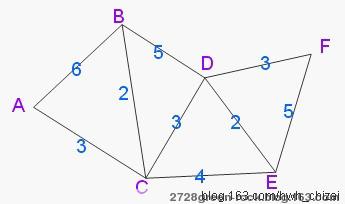
经过上图，我们可以轻而易举的得到A->B,C,D,E,F各点的最短距离：
目的 路径 最短距离

A=>A， A->A 0

A=>B， A->C->B 3+2=5

A=>C， A->C 3

A=>D， A->C->D 3+3=6

A=>E， A->C->E 3+4=7

A=>F， A->C->D->F 3+3+3=9
我想，如果是单单出上述一道填空题，要你答出A->B,C,D,E,F各点的最短距离，

一个小学生，掰掰手指，也能在几分钟之内，填写出来。
我们的问题，当然不是这么简单，上述只是一个具体化的例子而已。

实际上，很多的问题，如求图的最短路径问题，就要用到上述方法，不断比较、不断寻找，以期找到最短距离的路径，此类问题，便是Dijkstra 算法的应用了。当然，还有BFS算法，以及更高效的A*搜寻算法。
A*搜寻算法已在本BLOG内有所详细的介绍，本文咱们结合fibonacci堆实现Dijkstra 算法。

即，Dijkstra + fibonacci堆 c实现。
我想了下，把一个算法研究够透彻之后，还要编写代码去实现它，才叫真正掌握了一个算法。本BLOG内经典算法研究系列，已经写了18篇文章，十一个算法，所以，还有10多个算法，待我去实现。

代码风格

实现一个算法，首先要了解此算法的原理，了解此算法的原理之后，便是写代码实现。

在打开编译器之前，我先到网上搜索了一下“Dijkstra 算法+fibonacci堆实现”。
发现：网上竟没有过 Dijkstra + fibonacci堆实现的c代码，而且如果是以下几类的代码，我是直接跳过不看的：
1、没有注释(看不懂)。

2、没有排版(不舒服)。

3、冗余繁杂(看着烦躁)。

fibonacci堆实现Dijkstra 算法
ok，闲话少说，咱们切入正题。下面，咱们来一步一步利用fibonacci堆实现Dijkstra 算法吧。

前面说了，要实现一个算法，首先得明确其算法原理及思想，而要理解一个算法的原理，又得知道发明此算法的目的是什么，即，此算法是用来干什么的?
由前面的例子，我们可以总结出：Dijkstra 算法是为了解决一个点到其它点最短距离的问题。

我们总是要找源点到各个目标点的最短距离，在寻路过程中，如果新发现了一个新的点，发现当源点到达前一个目的点路径通过新发现的点时，路径可以缩短，那么我们就必须及时更新此最短距离。
ok，举个例子：如我们最初找到一条路径，A->B，这条路径的最短距离为6，后来找到了C点，发现若A->C->B点路径时，A->B的最短距离为5，小于之前找到的最短距离6，所以，便得此更新A到B的最短距离：为5，最短路径为A->C->B.
好的，明白了此算法是干什么的，那么咱们先用伪代码尝试写一下吧(有的人可能会说，不是吧，我现在，什么都还没搞懂，就要我写代码了。额，你手头不是有资料么，如果全部所有的工作，都要自己来做的话，那就是一个浩大的工程了。:D。)。
咱们先从算法导论上，找来Dijkstra 算法的伪代码如下：
DIJKSTRA(G, w, s)

1 INITIALIZE-SINGLE-SOURCE(G, s) //1、初始化结点工作

2 S ← Ø

3 Q ← V[G] //2、插入结点操作

4 while Q ≠ Ø

5 do u ← EXTRACT-MIN(Q) //3、从最小队列中，抽取最小点工作

6 S ← S ∪{u}

7 for each vertex v ∈ Adj[u]

8 do RELAX(u, v, w) //4、松弛操作。
伪代码毕竟与能在机子上编译运行的代码，还有很多工作要做。

首先，咱们看一下上述伪代码，可以看出，基本上，此Dijkstra 算法主要分为以下四个步骤：
1、初始化结点工作

2、插入结点操作

3、从最小队列中，抽取最小点工作

4、松弛操作。
ok，由于第2个操作涉及到斐波那契堆，比较复杂一点，咱们先来具体分析第1、2、4个操作：
1、得用O（V）的时间，来对最短路径的估计，和对前驱进行初始化工作。
INITIALIZE-SINGLE-SOURCE(G, s)

1 for each vertex v ∈ V[G]

2 do d[v] ← ∞

3 π[v] ← NIL //O（V）

4 d[s] 0
我们根据上述伪代码，不难写出以下的代码：
void init_single_source(Graph *G,int s)

{

for (int i=0;i<G->n;i++) {

d[i]=INF;

pre[i]=-1;

}

d[s]=0;

}
2、插入结点到队列的操作
2 S ← Ø

3 Q ← V[G] //2、插入结点操作
代码：

for (i=0;i<G->n;i++)

S[i]=0;
4、松弛操作。

首先得理解什么是松弛操作：

Dijkstra 算法使用了松弛技术，对每个顶点v<-V，都设置一个属性d[v]，用来描述从源点s到v的最短路径上权值的上界，称为最短路径的估计。

RELAX(u, v, w)

1 if d[v] > d[u] + w(u, v)

2 then d[v] ← d[u] + w(u, v)

3 π[v] ← u //O（E）
同样，我们不难写出下述代码：

void relax(int u,int v,Graph *G)

{

if (d[v]>d[u]+G->w[u][v])

{

d[v] = d[u]+G->w[u][v]; //更新此最短距离

pre[v]=u; //u为v的父结点

}

}
再解释一下上述relax的代码，其中u为v的父母结点，当发现其父结点d[u]加上经过路径的距离G->w[u][v]，小于子结点到源点的距离d[v]，便得更新此最短距离。

请注意，说的明白点：就是本来最初A到B的路径为A->B，现在发现，当A经过C到达B时，此路径距离比A->B更短，当然，便得更新此A到B的最短路径了，即是：A->C->B，C 即成为了B的父结点(如此解释，我相信您已经明朗。:D。)。

即A=>B <== A->C->B，执行赋值操作。
ok，第1、2、4个操作步骤，咱们都已经写代码实现了，那么，接下来，咱们来编写第3个操作的代码：3、从最小队列中，抽取最小点工作。
相信，你已经看出来了，我们需要构造一个最小优先队列，那用什么来构造最小优先队列列?对了，堆。什么堆最好，效率最高，呵呵，就是本文要实现的fibonacci堆。
为什么?ok，请看最小优先队列的三种实现方法比较：
EXTRACT-MIN + RELAX

I、 简单方式： O（V*V + E*1）

II、 二叉/项堆： O（V*lgV + |E|*lgV）

源点可达：O（E*lgV）

稀疏图时，有E=o（V^2/lgV），

=> O（V^2）

III、斐波那契堆：O（V*lgV + E）
其中，V为顶点，E为边。好的，这样我们就知道了：Dijkstra 算法中，当用斐波纳契堆作优先队列时，算法时间复杂度为O（V*lgV + E）。
额，那么接下来，咱们要做的是什么列?当然是要实现一个fibonacci堆了。可要怎么实现它，才能用到我们

Dijkstra 算法中列?对了，写成一个库的形式。库?呵呵，是一个类。
ok，以下就是这个fibonacci堆的实现：


//FibonacciHeap.h

#ifndef _FIBONACCI_HEAP_H_INCLUDED_

#define _FIBONACCI_HEAP_H_INCLUDED_



#include <functional>

#include <algorithm>



template<typename T>

struct Fib_node

{

Fib_node* ns_; //后驱结点

Fib_node *pt_; //父母结点

Fib_node* ps_; //前驱结点

Fib_node* fc_; //头结点

int rank_; //孩子结点

bool marked_; //孩子结点是否删除的标记

T* pv_;

Fib_node(T* pv = 0) : pv_(pv) { }

T& value(void) { return *pv_; }

void set_src(T* pv) { pv_ = pv; }

}; //Fib_node的数据结构





template<class Node, class OD>

Node* merge_tree(Node*a, Node* b, OD small) //合并结点

{

if(small(b->value(), a->value()))

swap(a, b);

Node* fc = a->fc_;

a->fc_ = b;

a->ns_ = a->ps_ = a->pt_ = 0;

++a->rank_;



b->pt_ = a; //a为b的父母

b->ns_ = fc; //第一个结点赋给b的前驱结点

b->ps_ = 0;

if(fc != 0)

fc->ps_ = b;

return a;

}



template<typename Node>

void erase_node(Node* me) //删除结点

{

Node* const p = me->pt_;

--p->rank_;

if(p->fc_ == me) //如果me是头结点

{

if((p->fc_ = me->ns_) != 0)

me->ns_->ps_ = 0;

}

else

{

Node *prev = me->ps_;

Node *next = me->ns_; //可能为0

prev->ns_ = next;

if(next != 0)

next->ps_ = prev;

}

}





template<class Node, class OD>

Node* merge_fib_heap(Node* a, Node* b, OD small) //调用上述的merge_tree合并fib_heap。

{

enum {SIZE = 64}; //

Node* v[SIZE] = {0};

int k;

while(a != 0)

{

Node* carry = a;

a = a->ns_;

for(k = carry->rank_; v[k] != 0; ++k)

{

carry = merge_tree(carry, v[k], small);

v[k] = 0;

}

v[k] = carry;

}

while(b != 0)

{

Node* carry = b;

b = b->ns_;

for(k = carry->rank_; v[k] != 0; ++k)

{

carry = merge_tree(carry, v[k], small);

v[k] = 0;

}

v[k] = carry;

}

Node** t = std::remove(v, v+SIZE, (Node*)0);

int const n = t - v;

if(n > 0)

{

for(k = 0; k < n - 1; ++k)

v[k]->ns_ = v[k+1];

for(k = 1; k < n; ++k)

v[k]->ps_ = v[k-1];

v[n-1]->ns_ = v[0]->ps_ = 0;

}

return v[0];

}



template<typename T, class OD = std::less<T> >

struct Min_fib_heap //抽取最小结点

{

typedef Fib_node<T> Node;

typedef Node Node_type;



Node* roots_;

Node* min_; //pointer to the minimum node

OD less_;



Min_fib_heap(void): roots_(0), min_(0), less_() { }

bool empty(void) const { return roots_ == 0; }

T& top(void) const { return min_->value(); }



void decrease_key(Node* me) //删除

{ //precondition: root_ not zero

if(less_(me->value(), min_->value()))

min_ = me;

cascading_cut(me);

}

void push(Node* me) //压入

{

me->pt_ = me->fc_ = 0;

me->rank_ = 0;

if(roots_ == 0)

{

me->ns_ = me->ps_ = 0;

me->marked_ = false;

roots_ = min_ = me;

}

else

{

if(less_(me->value(), min_->value()))

min_ = me;

insert2roots(me);

}

}

Node* pop(void) //弹出

{

Node* const om = min_;

erase_tree(min_);

min_ = roots_ = merge_fib_heap(roots_, min_->fc_, less_);

if(roots_ != 0) //find new min_

{

for(Node* t = roots_->ns_; t != 0; t = t->ns_)

if(less_(t->value(), min_->value()))

min_ = t;

}

return om;

}

void merge(void) //合并

{

if(empty()) return;

min_ = roots_ = merge_fib_heap(roots_, (Node*)0, less_);

for(Node* a = roots_->ns_; a != 0; a = a->ns_)

if(less_(a->value(), min_->value() ))

min_ = a;

}

private:

void insert2roots(Node* me) //插入

{ //precondition: 1) root_ != 0; 2) me->value() >= min_->value()

me->pt_ = me->ps_ = 0;

me->ns_ = roots_;

me->marked_ = false;

roots_->ps_ = me;

roots_ = me;

}

void cascading_cut(Node* me) //断开

{ //precondition: me is not a root. that is me->pt_ != 0

for(Node* p = me->pt_; p != 0; me = p, p = p->pt_)

{

erase_node(me);

insert2roots(me);

if(p->marked_ == false)

{

p->marked_ = true;

break;

}

}

}

void erase_tree(Node* me) //删除

{

if(roots_ == me)

{

roots_ = me->ns_;

if(roots_ != 0)

roots_->ps_ = 0;

}

else

{

Node* const prev = me->ps_;

Node* const next = me->ns_;

prev->ns_ = next;

if(next != 0)

next->ps_ = prev;

}

}

}; //Min_fib_heap的类





template<typename Fitr>

bool is_sorted(Fitr first, Fitr last)

{

if(first != last)

for(Fitr prev = first++; first != last; prev = first++)

if(*first < *prev) return false;

return true;

}

template<typename Fitr, class OD>

bool is_sorted(Fitr first, Fitr last, OD cmp)

{

if(first != last)

for(Fitr prev = first++; first != last; prev = first++)

if(cmp(*first, *prev)) return false;

return true;

}



由于本BLOG日后会具体阐述这个斐波那契堆的各项操作，限于篇幅，在此，就不再啰嗦解释上述程序了。
ok，实现了fibonacci堆，接下来，咱们可以写Dijkstra 算法的代码了。为了版述清晰，再一次贴一下此算法的伪代码：
DIJKSTRA(G, w, s)

1 INITIALIZE-SINGLE-SOURCE(G, s)

2 S ← Ø

3 Q ← V[G] //第3行，INSERT操作，O（1）

4 while Q ≠ Ø

5 do u ← EXTRACT-MIN(Q) //第5行，EXTRACT-MIN操作，V*lgV

6 S ← S ∪{u}

7 for each vertex v ∈ Adj[u]

8 do RELAX(u, v, w) //第8行，RELAX操作，E*O(1)
编写的Dijkstra算法的c代码如下：


void Dijkstra(int s, T d[], int p[])

{

//寻找从顶点s出发的最短路径,在d中存储的是s->i的最短距离

//p中存储的是i的父节点

if (s < 1 || s > n)

throw OutOfBounds();



//路径可到达的顶点列表,这里可以用上述实现的fibonacci堆代码。

Chain<int> L;



ChainIterator<int> I;

//初始化d, p, and L

for (int i = 1; i <= n; i++)

{

d[i] = a[s][i];



if (d[i] == NoEdge)

{

p[i] = 0;

}

else

{

p[i] = s;

L.Insert(0,i);

}

}



//更新d, p

while (!L.IsEmpty())

{

//寻找最小d的点v

int *v = I.Initialize(L);

int *w = I.Next();

while (w)

{

if (d[*w] < d[*v])

v = w;



w = I.Next();

}



int i = *v;

L.Delete(*v);

for (int j = 1; j <= n; j++)

{

if (a[i][j] != NoEdge

&& (!p[j] || d[j] > d[i] + a[i][j])) //d[i]是父节点

{

// 刷新更小的d[j]

d[j] = d[i] + a[i][j];



// 如果j没有父节点,则添加到L

if (!p[j])

L.Insert(0,j);



// 更新父节点

p[j] = i;

}

}

}

}



更好的代码，还在进一步修正中。日后，等完善好后，再发布整个工程出来。

下面是演示此Dijkstra算法的工程的俩张图（0为源点，4为目标点，第二幅图中的红色路径即为所求的0->4的最短距离的路径）：





完。