范数

1. 概念

一个矩阵 x 的 p 范数可以定义为：

||x||p=∑i|xi|p−−−−−−−√p

0 范数

表示非0元素的个数

1 范数

所有元素的绝对值的和：||x||1=∑i|xi|

2 范数

所有元素的平方和，然后开根号：||x||2=∑i|xi|2−−−−−−√

无穷范数

最大元素的绝对值

2. l0 范数

在压缩感知（compress sensing）理论中，要找到最稀疏的解（也就是有最少的非0元素个数的解），可以用下式表示：

min||x||0s.t.Ax=b

然而，我们不确定 x 中有几个非 0 元素，也不确定哪几个是非 0 元素，要想求解，每种情况都遍历一遍，这样的计算量是不可想象的，是一个 NP-hard 问题。

3. NP-hard 问题

什么是 NP-hard 问题呢，NP是指非确定性多项式。所谓非确定性多项式是指，可用一定数量的运算解决的多项式时间内可以解决的问题。最典型的 NP-hard 问题就是图论中的旅行、推销员问题：

已知一个 n 个点的完全图，每条边都有一个长度，求总长度最短的，经过每个点各一次的封闭回路。

必须检查所有的可行方案，才能确定当前解是否最优，这就是 NP-hard 问题。

4. l1 范数

l1 范数是 l0 范数（非凸）的最优凸近似，比 l0 范数更容易优化求解，所以可以将 l0 范数的优化转换为 l1 范数的优化：

min||x||0s.t.Ax=b在一定条件下<=========>概率意义下等价min||x||1s.t.Ax=b

上述式子中所述的

在一定条件下

，就是压缩感知理论中所说的：投影矩阵满足 RIP 性质的条件下。

5. 范数稀疏刻化

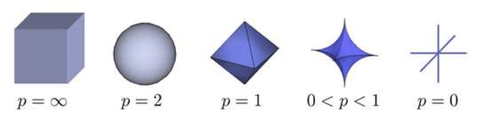
如上图所示，是不同范数的三维空间表示形式，0 范数表示坐标轴，1范数是锥体，2范数表示一个球体，从上图也可以看出，p < 1 时，p范数是非凸的，当 p >= 1 时，是凸的。



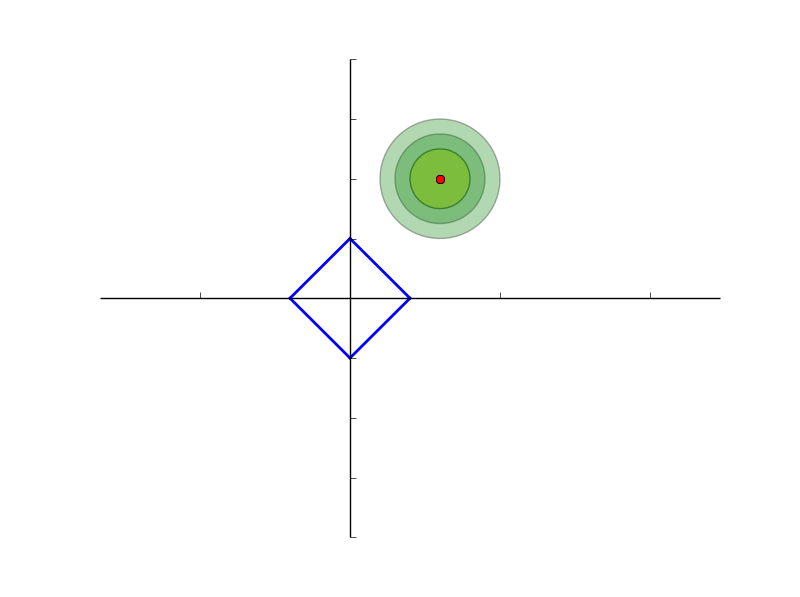
如上图所示，四边形表示 1 范数，圆环表示目标函数的等高线，目标函数很有可能与l1中的角点首先相交（在角点处相交就产生了稀疏性），而在l2中就没有角点，也就没有这样的特性。所以，通过 l1 范数约束可以求得稀疏解，而通过 l2 范数不能产生稀疏解。

那么为什么上图中等高线与角点相交的概率更高呢？看下图所示：



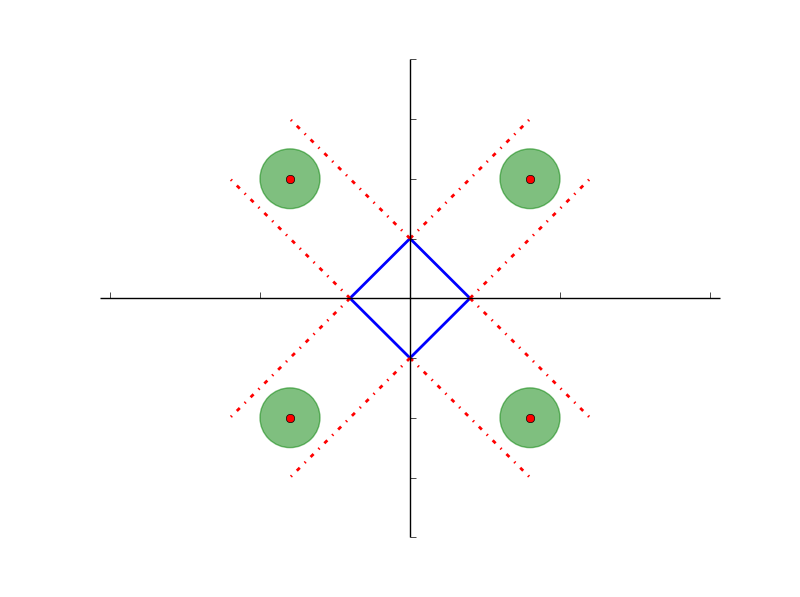
如果圆的中心位于上图所示的红色虚线包围的4个区域，那么等高线总会先于四边形的四个边相交，而如果圆心不在这四个区域，那么必定先于角点相交。而红色虚线包围的区域要远远小于除此之外的区域，所以，从概率上说，目标函数很可能与角点首先相交。

当然，对于 lp (0 < p < 1)，与角点相交的可能性就更大，所以比 l1 具有更好的稀疏刻画能力（但是非凸）。

稀疏刻化能力：l0>lp(0<p<1)>l1>l2