决策树ID3;C4.5详解和python实现与R语言实现比较
2014-12-24 22:22
821 查看
本文网址:http://blog.csdn.net/crystal_tyan/article/details/42130851(请不要在采集站阅读)
把决策树研究一下,找来了一些自己觉得还可以的资料:
分类树(决策树)是一种十分常用的分类方法。他是一种监管学习,所谓监管学习说白了很简单,就是给定一堆样本,每个样本都有一组属性和一个类别,这些类别是事先确定的,那么通过学习得到一个分类器,这个分类器能够对新出现的对象给出正确的分类。这样的机器学习就被称之为监督学习。分类本质上就是一个map的过程。C4.5分类树就是决策树算法中最流行的一种。下面给出一个数据集作为算法例子的基础,比如有这么一个数据集,如下:

这个Golf数据集就是我们这篇博客讨论的基础。我们分类的目的就是根据某一天的天气状态,如天气,温度,湿度,是否刮风,来判断这一天是否适合打高尔夫球。

上面的图片已经很明显得说明了决策树的原理了
下面说说信息增益和熵
1. 信息论里的熵
因此先回忆一下信息论中有关信息量(就是“熵”)的定义。说有这么一个变量X,它可能的取值有n多种,分别是x1,x2,……,xn,每一种取到的概率分别是P1,P2,……,Pn,那么X的熵就定义为:

意思就是一个变量可能的变化越多(反而跟变量具体的取值没有任何关系,只和值的种类多少以及发生概率有关),它携带的信息量就越大(因此我一直觉得我们的政策法规信息量非常大,因为它变化很多,基本朝令夕改,笑)。
2. 分类系统里的熵
对分类系统来说,类别C是变量,它可能的取值是C1,C2,……,Cn,而每一个类别出现的概率是P(C1),P(C2),……,P(Cn),因此n就是类别的总数。此时分类系统的熵就可以表示为:

有同学说不好理解呀,这样想就好了,文本分类系统的作用就是输出一个表示文本属于哪个类别的值,而这个值可能是C1,C2,……,Cn,因此这个值所携带的信息量就是上式中的这么多。
3. 信息增益和熵的关系
信息增益是针对一个一个的特征而言的,就是看一个特征t,系统有它和没它的时候信息量各是多少,两者的差值就是这个特征给系统带来的信息量,即增益。系统含有特征t的时候信息量很好计算,就是刚才的式子,它表示的是包含所有特征时系统的信息量。
问题是当系统不包含t时,信息量如何计算?我们换个角度想问题,把系统要做的事情想象成这样:说教室里有很多座位,学生们每次上课进来的时 候可以随便坐,因而变化是很大的(无数种可能的座次情况);但是现在有一个座位,看黑板很清楚,听老师讲也很清楚,于是校长的小舅子的姐姐的女儿托关系 (真辗转啊),把这个座位定下来了,每次只能给她坐,别人不行,此时情况怎样?对于座次的可能情况来说,我们很容易看出以下两种情况是等价的:(1)教室
里没有这个座位;(2)教室里虽然有这个座位,但其他人不能坐(因为反正它也不能参与到变化中来,它是不变的)。
对应到我们的系统中,就是下面的等价:(1)系统不包含特征t;(2)系统虽然包含特征t,但是t已经固定了,不能变化。
我们计算分类系统不包含特征t的时候,就使用情况(2)来代替,就是计算当一个特征t不能变化时,系统的信息量是多少。这个信息量其实也有专门的名称,就叫做“条件熵”,条件嘛,自然就是指“t已经固定“这个条件。
但是问题接踵而至,例如一个特征X,它可能的取值有n多种(x1,x2,……,xn), 当计算条件熵而需要把它固定的时候,要把它固定在哪一个值上呢?答案是每一种可能都要固定一下,计算n个值,然后取均值才是条件熵。而取均值也不是简单的 加一加然后除以n,而是要用每个值出现的概率来算平均(简单理解,就是一个值出现的可能性比较大,固定在它上面时算出来的信息量占的比重就要多一些)。
因此有这样两个条件熵的表达式:

这是指特征X被固定为值xi时的条件熵,

这是指特征X被固定时的条件熵,注意与上式在意义上的区别。从刚才计算均值的讨论可以看出来,第二个式子与第一个式子的关系就是:

具体到我们文本分类系统中的特征t,t有几个可能的值呢?注意t是指一个固定的特征,比如他就是指关键词“经济”或者“体育”,当我们说特征“经济”可能的取值时,实际上只有两个,“经济”要么出现,要么不出现。一般的,t的取值只有t(代表t出现)和

(代表t不出现),注意系统包含t但t
不出现与系统根本不包含t可是两回事。
因此固定t时系统的条件熵就有了,为了区别t出现时的符号与特征t本身的符号,我们用T代表特征,而用t代表T出现,那么:

与刚才的式子对照一下,含义很清楚对吧,P(t)就是T出现的概率,

就是T不出现的概率。这个式子可以进一步展开,其中的

另一半就可以展开为:

因此特征T给系统带来的信息增益就可以写成系统原本的熵与固定特征T后的条件熵之差:

公式中的东西看上去很多,其实也都很好计算。比如P(Ci),表示类别Ci出现的概率,其实只要用1除以类别总数就得到了(这是说你平等的看待每个类别而忽略它们的大小时这样算,如果考虑了大小就要把大小的影响加进去)。再比如P(t),就是特征T出现的概率,只要用出现过T的文档数除以总文档数就可以了,再比如P(Ci|t)表示出现T的时候,类别Ci出现的概率,只要用出现了T并且属于类别Ci的文档数除以出现了T的文档数就可以了。
从以上讨论中可以看出,信息增益也是考虑了特征出现和不出现两种情况,与开方检验一样,是比较全面的,因而效果不错。但信息增益最大的问题 还在于它只能考察特征对整个系统的贡献,而不能具体到某个类别上,这就使得它只适合用来做所谓“全局”的特征选择(指所有的类都使用相同的特征集合),而 无法做“本地”的特征选择(每个类别有自己的特征集合,因为有的词,对这个类别很有区分度,对另一个类别则无足轻重)。
================
一个例子:
================
任务:
根据天气预测否去打网球
数据:
用决策树来预测:
决策树的形式类似于“如果天气怎么样,去玩;否则,怎么着怎么着”的树形分叉。那么问题是用哪个属性(即变量,如天气、温度、湿度和风力)最适合充当这颗树的根节点,在它上面没有其他节点,其他的属性都是它的后续节点。
那么借用上面所述的能够衡量一个属性区分以上数据样本的能力的“信息增益”(Information Gain)理论。
如果一个属性的信息增益量越大,这个属性作为一棵树的根节点就能使这棵树更简洁,比如说一棵树可以这么读成,如果风力弱,就去玩;风力强,再按天气、温度等分情况讨论,此时用风力作为这棵树的根节点就很有价值。如果说,风力弱,再又天气晴朗,就去玩;如果风力强,再又怎么怎么分情况讨论,这棵树相比就不够简洁了。
用熵来计算信息增益:

下面是《机器学习实战》的源码:
生成图片的:
可以看出这个算法只能处理离散值,这就是ID3致命的缺点,而且ID3的信息增益会偏向value比较多的属性,于是C.45算法出现了
它是基于ID3算法进行改进后的一种重要算法,相比于ID3算法,改进有如下几个要点:
用信息增益率来选择属性。ID3选择属性用的是子树的信息增益,这里可以用很多方法来定义信息,ID3使用的是熵(entropy, 熵是一种不纯度度量准则),也就是熵的变化值,而C4.5用的是信息增益率。
在决策树构造过程中进行剪枝,因为某些具有很少元素的结点可能会使构造的决策树过适应(Overfitting),如果不考虑这些结点可能会更好。
对非离散数据也能处理。
能够对不完整数据进行处理。
首先,说明一下如何计算信息增益率。
熟悉了ID3算法后,已经知道如何计算信息增益,计算公式如下所示(来自Wikipedia):
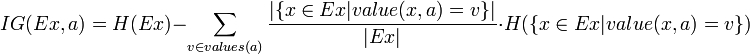
或者,用另一个更加直观容易理解的公式计算:
按照类标签对训练数据集D的属性集A进行划分,得到信息熵:
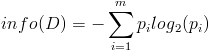
按照属性集A中每个属性进行划分,得到一组信息熵:
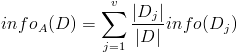
计算信息增益
然后计算信息增益,即前者对后者做差,得到属性集合A一组信息增益:
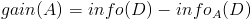
这样,信息增益就计算出来了。
计算信息增益率
下面看,计算信息增益率的公式,如下所示(来自Wikipedia):
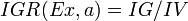
其中,IG表示信息增益,按照前面我们描述的过程来计算。而IV是我们现在需要计算的,它是一个用来考虑分裂信息的度量,分裂信息用来衡量属性分 裂数据的广度和均匀程序,计算公式如下所示(来自Wikipedia):
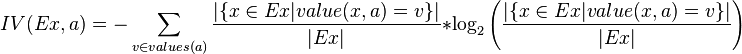
简化一下,看下面这个公式更加直观:
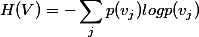
其中,V表示属性集合A中的一个属性的全部取值。
我们以一个很典型被引用过多次的训练数据集D为例,来说明C4.5算法如何计算信息增益并选择决策结点。
上面的训练集有4个属性,即属性集合A={OUTLOOK, TEMPERATURE, HUMIDITY, WINDY};而类标签有2个,即类标签集合C={Yes, No},分别表示适合户外运动和不适合户外运动,其实是一个二分类问题。
我们已经计算过信息增益,这里直接列出来,如下所示:
数据集D包含14个训练样本,其中属于类别“Yes”的有9个,属于类别“No”的有5个,则计算其信息熵:
下面对属性集中每个属性分别计算信息熵,如下所示:
根据上面的数据,我们可以计算选择第一个根结点所依赖的信息增益值,计算如下所示:
接下来,我们计算分裂信息度量H(V):
OUTLOOK属性
属性OUTLOOK有3个取值,其中Sunny有5个样本、Rainy有5个样本、Overcast有4个样本,则
TEMPERATURE属性
属性TEMPERATURE有3个取值,其中Hot有4个样本、Mild有6个样本、Cool有4个样本,则
HUMIDITY属性
属性HUMIDITY有2个取值,其中Normal有7个样本、High有7个样本,则
WINDY属性
属性WINDY有2个取值,其中True有6个样本、False有8个样本,则
根据上面计算结果,我们可以计算信息增益率,如下所示:
根据计算得到的信息增益率进行选择属性集中的属性作为决策树结点,对该结点进行分裂。
C4.5算法的优点是:产生的分类规则易于理解,准确率较高。
C4.5算法的缺点是:在构造树的过程中,需要对数据集进行多次的顺序扫描和排序,因而导致算法的低效。
C.45的算法

我自己用python实现了一下C.45
首先在UCI找数据http://archive.ics.uci.edu/ml/datasets.html
看中了这个http://archive.ics.uci.edu/ml/datasets/Thyroid+Disease
Data Set Information:
# From Garavan Institute
# Documentation: as given by Ross Quinlan
# 6 databases from the Garavan Institute in Sydney, Australia
# Approximately the following for each database:
嘿,还是C.45作者提供的数据呢,就选它了。
下了alldp.data和alldp.test
数据的文档头部需要自己添加header,把.|替换成,
剪枝和测试没写(其实我平时用java,现在学python学得不好,写得烂,没有动力写下去了,惭愧啊 (╯#-_-)╯)
好吧,说说剪枝
过拟合是决策树的大问题
决策树为什么要剪枝?原因就是避免决策树“过拟合”样本。前面的算法生成的决策树非常的详细而庞大,每个属性都被详细地加以考虑,决策树的树叶节点所覆盖的训练样本都是“纯”的。因此用这个决策树来对训练样本进行分类的话,你会发现对于训练样本而言,这个树表现堪称完美,它可以100%完美正确得对训练样本集中的样本进行分类(因为决策树本身就是100%完美拟合训练样本的产物)。但是,这会带来一个问题,如果训练样本中包含了一些错误,按照前面的算法,这些错误也会100%一点不留得被决策树学习了,这就是“过拟合”。C4.5的缔造者昆兰教授很早就发现了这个问题,他作过一个试验,在某一个数据集中,过拟合的决策树的错误率比一个经过简化了的决策树的错误率要高。那么现在的问题就来了,如何在原生的过拟合决策树的基础上,通过剪枝生成一个简化了的决策树?
第一种方法,也是最简单的方法,称之为基于误判的剪枝。这个思路很直接,完全的决策树不是过度拟合么,我再搞一个测试数据集来纠正它。对于完全决策树中的每一个非叶子节点的子树,我们尝试着把它替换成一个叶子节点,该叶子节点的类别我们用子树所覆盖训练样本中存在最多的那个类来代替,这样就产生了一个简化决策树,然后比较这两个决策树在测试数据集中的表现,如果简化决策树在测试数据集中的错误比较少,并且该子树里面没有包含另外一个具有类似特性的子树(所谓类似的特性,指的就是把子树替换成叶子节点后,其测试数据集误判率降低的特性),那么该子树就可以替换成叶子节点。该算法以bottom-up的方式遍历所有的子树,直至没有任何子树可以替换使得测试数据集的表现得以改进时,算法就可以终止。
第一种方法很直接,但是需要一个额外的测试数据集,能不能不要这个额外的数据集呢?为了解决这个问题,于是就提出了悲观剪枝。该方法剪枝的依据是训练样本集中的样本误判率。我们知道一颗分类树的每个节点都覆盖了一个样本集,根据算法这些被覆盖的样本集往往都有一定的误判率,因为如果节点覆盖的样本集的个数小于一定的阈值,那么这个节点就会变成叶子节点,所以叶子节点会有一定的误判率。而每个节点都会包含至少一个的叶子节点,所以每个节点也都会有一定的误判率。悲观剪枝就是递归得估算每个内部节点所覆盖样本节点的误判率。剪枝后该内部节点会变成一个叶子节点,该叶子节点的类别为原内部节点的最优叶子节点所决定。然后比较剪枝前后该节点的错误率来决定是否进行剪枝。该方法和前面提到的第一种方法思路是一致的,不同之处在于如何估计剪枝前分类树内部节点的错误率。
悲观剪枝的思路非常巧妙。把一颗子树(具有多个叶子节点)的分类用一个叶子节点来替代的话,误判率肯定是上升的(这是很显然的,同样的样本子集,如果用子树分类可以分成多个类,而用单颗叶子节点来分的话只能分成一个类,多个类肯定要准确一些)。于是我们需要把子树的误判计算加上一个经验性的惩罚因子。对于一颗叶子节点,它覆盖了N个样本,其中有E个错误,那么该叶子节点的错误率为(E+0.5)/N。这个0.5就是惩罚因子,那么一颗子树,它有L个叶子节点,那么该子树的误判率估计为

。这样的话,我们可以看到一颗子树虽然具有多个子节点,但由于加上了惩罚因子,所以子树的误判率计算未必占到便宜。剪枝后内部节点变成了叶子节点,其误判个数J也需要加上一个惩罚因子,变成J+0.5。那么子树是否可以被剪枝就取决于剪枝后的错误J+0.5在

的标准误差内。
对于样本的误差率e,我们可以根据经验把它估计成各种各样的分布模型,比如是二项式分布,比如是正态分布。我们以二项式分布为例,啰嗦几句来分析一下。什么是二项分布,在n次独立重复试验中,设事件A发生的次数为X,如果每次试验中中事件A发生的概率是p,那么在n次独立重复试验中,事件A恰好发生k次的概率是

其概率期望值为np,方差为np(1-p)。比如投骰子就是典型的二项分布,投骰子10次,掷得4点的次数就服从n=10,p=1/6的二项分布。
如果二项分布中n=1时,也就是只统计一次,事件A只可能有两种取值1或0,那么事件A的值所代表的分布就是伯努利分布。B(1,p)~f(1;1,p)就是伯努利分布,伯努利分布式是二项分布的一种特殊形式。比如投硬币,正面值为1,负面值为0,那么硬币为正面的概率为p=0.5,该硬币值就服从概率为0.5的伯努利分布。
当n趋于无限大时,二项式分布就正态分布,如下图。

那么一棵树错误分类一个样本值为1,正确分类一个样本值为0,该树错误分类的概率(误判率)为e(e为分布的固有属性,可以通过

统计出来),那么树的误判次数就是伯努利分布,我们可以估计出该树的误判次数均值和方差:

把子树替换成叶子节点后,该叶子的误判次数也是一个伯努利分布,其概率误判率e为(E+0.5)/N,因此叶子节点的误判次数均值为

那么,如果子树可以被叶子节点替代,它必须满足下面的条件:

这个条件就是剪枝的标准。根据置信区间,我们设定一定的显著性因子,我们可以估算出误判次数的上下界。
误判次数也可以被估计成一个正态分布,有兴趣大家可以推导一下。
用R实现一下
是c.45
读入数据,简单:
加载一个lib之后一条语句模型就出来了

R已经自动悲观剪枝了,这个模型已经非常适合了,如果非要剪枝的话:
一大堆数据还看不出什么,生成数据评价一下呗
结果还是理想的
最后,R实在是很强大-。-
参考文章:
http://www.cnblogs.com/wentingtu/archive/2012/03/24/2416235.html http://shiyanjun.cn/archives/428.html http://blog.sciencenet.cn/blog-629275-535565.html(这个也是是转的,不过我找不到原作-。-)
《机器学习实战》
把决策树研究一下,找来了一些自己觉得还可以的资料:
分类树(决策树)是一种十分常用的分类方法。他是一种监管学习,所谓监管学习说白了很简单,就是给定一堆样本,每个样本都有一组属性和一个类别,这些类别是事先确定的,那么通过学习得到一个分类器,这个分类器能够对新出现的对象给出正确的分类。这样的机器学习就被称之为监督学习。分类本质上就是一个map的过程。C4.5分类树就是决策树算法中最流行的一种。下面给出一个数据集作为算法例子的基础,比如有这么一个数据集,如下:

这个Golf数据集就是我们这篇博客讨论的基础。我们分类的目的就是根据某一天的天气状态,如天气,温度,湿度,是否刮风,来判断这一天是否适合打高尔夫球。

上面的图片已经很明显得说明了决策树的原理了
下面说说信息增益和熵
1. 信息论里的熵
因此先回忆一下信息论中有关信息量(就是“熵”)的定义。说有这么一个变量X,它可能的取值有n多种,分别是x1,x2,……,xn,每一种取到的概率分别是P1,P2,……,Pn,那么X的熵就定义为:

意思就是一个变量可能的变化越多(反而跟变量具体的取值没有任何关系,只和值的种类多少以及发生概率有关),它携带的信息量就越大(因此我一直觉得我们的政策法规信息量非常大,因为它变化很多,基本朝令夕改,笑)。
2. 分类系统里的熵
对分类系统来说,类别C是变量,它可能的取值是C1,C2,……,Cn,而每一个类别出现的概率是P(C1),P(C2),……,P(Cn),因此n就是类别的总数。此时分类系统的熵就可以表示为:

有同学说不好理解呀,这样想就好了,文本分类系统的作用就是输出一个表示文本属于哪个类别的值,而这个值可能是C1,C2,……,Cn,因此这个值所携带的信息量就是上式中的这么多。
3. 信息增益和熵的关系
信息增益是针对一个一个的特征而言的,就是看一个特征t,系统有它和没它的时候信息量各是多少,两者的差值就是这个特征给系统带来的信息量,即增益。系统含有特征t的时候信息量很好计算,就是刚才的式子,它表示的是包含所有特征时系统的信息量。
问题是当系统不包含t时,信息量如何计算?我们换个角度想问题,把系统要做的事情想象成这样:说教室里有很多座位,学生们每次上课进来的时 候可以随便坐,因而变化是很大的(无数种可能的座次情况);但是现在有一个座位,看黑板很清楚,听老师讲也很清楚,于是校长的小舅子的姐姐的女儿托关系 (真辗转啊),把这个座位定下来了,每次只能给她坐,别人不行,此时情况怎样?对于座次的可能情况来说,我们很容易看出以下两种情况是等价的:(1)教室
里没有这个座位;(2)教室里虽然有这个座位,但其他人不能坐(因为反正它也不能参与到变化中来,它是不变的)。
对应到我们的系统中,就是下面的等价:(1)系统不包含特征t;(2)系统虽然包含特征t,但是t已经固定了,不能变化。
我们计算分类系统不包含特征t的时候,就使用情况(2)来代替,就是计算当一个特征t不能变化时,系统的信息量是多少。这个信息量其实也有专门的名称,就叫做“条件熵”,条件嘛,自然就是指“t已经固定“这个条件。
但是问题接踵而至,例如一个特征X,它可能的取值有n多种(x1,x2,……,xn), 当计算条件熵而需要把它固定的时候,要把它固定在哪一个值上呢?答案是每一种可能都要固定一下,计算n个值,然后取均值才是条件熵。而取均值也不是简单的 加一加然后除以n,而是要用每个值出现的概率来算平均(简单理解,就是一个值出现的可能性比较大,固定在它上面时算出来的信息量占的比重就要多一些)。
因此有这样两个条件熵的表达式:

这是指特征X被固定为值xi时的条件熵,

这是指特征X被固定时的条件熵,注意与上式在意义上的区别。从刚才计算均值的讨论可以看出来,第二个式子与第一个式子的关系就是:

具体到我们文本分类系统中的特征t,t有几个可能的值呢?注意t是指一个固定的特征,比如他就是指关键词“经济”或者“体育”,当我们说特征“经济”可能的取值时,实际上只有两个,“经济”要么出现,要么不出现。一般的,t的取值只有t(代表t出现)和

(代表t不出现),注意系统包含t但t
不出现与系统根本不包含t可是两回事。
因此固定t时系统的条件熵就有了,为了区别t出现时的符号与特征t本身的符号,我们用T代表特征,而用t代表T出现,那么:

与刚才的式子对照一下,含义很清楚对吧,P(t)就是T出现的概率,

就是T不出现的概率。这个式子可以进一步展开,其中的

另一半就可以展开为:

因此特征T给系统带来的信息增益就可以写成系统原本的熵与固定特征T后的条件熵之差:

公式中的东西看上去很多,其实也都很好计算。比如P(Ci),表示类别Ci出现的概率,其实只要用1除以类别总数就得到了(这是说你平等的看待每个类别而忽略它们的大小时这样算,如果考虑了大小就要把大小的影响加进去)。再比如P(t),就是特征T出现的概率,只要用出现过T的文档数除以总文档数就可以了,再比如P(Ci|t)表示出现T的时候,类别Ci出现的概率,只要用出现了T并且属于类别Ci的文档数除以出现了T的文档数就可以了。
从以上讨论中可以看出,信息增益也是考虑了特征出现和不出现两种情况,与开方检验一样,是比较全面的,因而效果不错。但信息增益最大的问题 还在于它只能考察特征对整个系统的贡献,而不能具体到某个类别上,这就使得它只适合用来做所谓“全局”的特征选择(指所有的类都使用相同的特征集合),而 无法做“本地”的特征选择(每个类别有自己的特征集合,因为有的词,对这个类别很有区分度,对另一个类别则无足轻重)。
================
一个例子:
================
任务:
根据天气预测否去打网球
数据:
这个数据集来自Mitchell的机器学习,叫做是否去打网球play-tennis,以下数据仍然是从带逗号分割的文本文件,复制到纪事本,把后缀直接改为.csv就可以拿Excel打开:
*play-tennis data,其中6个变量依次为:编号、天气{Sunny、Overcast、Rain}、温度{热、冷、适中}、湿度{高、正常}、风力{强、弱}以及最后是否去玩的决策{是、否}。一个建议是把这些数据导入Excel后,另复制一份去掉变量的数据到另外一个工作簿,即只保留14个观测值。这样可以方便地使用Excel的排序功能,随时查看每个变量的取值到底有多少。*/
NO. , Outlook , Temperature , Humidity , Wind , Play
1 , Sunny , Hot , High , Weak , No
2 , Sunny , Hot , High , Strong , No
3 , Overcast , Hot , High , Weak , Yes
4 , Rain , Mild , High , Weak , Yes
5 , Rain , Cool , Normal , Weak , Yes
6 , Rain , Cool , Normal , Strong , No
7 , Overcast , Cool , Normal , Strong , Yes
8 , Sunny , Mild , High , Weak , No
9 , Sunny , Cool , Normal , Weak , Yes
10 , Rain , Mild , Normal , Weak , Yes
11 , Sunny , Mild , Normal , Strong , Yes
12 , Overcast , Mild , High , Strong , Yes
13 , Overcast , Hot , Normal , Weak , Yes
14 , Rain , Mild , High , Strong , No用决策树来预测:
决策树的形式类似于“如果天气怎么样,去玩;否则,怎么着怎么着”的树形分叉。那么问题是用哪个属性(即变量,如天气、温度、湿度和风力)最适合充当这颗树的根节点,在它上面没有其他节点,其他的属性都是它的后续节点。
那么借用上面所述的能够衡量一个属性区分以上数据样本的能力的“信息增益”(Information Gain)理论。
如果一个属性的信息增益量越大,这个属性作为一棵树的根节点就能使这棵树更简洁,比如说一棵树可以这么读成,如果风力弱,就去玩;风力强,再按天气、温度等分情况讨论,此时用风力作为这棵树的根节点就很有价值。如果说,风力弱,再又天气晴朗,就去玩;如果风力强,再又怎么怎么分情况讨论,这棵树相比就不够简洁了。
用熵来计算信息增益:
1 计算分类系统熵 类别是 是否出去玩。取值为yes的记录有9个,取值为no的有5个,即说这个样本里有9个正例,5 个负例,记为S(9+,5-),S是样本的意思(Sample)。那么P(c1) = 9/14, P(c2) = 5/14
这里熵记为Entropy(S),计算公式为:
Entropy(S)= -(9/14)*log2(9/14)-(5/14)*log2(5/14)用Matlab做数学运算
2 分别以Wind、Humidity、Outlook和Temperature作为根节点,计算其信息增益 我们来计算Wind的信息增益
当Wind固定为Weak时:记录有8条,其中正例6个,负例2个;
同样,取值为Strong的记录6个,正例负例个3个。我们可以计算相应的熵为:
Entropy(Weak)=-(6/8)*log(6/8)-(2/8)*log(2/8)=0.811 Entropy(Strong)=-(3/6)*log(3/6)-(3/6)*log(3/6)=1.0
现在就可以计算出相应的信息增益了:
所以,对于一个Wind属性固定的分类系统的信息量为 (8/14)*Entropy(Weak)+(6/14)*Entropy(Strong)
Gain(Wind)=Entropy(S)-(8/14)*Entropy(Weak)-(6/14)*Entropy(Strong)=0.940-(8/14)*0.811-(6/14)*1.0=0.048
这个公式的奥秘在于,8/14是属性Wind取值为Weak的个数占总记录的比例,同样6/14是其取值为Strong的记录个数与总记录数之比。
同理,如果以Humidity作为根节点: Entropy(High)=0.985 ; Entropy(Normal)=0.592 Gain(Humidity)=0.940-(7/14)*Entropy(High)-(7/14)*Entropy(Normal)=0.151 以Outlook作为根节点: Entropy(Sunny)=0.971 ; Entropy(Overcast)=0.0 ; Entropy(Rain)=0.971 Gain(Outlook)=0.940-(5/14)*Entropy(Sunny)-(4/14)*Entropy(Overcast)-(5/14)*Entropy(Rain)=0.247 以Temperature作为根节点: Entropy(Cool)=0.811 ; Entropy(Hot)=1.0 ; Entropy(Mild)=0.918 Gain(Temperature)=0.940-(4/14)*Entropy(Cool)-(4/14)*Entropy(Hot)-(6/14)*Entropy(Mild)=0.029 这样我们就得到了以上四个属性相应的信息增益值: Gain(Wind)=0.048 ;Gain(Humidity)=0.151 ; Gain(Outlook)=0.247 ;Gain(Temperature)=0.029 最后按照信息增益最大的原则选Outlook为根节点。子节点重复上面的步骤。这颗树可以是这样的,它读起来就跟你认为的那样:

下面是《机器学习实战》的源码:
<span style="font-size:18px;">'''
Created on Oct 12, 2010
Decision Tree Source Code for Machine Learning in Action Ch. 3
@author: Peter Harrington
'''
from math import log
import operator
def createDataSet():
dataSet = [[1, 1, 'yes'],
[1, 1, 'yes'],
[1, 0, 'no'],
[0, 1, 'no'],
[0, 1, 'no']]
labels = ['no surfacing','flippers']
#change to discrete values
return dataSet, labels
def calcShannonEnt(dataSet):
numEntries = len(dataSet)
labelCounts = {}
for featVec in dataSet: #the the number of unique elements and their occurance
currentLabel = featVec[-1]
if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key])/numEntries
shannonEnt -= prob * log(prob,2) #log base 2
return shannonEnt
def splitDataSet(dataSet, axis, value):
retDataSet = []
for featVec in dataSet:
if featVec[axis] == value:
reducedFeatVec = featVec[:axis] #chop out axis used for splitting
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSet
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1 #the last column is used for the labels
baseEntropy = calcShannonEnt(dataSet)
bestInfoGain = 0.0; bestFeature = -1
for i in range(numFeatures): #iterate over all the features
featList = [example[i] for example in dataSet]#create a list of all the examples of this feature
uniqueVals = set(featList) #get a set of unique values
newEntropy = 0.0
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet)/float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet)
infoGain = baseEntropy - newEntropy #calculate the info gain; ie reduction in entropy
if (infoGain > bestInfoGain): #compare this to the best gain so far
bestInfoGain = infoGain #if better than current best, set to best
bestFeature = i
return bestFeature #returns an integer
def majorityCnt(classList):
classCount={}
for vote in classList:
if vote not in classCount.keys(): classCount[vote] = 0
classCount[vote] += 1
sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
return sortedClassCount[0][0]
def createTree(dataSet,labels):
classList = [example[-1] for example in dataSet]
if classList.count(classList[0]) == len(classList):
return classList[0]#stop splitting when all of the classes are equal
if len(dataSet[0]) == 1: #stop splitting when there are no more features in dataSet
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet)
bestFeatLabel = labels[bestFeat]
myTree = {bestFeatLabel:{}}
del(labels[bestFeat])
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)
for value in uniqueVals:
subLabels = labels[:] #copy all of labels, so trees don't mess up existing labels
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)
return myTree
def classify(inputTree,featLabels,testVec):
firstStr = inputTree.keys()[0]
secondDict = inputTree[firstStr]
featIndex = featLabels.index(firstStr)
key = testVec[featIndex]
valueOfFeat = secondDict[key]
if isinstance(valueOfFeat, dict):
classLabel = classify(valueOfFeat, featLabels, testVec)
else: classLabel = valueOfFeat
return classLabel
def storeTree(inputTree,filename):
import pickle
fw = open(filename,'w')
pickle.dump(inputTree,fw)
fw.close()
def grabTree(filename):
import pickle
fr = open(filename)
return pickle.load(fr)
</span>生成图片的:
<span style="font-size:18px;">'''
Created on Oct 14, 2010
@author: Peter Harrington
'''
import matplotlib.pyplot as plt
decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")
def getNumLeafs(myTree):
numLeafs = 0
firstStr = myTree.keys()[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':#test to see if the nodes are dictonaires, if not they are leaf nodes
numLeafs += getNumLeafs(secondDict[key])
else: numLeafs +=1
return numLeafs
def getTreeDepth(myTree):
maxDepth = 0
firstStr = myTree.keys()[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':#test to see if the nodes are dictonaires, if not they are leaf nodes
thisDepth = 1 + getTreeDepth(secondDict[key])
else: thisDepth = 1
if thisDepth > maxDepth: maxDepth = thisDepth
return maxDepth
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
xytext=centerPt, textcoords='axes fraction',
va="center", ha="center", bbox=nodeType, arrowprops=arrow_args )
def plotMidText(cntrPt, parentPt, txtString):
xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)
def plotTree(myTree, parentPt, nodeTxt):#if the first key tells you what feat was split on
numLeafs = getNumLeafs(myTree) #this determines the x width of this tree
depth = getTreeDepth(myTree)
firstStr = myTree.keys()[0] #the text label for this node should be this
cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
plotMidText(cntrPt, parentPt, nodeTxt)
plotNode(firstStr, cntrPt, parentPt, decisionNode)
secondDict = myTree[firstStr]
plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':#test to see if the nodes are dictonaires, if not they are leaf nodes
plotTree(secondDict[key],cntrPt,str(key)) #recursion
else: #it's a leaf node print the leaf node
plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD
#if you do get a dictonary you know it's a tree, and the first element will be another dict
def createPlot(inTree):
fig = plt.figure(1, facecolor='white')
fig.clf()
axprops = dict(xticks=[], yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) #no ticks
#createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
plotTree.totalW = float(getNumLeafs(inTree))
plotTree.totalD = float(getTreeDepth(inTree))
plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0;
plotTree(inTree, (0.5,1.0), '')
plt.show()
#def createPlot():
# fig = plt.figure(1, facecolor='white')
# fig.clf()
# createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
# plotNode('a decision node', (0.5, 0.1), (0.1, 0.5), decisionNode)
# plotNode('a leaf node', (0.8, 0.1), (0.3, 0.8), leafNode)
# plt.show()
def retrieveTree(i):
listOfTrees =[{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}},
{'no surfacing': {0: 'no', 1: {'flippers': {0: {'head': {0: 'no', 1: 'yes'}}, 1: 'no'}}}}
]
return listOfTrees[i]
#createPlot(thisTree)</span>可以看出这个算法只能处理离散值,这就是ID3致命的缺点,而且ID3的信息增益会偏向value比较多的属性,于是C.45算法出现了
它是基于ID3算法进行改进后的一种重要算法,相比于ID3算法,改进有如下几个要点:
用信息增益率来选择属性。ID3选择属性用的是子树的信息增益,这里可以用很多方法来定义信息,ID3使用的是熵(entropy, 熵是一种不纯度度量准则),也就是熵的变化值,而C4.5用的是信息增益率。
在决策树构造过程中进行剪枝,因为某些具有很少元素的结点可能会使构造的决策树过适应(Overfitting),如果不考虑这些结点可能会更好。
对非离散数据也能处理。
能够对不完整数据进行处理。
首先,说明一下如何计算信息增益率。
熟悉了ID3算法后,已经知道如何计算信息增益,计算公式如下所示(来自Wikipedia):
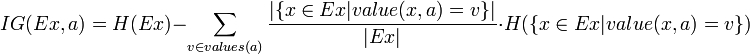
或者,用另一个更加直观容易理解的公式计算:
按照类标签对训练数据集D的属性集A进行划分,得到信息熵:
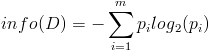
按照属性集A中每个属性进行划分,得到一组信息熵:
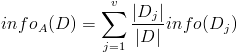
计算信息增益
然后计算信息增益,即前者对后者做差,得到属性集合A一组信息增益:
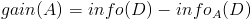
这样,信息增益就计算出来了。
计算信息增益率
下面看,计算信息增益率的公式,如下所示(来自Wikipedia):
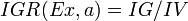
其中,IG表示信息增益,按照前面我们描述的过程来计算。而IV是我们现在需要计算的,它是一个用来考虑分裂信息的度量,分裂信息用来衡量属性分 裂数据的广度和均匀程序,计算公式如下所示(来自Wikipedia):
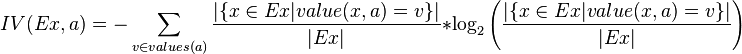
简化一下,看下面这个公式更加直观:
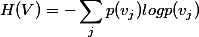
其中,V表示属性集合A中的一个属性的全部取值。
我们以一个很典型被引用过多次的训练数据集D为例,来说明C4.5算法如何计算信息增益并选择决策结点。
上面的训练集有4个属性,即属性集合A={OUTLOOK, TEMPERATURE, HUMIDITY, WINDY};而类标签有2个,即类标签集合C={Yes, No},分别表示适合户外运动和不适合户外运动,其实是一个二分类问题。
我们已经计算过信息增益,这里直接列出来,如下所示:
数据集D包含14个训练样本,其中属于类别“Yes”的有9个,属于类别“No”的有5个,则计算其信息熵:
| 1 | Info(D) = -9/14 * log2(9/14) - 5/14 * log2(5/14) = 0.940 |
| 1 | Info(OUTLOOK) = 5/14 * [- 2/5 * log2(2/5) – 3/5 * log2(3/5)] + 4/14 * [ - 4/4 * log2(4/4) - 0/4 * log2(0/4)] + 5/14 * [ - 3/5 * log2(3/5) – 2/5 * log2(2/5)] = 0.694 |
| 2 | Info(TEMPERATURE) = 4/14 * [- 2/4 * log2(2/4) – 2/4 * log2(2/4)] + 6/14 * [ - 4/6 * log2(4/6) - 2/6 * log2(2/6)] + 4/14 * [ - 3/4 * log2(3/4) – 1/4 * log2(1/4)] = 0.911 |
| 3 | Info(HUMIDITY) = 7/14 * [- 3/7 * log2(3/7) – 4/7 * log2(4/7)] + 7/14 * [ - 6/7 * log2(6/7) - 1/7 * log2(1/7)] = 0.789 |
| 4 | Info(WINDY) = 6/14 * [- 3/6 * log2(3/6) – 3/6 * log2(3/6)] + 8/14 * [ - 6/8 * log2(6/8) - 2/8 * log2(2/8)] = 0.892 |
| 1 | Gain(OUTLOOK) = Info(D) - Info(OUTLOOK) = 0.940 - 0.694 = 0.246 |
| 2 | Gain(TEMPERATURE) = Info(D) - Info(TEMPERATURE) = 0.940 - 0.911 = 0.029 |
| 3 | Gain(HUMIDITY) = Info(D) - Info(HUMIDITY) = 0.940 - 0.789 = 0.151 |
| 4 | Gain(WINDY) = Info(D) - Info(WINDY) = 0.940 - 0.892 = 0.048 |
OUTLOOK属性
属性OUTLOOK有3个取值,其中Sunny有5个样本、Rainy有5个样本、Overcast有4个样本,则
| 1 | H(OUTLOOK) = - 5/14 * log2(5/14) - 5/14 * log2(5/14) - 4/14 * log2(4/14) = 1.577406282852345 |
属性TEMPERATURE有3个取值,其中Hot有4个样本、Mild有6个样本、Cool有4个样本,则
| 1 | H(TEMPERATURE) = - 4/14 * log2(4/14) - 6/14 * log2(6/14) - 4/14 * log2(4/14) = 1.5566567074628228 |
属性HUMIDITY有2个取值,其中Normal有7个样本、High有7个样本,则
| 1 | H(HUMIDITY) = - 7/14 * log2(7/14) - 7/14 * log2(7/14) = 1.0 |
属性WINDY有2个取值,其中True有6个样本、False有8个样本,则
| 1 | H(WINDY) = - 6/14 * log2(6/14) - 8/14 * log2(8/14) = 0.9852281360342516 |
| 1 | IGR(OUTLOOK) = Info(OUTLOOK) / H(OUTLOOK) = 0.246/1.577406282852345 = 0.15595221261270145 |
| 2 | IGR(TEMPERATURE) = Info(TEMPERATURE) / H(TEMPERATURE) = 0.029 / 1.5566567074628228 = 0.018629669509642094 |
| 3 | IGR(HUMIDITY) = Info(HUMIDITY) / H(HUMIDITY) = 0.151/1.0 = 0.151 |
| 4 | IGR(WINDY) = Info(WINDY) / H(WINDY) = 0.048/0.9852281360342516 = 0.048719680492692784 |
C4.5算法的优点是:产生的分类规则易于理解,准确率较高。
C4.5算法的缺点是:在构造树的过程中,需要对数据集进行多次的顺序扫描和排序,因而导致算法的低效。
C.45的算法

我自己用python实现了一下C.45
首先在UCI找数据http://archive.ics.uci.edu/ml/datasets.html
看中了这个http://archive.ics.uci.edu/ml/datasets/Thyroid+Disease
Data Set Information:
# From Garavan Institute
# Documentation: as given by Ross Quinlan
# 6 databases from the Garavan Institute in Sydney, Australia
# Approximately the following for each database:
嘿,还是C.45作者提供的数据呢,就选它了。
下了alldp.data和alldp.test
数据的文档头部需要自己添加header,把.|替换成,
<span style="font-size:18px;">__author__ = 'tyan'
#coding=utf-8
import os
import math
import copy
import operator
from collections import Counter
class Node:
def __init__(self, val, child=[], condition=None):
self.val = val
self.child = child
self.condition = condition
class C4_5(object):
#初始化
def __init__(self, trainSet, format, rule):
self.tree = Node(None, [])
trainSet = list(trainSet)
self.attributes = trainSet[0][:-1]
self.format = format
self.trainSet = trainSet[1:]
self.dataLen = len(self.trainSet)
self.rule = rule
def startTrain(self):
self.train(self.trainSet, self.tree, self.attributes, 0)
#处理缺失值,我这是图方便,实际测试predict时,不建议用测试样本中的数据来生成缺失数据,应该用训练数据来生成
def rep_miss(self, dataSet):
exp = copy.deepcopy(dataSet)
for attr in self.attributes:
idx = self.attributes.index(attr)
if self.format[idx] == 'nominal':
#expN 用频率最大的填补缺失
expN = getDefault([item[idx] for item in exp])
for item in exp:
if item[idx] == '?':
item[idx] = expN
else:
num_lst = [float(item[idx]) for item in exp if item[idx] != '?']
mean = sum(num_lst) / len(num_lst)
for item in exp:
if item[idx] == '?':
item[idx] = mean
return exp
#寻找合适的分割点
def split(self, lst, idx):
split_candidate = []
for x, y in zip (lst, lst[1:]):
if (x[-1] != y[-1]) and (x[idx] != y[idx]):
split_candidate.append( (x[idx] + y[idx]) / 2 )
return split_candidate
def preProcess(self, validFile):
validSet = list( readData(validFile) )
validData = validSet[1:]
exp = self.rep_miss(validData)
return exp
def rule_generator(self, tree, single_rule):
#if flag:
# self.rule = []
#print tree
if tree.child:
if isinstance(tree.val, list):
single_rule.append(tree.val)
if tree.child[0] == 'negative':
single_rule.append(['class', '=', 'negative'])
self.rule.append(single_rule)
elif tree.child[0] == 'increased binding proteinval':
single_rule.append(['class', '=', 'increased binding proteinval'])
self.rule.append(single_rule)
elif tree.child[0] == 'decreased binding protein':
single_rule.append(['class', '=', 'decreased binding protein'])
self.rule.append(single_rule)
else:
for item in tree.child:
self.rule_generator(item, list(single_rule))
def train(self, dataSet, tree, attributes, default):
if len(dataSet) == 0:
return Node(default)
elif allequal([item[-1] for item in dataSet]):
return Node(dataSet[0][-1])
elif len(attributes) == 0:
return Node(getDefault([item[-1] for item in dataSet]))
else:
#选取最大信息增益
best = self.choose_attr(attributes, dataSet)
if best == 0:
return Node(getDefault([item[-1] for item in dataSet]))
print best
tree.val = best[0]
#离散值的情况
idx = self.attributes.index(best[0])
if best[1] == 'nom':
attributes.remove(best[0])
for v in unique(item[idx] for item in dataSet):
subDataSet = [item for item in dataSet if item[idx] == v]
#选取条件熵后的子数据集递归构造树
subTree = self.train(subDataSet, Node(None, []), list(attributes), getDefault(item[-1] for item in dataSet))
branch = Node([best[0], '==', v], [subTree])
tree.child.append(branch)
else:#连续型变量
subDataSet1 = [item for item in dataSet if float(item[idx]) > best[2]]
default = getDefault(item[-1] for item in dataSet)
if len(subDataSet1) == len(dataSet):
print '!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!'
return default
subTree1 = self.train(subDataSet1, Node(None), list(attributes), default)
subTree1.condition = [best[0], '>', str(best[2])]
tree.child.append(subTree1)
subDataSet2 = [item for item in dataSet if float(item[idx]) <= best[2]]
subTree2 = self.train(subDataSet2, Node(None), list(attributes), default)
subTree2.condition=[best[0], '<=', str(best[2])]
tree.child.append(subTree2)
return tree
#求最大信息增益比
def choose_attr(self, attributes, dataSet):
maxIGR = 0.0
dataLen = float(len(dataSet))
group = [item[-1] for item in dataSet]
groupC = Counter(group).items()
#sysGI 分类系统熵
sysGI = entropy([vl/dataLen for k,vl in groupC])
for attr in attributes:
idx = self.attributes.index(attr)
gain = sysGI
h = 0.0 #信息裂度
if self.format[idx] == 'nominal':
#expN 把频率最大的填补缺失
expN = getDefault([item[idx] for item in dataSet])
for item in dataSet:
if item[idx] == '?':
item[idx] = expN
for i in unique([item[idx] for item in dataSet]):
#expG:该attr的所有分类结果
expG = [item[-1] for item in dataSet if item[idx] == i]
expGC = Counter(expG).items()
split_len = float(len(expG))
gain -= split_len/dataLen * entropy([vl/split_len for k,vl in expGC])
#计算信息裂度
groupValueC = Counter([item[idx] for item in dataSet ]).items()
h -= entropy([vl/len(dataSet) for k,vl in groupValueC])
if h == 0:
continue #不知道为什么会有0,郁闷
igr = gain / h
if igr > maxIGR:
maxIGR = gain
best = [attr, 'nom']
else:
num_lst = [float(item[idx]) for item in dataSet if item[idx] != '?']
if len(num_lst) == 0:
print "Error!!!!"
mean = sum(num_lst) / len(num_lst)
exps = list(dataSet)
for item in exps:
if item[idx] == '?':
item[idx] = mean
else:
item[idx] = float(item[idx])
exps.sort(key = operator.itemgetter(idx))
split_candidate = self.split(exps, idx)
for thresh in split_candidate:
gain = sysGI
#expG:该attr的所有分类结果
expG1 = [item[-1] for item in exps if float(item[idx]) > thresh]
expG2 = [item[-1] for item in exps if float(item[idx]) <= thresh]
len1 = float(len(expG1))
len2 = float(len(expG2))
if len1 == 0 or len2 == 0:
gain = 0
else:
expGC1 = Counter(expG1).items()
expGC2 = Counter(expG2).items()
gain -= len1/dataLen * entropy([vl/len1 for k,vl in expGC1])
gain -= len1/dataLen * entropy([vl/len1 for k,vl in expGC1])
h -= entropy([len1/len(dataSet), len2/len(dataSet)])
igr = gain / h
if igr > maxIGR:
maxIGR = igr
best = [attr, 'num', thresh]
#print max_gain
if maxIGR <= 0:
return 0
return best
def entropy(lst):
entrop = 0.0
for p in lst:
if p == 0:
continue
entrop -= p * math.log(p, 2)
return entrop
def unique(seq):
keys = {}
for e in seq:
keys[e] = 1
return keys.keys()
def allequal(seq):
flag = seq[0]
for item in seq:
if item != flag:
return 0
return 1
def readData(inputfile):
data = []
abspath = os.path.abspath(inputfile)
with open(abspath,"r")as file:
text = file.readlines()
for line in text:
items = line.split(',')[:-1]
items.pop(26)
items.pop(26)
data.append(items)
print data[0]
print len(data[0])
return data
#这个函数是选取频率最大的
def getDefault(lst):
frequent = Counter(lst)
mostfrequent = frequent.most_common(2)
if mostfrequent[0][0] == '?':
mostfrequent = mostfrequent[1:]
return mostfrequent[0][0]
format = []
for i in range(28):
format.append("nominal")
for i in [0,17,19,21,23,25]:
format[i] = "numeric"
inputfile = "allbp"
trainSet = readData(inputfile)
classifier = C4_5(trainSet, format, [])
classifier.startTrain()
</span>跑了一下,明显过拟合了("▔□▔)/\("▔□▔)/剪枝和测试没写(其实我平时用java,现在学python学得不好,写得烂,没有动力写下去了,惭愧啊 (╯#-_-)╯)
好吧,说说剪枝
过拟合是决策树的大问题
决策树为什么要剪枝?原因就是避免决策树“过拟合”样本。前面的算法生成的决策树非常的详细而庞大,每个属性都被详细地加以考虑,决策树的树叶节点所覆盖的训练样本都是“纯”的。因此用这个决策树来对训练样本进行分类的话,你会发现对于训练样本而言,这个树表现堪称完美,它可以100%完美正确得对训练样本集中的样本进行分类(因为决策树本身就是100%完美拟合训练样本的产物)。但是,这会带来一个问题,如果训练样本中包含了一些错误,按照前面的算法,这些错误也会100%一点不留得被决策树学习了,这就是“过拟合”。C4.5的缔造者昆兰教授很早就发现了这个问题,他作过一个试验,在某一个数据集中,过拟合的决策树的错误率比一个经过简化了的决策树的错误率要高。那么现在的问题就来了,如何在原生的过拟合决策树的基础上,通过剪枝生成一个简化了的决策树?
第一种方法,也是最简单的方法,称之为基于误判的剪枝。这个思路很直接,完全的决策树不是过度拟合么,我再搞一个测试数据集来纠正它。对于完全决策树中的每一个非叶子节点的子树,我们尝试着把它替换成一个叶子节点,该叶子节点的类别我们用子树所覆盖训练样本中存在最多的那个类来代替,这样就产生了一个简化决策树,然后比较这两个决策树在测试数据集中的表现,如果简化决策树在测试数据集中的错误比较少,并且该子树里面没有包含另外一个具有类似特性的子树(所谓类似的特性,指的就是把子树替换成叶子节点后,其测试数据集误判率降低的特性),那么该子树就可以替换成叶子节点。该算法以bottom-up的方式遍历所有的子树,直至没有任何子树可以替换使得测试数据集的表现得以改进时,算法就可以终止。
第一种方法很直接,但是需要一个额外的测试数据集,能不能不要这个额外的数据集呢?为了解决这个问题,于是就提出了悲观剪枝。该方法剪枝的依据是训练样本集中的样本误判率。我们知道一颗分类树的每个节点都覆盖了一个样本集,根据算法这些被覆盖的样本集往往都有一定的误判率,因为如果节点覆盖的样本集的个数小于一定的阈值,那么这个节点就会变成叶子节点,所以叶子节点会有一定的误判率。而每个节点都会包含至少一个的叶子节点,所以每个节点也都会有一定的误判率。悲观剪枝就是递归得估算每个内部节点所覆盖样本节点的误判率。剪枝后该内部节点会变成一个叶子节点,该叶子节点的类别为原内部节点的最优叶子节点所决定。然后比较剪枝前后该节点的错误率来决定是否进行剪枝。该方法和前面提到的第一种方法思路是一致的,不同之处在于如何估计剪枝前分类树内部节点的错误率。
悲观剪枝的思路非常巧妙。把一颗子树(具有多个叶子节点)的分类用一个叶子节点来替代的话,误判率肯定是上升的(这是很显然的,同样的样本子集,如果用子树分类可以分成多个类,而用单颗叶子节点来分的话只能分成一个类,多个类肯定要准确一些)。于是我们需要把子树的误判计算加上一个经验性的惩罚因子。对于一颗叶子节点,它覆盖了N个样本,其中有E个错误,那么该叶子节点的错误率为(E+0.5)/N。这个0.5就是惩罚因子,那么一颗子树,它有L个叶子节点,那么该子树的误判率估计为

。这样的话,我们可以看到一颗子树虽然具有多个子节点,但由于加上了惩罚因子,所以子树的误判率计算未必占到便宜。剪枝后内部节点变成了叶子节点,其误判个数J也需要加上一个惩罚因子,变成J+0.5。那么子树是否可以被剪枝就取决于剪枝后的错误J+0.5在

的标准误差内。
对于样本的误差率e,我们可以根据经验把它估计成各种各样的分布模型,比如是二项式分布,比如是正态分布。我们以二项式分布为例,啰嗦几句来分析一下。什么是二项分布,在n次独立重复试验中,设事件A发生的次数为X,如果每次试验中中事件A发生的概率是p,那么在n次独立重复试验中,事件A恰好发生k次的概率是

其概率期望值为np,方差为np(1-p)。比如投骰子就是典型的二项分布,投骰子10次,掷得4点的次数就服从n=10,p=1/6的二项分布。
如果二项分布中n=1时,也就是只统计一次,事件A只可能有两种取值1或0,那么事件A的值所代表的分布就是伯努利分布。B(1,p)~f(1;1,p)就是伯努利分布,伯努利分布式是二项分布的一种特殊形式。比如投硬币,正面值为1,负面值为0,那么硬币为正面的概率为p=0.5,该硬币值就服从概率为0.5的伯努利分布。
当n趋于无限大时,二项式分布就正态分布,如下图。

那么一棵树错误分类一个样本值为1,正确分类一个样本值为0,该树错误分类的概率(误判率)为e(e为分布的固有属性,可以通过

统计出来),那么树的误判次数就是伯努利分布,我们可以估计出该树的误判次数均值和方差:

把子树替换成叶子节点后,该叶子的误判次数也是一个伯努利分布,其概率误判率e为(E+0.5)/N,因此叶子节点的误判次数均值为

那么,如果子树可以被叶子节点替代,它必须满足下面的条件:

这个条件就是剪枝的标准。根据置信区间,我们设定一定的显著性因子,我们可以估算出误判次数的上下界。
误判次数也可以被估计成一个正态分布,有兴趣大家可以推导一下。
用R实现一下
是c.45
读入数据,简单:
thyData = read.table("/home/tyan/DataSet/thyroid-disease/allbp",sep=',',header=T,na.strings='?')
testData = read.table("/home/tyan/DataSet/thyroid-disease/allbp.test",sep=',',header=T,na.strings='?')如果读了之后加header的话:举个例子names(x) <- c('v1', 'v2')加载一个lib之后一条语句模型就出来了
library(rpart) rt<-rpart(thyData$classes~.,data=thyData[,1:26]) rt简单得吓人:
n= 2800
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 2800 133 negative (0.003214286 0.044285714 0.952500000)
2) T4U>=1.275 172 82 increased binding protein (0.000000000 0.523255814 0.476744186)
4) T3>=2.85 81 13 increased binding protein (0.000000000 0.839506173 0.160493827) *
5) T3< 2.85 91 22 negative (0.000000000 0.241758242 0.758241758)
10) T3.measured=f 24 11 increased binding protein (0.000000000 0.541666667 0.458333333)
20) TT4< 141.5 14 3 increased binding protein (0.000000000 0.785714286 0.214285714) *
21) TT4>=141.5 10 2 negative (0.000000000 0.200000000 0.800000000) *
11) T3.measured=t 67 9 negative (0.000000000 0.134328358 0.865671642)
22) TT4>=179.5 7 2 increased binding protein (0.000000000 0.714285714 0.285714286) *
23) TT4< 179.5 60 4 negative (0.000000000 0.066666667 0.933333333) *
3) T4U< 1.275 2628 43 negative (0.003424658 0.012937595 0.983637747)
6) T3>=2.85 150 28 negative (0.000000000 0.186666667 0.813333333)
12) TSH>=2.95 15 5 increased binding protein (0.000000000 0.666666667 0.333333333) *
13) TSH< 2.95 135 18 negative (0.000000000 0.133333333 0.866666667)
26) T4U>=1.135 30 11 negative (0.000000000 0.366666667 0.633333333)
52) TSH< 1.25 22 11 increased binding protein (0.000000000 0.500000000 0.500000000)
104) TT4>=143.5 10 3 increased binding protein (0.000000000 0.700000000 0.300000000) *
105) TT4< 143.5 12 4 negative (0.000000000 0.333333333 0.666666667) *
53) TSH>=1.25 8 0 negative (0.000000000 0.000000000 1.000000000) *
27) T4U< 1.135 105 7 negative (0.000000000 0.066666667 0.933333333) *
7) T3< 2.85 2478 15 negative (0.003631961 0.002421308 0.993946731)
14) T4U< 0.595 24 8 negative (0.333333333 0.000000000 0.666666667)
28) TT4< 60 9 2 decreased binding protein (0.777777778 0.000000000 0.222222222) *
29) TT4>=60 15 1 negative (0.066666667 0.000000000 0.933333333) *
15) T4U>=0.595 2454 7 negative (0.000407498 0.002444988 0.997147514)
30) TT4>=159.5 92 6 negative (0.000000000 0.065217391 0.934782609)
60) FTI< 141 8 2 increased binding protein (0.000000000 0.750000000 0.250000000) *
61) FTI>=141 84 0 negative (0.000000000 0.000000000 1.000000000) *
31) TT4< 159.5 2362 1 negative (0.000423370 0.000000000 0.999576630) *生成图片plot(rt) text(rt)

R已经自动悲观剪枝了,这个模型已经非常适合了,如果非要剪枝的话:
printcp(rt) rt2<-prune(rt,cp=0.08)预测一下:
predict(rt,testData)
一大堆数据还看不出什么,生成数据评价一下呗
(rt <- mean(abs(rt.predictions-as.numeric(testData[,'classes'])))) #MAE 绝对平均误差 (rt <- mean((rt.predictions-as.numeric(testData[,'classes']))^2)) #MSE 均方误差 (rt <- mean((rt.predictions-as.numeric(testData[,'classes']))^2)/ mean((mean(as.numeric(testData[,'classes']))-as.numeric(testData[,'classes']))^2))
#NMAE标准化后的绝对平均误差 : 计算模型预测性能和基准模型的预测性能之间的比率
(rt <- mean(abs(rt.predictions-as.numeric(testData[,'classes'])))) [1] 2.630621 > > > (rt <- mean((rt.predictions-as.numeric(testData[,'classes']))^2)) [1] 7.178987 > > > (rt <- mean((rt.predictions-as.numeric(testData[,'classes']))^2)/ + mean((mean(as.numeric(testData[,'classes']))-as.numeric(testData[,'classes']))^2)) [1] 159.3747
结果还是理想的
最后,R实在是很强大-。-
参考文章:
http://www.cnblogs.com/wentingtu/archive/2012/03/24/2416235.html http://shiyanjun.cn/archives/428.html http://blog.sciencenet.cn/blog-629275-535565.html(这个也是是转的,不过我找不到原作-。-)
《机器学习实战》
相关文章推荐
- 机器学习(周志华)习题解答4.3: Python小白详解ID3决策树的实现
- [置顶] 《统计学习方法》 决策树 ID3和C4.5 生成算法 Python实现
- Python实现决策树(ID3、C4.5)
- 决策树(ID3,C4.5)Python实现
- 机器学习经典算法详解及Python实现–决策树(Decision Tree)
- 决策树ID3和C4.5算法Python实现源码
- 分类算法-----决策树(ID3)算法原理和Python实现
- CART分类决策树、回归树和模型树算法详解及Python实现
- 一步一步详解ID3和C4.5的C++实现
- 决策树ID3的Python实现
- 机器学习经典算法详解及Python实现--决策树(Decision Tree)
- 机器学习经典算法详解及Python实现--决策树(Decision Tree)
- 一步一步详解ID3和C4.5的C++实现
- 一步一步详解ID3和C4.5的C++实现
- ID3决策树的算法原理与python实现
- 机器学习经典算法详解及Python实现–决策树
- 机器学习经典算法详解及Python实现--CART分类决策树、回归树和模型树
- 机器学习经典算法详解及Python实现--决策树(Decision Tree)
- 决策树ID3和C4.5算法Python实现源码
- 机器学习经典算法详解及Python实现--CART分类决策树、回归树和模型树
