算法学习_分治法
2014-11-01 17:35
127 查看
一、分治法包含三个步骤:
(1)分解:在分解阶段,将数据分解为更小,更容易管理的部分
(2)求解:对每个分解出的部分进行处理(递归)
(3)合并:将每部分处理的结果进行合并
二、常用实例:
(1)归并排序
(2)二分查找
(3)幂次方
(4)斐波那契数列
(5).......
下面为代码实现:
而斐波那契数列的算法分析,通过幂次方的方法使得算法复杂度从指数级转向对数级。下面为转载一篇斐波那契数列的算法分析:
http://www.cnblogs.com/CCBB/archive/2011/09/14/1443441.html,该作者分析的非常详细和全面。
斐波那契数列算法分析
背景:
假定你有一雄一雌一对刚出生的兔子,它们在长到一个月大小时开始交配,在第二月结束时,雌兔子产下另一对兔子,过了一个月后它们也开始繁殖,如此这般持续下去。每只雌兔在开始繁殖时每月都产下一对兔子,假定没有兔子死亡,在一年后总共会有多少对兔子?
在一月底,最初的一对兔子交配,但是还只有1对兔子;在二月底,雌兔产下一对兔子,共有2对兔子;在三月底,最老的雌兔产下第二对兔子,共有3对兔子;在四月底,最老的雌兔产下第三对兔子,两个月前生的雌兔产下一对兔子,共有5对兔子;……如此这般计算下去,兔子对数分别是:1,
1, 2, 3, 5, 8, 13, 21, 34, 55,89, 144, ...看出规律了吗?从第3个数目开始,每个数目都是前面两个数目之和。这就是著名的斐波那契(Fibonacci)数列。
有趣问题:
1,有一段楼梯有10级台阶,规定每一步只能跨一级或两级,要登上第10级台阶有几种不同的走法?
答:这就是一个斐波那契数列:登上第一级台阶有一种登法;登上两级台阶,有两种登法;登上三级台阶,有三种登法;登上四级台阶,有五种方法……所以,1,2,3,5,8,13……登上十级,有89种。
2,数列中相邻两项的前项比后项的极限是多少,就是问,当n趋于无穷大时,F(n)/F(n+1)的极限是多少?
答:这个可由它的通项公式直接得到,极限是(-1+√5)/2,这个就是所谓的黄金分割点,也是代表大自然的和谐的一个数字。
数学表示:
Fibonacci数列的数学表达式就是:
F(n) = F(n-1) + F(n-2)
F(1) = 1
F(2) = 1
递归程序1:
Fibonacci数列可以用很直观的二叉递归程序来写,用C++语言的描述如下:
long fib1(int n)
{
if (n <= 2)
{
return 1;
}
else
{
return fib1(n-1) + fib1(n-2);
}
}
看上去程序的递归使用很恰当,可是在用VC2005的环境下测试n=37的时候用了大约3s,而n=45的时候基本下楼打完饭也看不到结果……显然这种递归的效率太低了!!
递归效率分析:
例如,用下面一个测试函数:
long fib1(int n, int* arr)
{
arr
++;
if (n <= 2)
{
return 1;
}
else
{
return fib1(n-1, arr) + fib1(n-2, arr);
}
}
这时,可以得到每个fib(i)被计算的次数:
fib(10) = 1 fib(9) = 1 fib(8) = 2 fib(7) = 3
fib(6) = 5 fib(5) = 8 fib(4) = 13 fib(3) = 21
fib(2) = 34 fib(1) = 55 fib(0) = 34
可见,计算次数呈反向的Fibonacci数列,这显然造成了大量重复计算。
我们令T(N)为函数fib(n)的运行时间,当N>=2的时候我们分析可知:
T(N) = T(N-1) + T(N-2) + 2
而fib(n) = fib(n-1) + fib(n-2),所以有T(N) >= fib(n),归纳法证明可得:
fib(N) < (5/3)^N
当N>4时,fib(N)>=
(3/2)^N
标准写法:
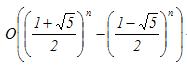
显然这个O((3/2)^N) 是以指数增长的算法,基本上是最坏的情况。
其实,这违反了递归的一个规则:合成效益法则。
合成效益法则(Compound interest rule):在求解一个问题的同一实例的时候,切勿在不同的递归调用中做重复性的工作。
所以在上面的代码中调用fib(N-1)的时候实际上同时计算了fib(N-2)。这种小的重复计算在递归过程中就会产生巨大的运行时间。
递归程序2:
用一叉递归程序就可以得到近似线性的效率,用C++语言的描述如下:
long fib(int n, long a, long b, int count)
{
if (count == n)
return b;
return fib(n, b, a+b, ++count);
}
long fib2(int n)
{
return fib(n, 0, 1, 1);
}
这种方法虽然是递归了,但是并不直观,而且效率上相比下面的迭代循环并没有优势。
迭代解法:
Fibonacci数列用迭代程序来写也很容易,用C++语言的描述如下:
//也可以用数组将每次计算的f(n)存储下来,用来下次计算用(空间换时间)
long fib3 (int n)
{
long x = 0, y = 1;
for (int j = 1; j < n; j++)
{
y = x + y;
x = y - x;
}
return y;
}
这时程序的效率显然为O(N),N
= 45的时候<1s就能得到结果。
矩阵乘法:
我们将数列写成:
Fibonacci[0] = 0,Fibonacci[1] = 1
Fibonacci
= Fibonacci[n-1] + Fibonacci[n-2] (n >= 2)
可以将它写成矩阵乘法形式:
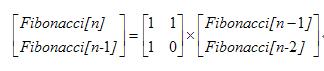
将右边连续的展开就得到:
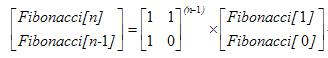
下面就是要用O(log(n))的算法计算:

显然用二分法来求,结合一些面向对象的概念,C++代码如下:
class Matrix
{
public:
long matr[2][2];
Matrix(const Matrix&rhs);
Matrix(long a, long b, long c, long d);
Matrix& operator=(const Matrix&);
friend Matrix operator*(const Matrix& lhs, const Matrix& rhs)
{
Matrix ret(0,0,0,0);
ret.matr[0][0] = lhs.matr[0][0]*rhs.matr[0][0] + lhs.matr[0][1]*rhs.matr[1][0];
ret.matr[0][1] = lhs.matr[0][0]*rhs.matr[0][1] + lhs.matr[0][1]*rhs.matr[1][1];
ret.matr[1][0] = lhs.matr[1][0]*rhs.matr[0][0] + lhs.matr[1][1]*rhs.matr[1][0];
ret.matr[1][1] = lhs.matr[1][0]*rhs.matr[0][1] + lhs.matr[1][1]*rhs.matr[1][1];
return ret;
}
};
Matrix::Matrix(long a, long b, long c, long d)
{
this->matr[0][0] = a;
this->matr[0][1] = b;
this->matr[1][0] = c;
this->matr[1][1] = d;
}
Matrix::Matrix(const Matrix &rhs)
{
this->matr[0][0] = rhs.matr[0][0];
this->matr[0][1] = rhs.matr[0][1];
this->matr[1][0] = rhs.matr[1][0];
this->matr[1][1] = rhs.matr[1][1];
}
Matrix& Matrix::operator =(const Matrix &rhs)
{
this->matr[0][0] = rhs.matr[0][0];
this->matr[0][1] = rhs.matr[0][1];
this->matr[1][0] = rhs.matr[1][0];
this->matr[1][1] = rhs.matr[1][1];
return *this;
}
Matrix power(const Matrix& m, int n)
{
if (n == 1)
return m;
if (n%2 == 0)
return power(m*m, n/2);
else
return power(m*m, n/2) * m;
}
long fib4 (int n)
{
Matrix matrix0(1, 1, 1, 0);
matrix0 = power(matrix0, n-1);
return matrix0.matr[0][0];
}
这时程序的效率为O(log(N)) 。
公式解法:
在O(1)的时间就能求得到F(n)了:
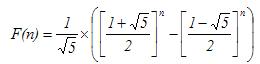
注意:其中[x]表示取距离x最近的整数。
用C++写的代码如下:
long fib5(int n)
{
double z = sqrt(5.0);
double x = (1 + z)/2;
double y = (1 - z)/2;
return (pow(x, n) - pow(y, n))/z + 0.5;
}
这个与数学库实现开方和乘方本身效率有关的,我想应该还是在O(log(n))的效率。
总结:
上面给出了5中求解斐波那契数列的方法,用测试程序主函数如下:
int main()
{
cout << fib1(45) << endl;
cout << fib2(45) << endl;
cout << fib3(45) << endl;
cout << fib4(45) << endl;
cout << fib5(45) << endl;
return 0;
}
函数fib1会等待好久,其它的都能很快得出结果,并且相同为:1134903170。
而后面两种只有在n = 1000000000的时候会显示出优势。由于我的程序都没有涉及到高精度,所以要是求大数据的话,可以通过取模来获得结果的后4位来测试效率与正确性。
另外斐波那契数列在实际工作中应该用的很少,尤其是当数据n很大的时候(例如:1000000000),所以综合考虑基本普通的非递归O(n)方法就很好了,没有必要用矩阵乘法。
附录:
程序全部源码:
#include <iostream>
#include <vector>
#include <string>
#include <cmath>
#include <fstream>
using namespace std;
class Matrix
{
public:
long matr[2][2];
Matrix(const Matrix&rhs);
Matrix(long a, long b, long c, long d);
Matrix& operator=(const Matrix&);
friend Matrix operator*(const Matrix& lhs, const Matrix& rhs)
{
Matrix ret(0,0,0,0);
ret.matr[0][0] = lhs.matr[0][0]*rhs.matr[0][0] + lhs.matr[0][1]*rhs.matr[1][0];
ret.matr[0][1] = lhs.matr[0][0]*rhs.matr[0][1] + lhs.matr[0][1]*rhs.matr[1][1];
ret.matr[1][0] = lhs.matr[1][0]*rhs.matr[0][0] + lhs.matr[1][1]*rhs.matr[1][0];
ret.matr[1][1] = lhs.matr[1][0]*rhs.matr[0][1] + lhs.matr[1][1]*rhs.matr[1][1];
return ret;
}
};
Matrix::Matrix(long a, long b, long c, long d)
{
this->matr[0][0] = a;
this->matr[0][1] = b;
this->matr[1][0] = c;
this->matr[1][1] = d;
}
Matrix::Matrix(const Matrix &rhs)
{
this->matr[0][0] = rhs.matr[0][0];
this->matr[0][1] = rhs.matr[0][1];
this->matr[1][0] = rhs.matr[1][0];
this->matr[1][1] = rhs.matr[1][1];
}
Matrix& Matrix::operator =(const Matrix &rhs)
{
this->matr[0][0] = rhs.matr[0][0];
this->matr[0][1] = rhs.matr[0][1];
this->matr[1][0] = rhs.matr[1][0];
this->matr[1][1] = rhs.matr[1][1];
return *this;
}
Matrix power(const Matrix& m, int n)
{
if (n == 1)
return m;
if (n%2 == 0)
return power(m*m, n/2);
else
return power(m*m, n/2) * m;
}
//普通递归
long fib1(int n)
{
if (n <= 2)
{
return 1;
}
else
{
return fib1(n-1) + fib1(n-2);
}
}
/*上面的效率分析代码
long fib1(int n, int* arr)
{
arr
++;
if (n <= 1)
{
return 1;
}
else
{
return fib1(n-1, arr) + fib1(n-2, arr);
}
}
*/
long fib(int n, long a, long b, int count)
{
if (count == n)
return b;
return fib(n, b, a+b, ++count);
}
//一叉递归
long fib2(int n)
{
return fib(n, 0, 1, 1);
}
//非递归方法O(n)
long fib3 (int n)
{
long x = 0, y = 1;
for (int j = 1; j < n; j++)
{
y = x + y;
x = y - x;
}
return y;
}
//矩阵乘法O(log(n))
long fib4 (int n)
{
Matrix matrix0(1, 1, 1, 0);
matrix0 = power(matrix0, n-1);
return matrix0.matr[0][0];
}
//公式法O(1)
long fib5(int n)
{
double z = sqrt(5.0);
double x = (1 + z)/2;
double y = (1 - z)/2;
return (pow(x, n) - pow(y, n))/z + 0.5;
}
int main()
{
//n = 45时候fib1()很慢
int n = 10;
cout << fib1(n) << endl;
cout << fib2(n) << endl;
cout << fib3(n) << endl;
cout << fib4(n) << endl;
cout << fib5(n) << endl;
return 0;
}
(1)分解:在分解阶段,将数据分解为更小,更容易管理的部分
(2)求解:对每个分解出的部分进行处理(递归)
(3)合并:将每部分处理的结果进行合并
二、常用实例:
(1)归并排序
(2)二分查找
(3)幂次方
(4)斐波那契数列
(5).......
下面为代码实现:
#coding=gb2312 import unittest import random import bisect ############################# # 算法学习:分治法 # 作者:chuanchuan608 # 时间: 2014/11/1 ############################# # Example 1 MergeSort start def MergeSort(L): if len(L) < 2: return L[:] else: # divide middle = len(L)>>1; # attention # Conqure left = MergeSort(L[:middle]) right = MergeSort(L[middle:]) # Combine together = Merge(left, right) return together def Merge(left, right): # alloc space to store result result = [] i, j = 0, 0 while i < len(left) and j < len(right): # compare the first two element,which is the small one, # of each two sublists if left[i] <= right[j]: result.append(left[i]) i = i + 1 else: result.append(right[j]) j = j + 1 while (i < len(left)): result.append(left[i]) i = i + 1 while (j < len(right)): result.append(right[j]) j = j + 1 return result # Example 1 MergeSort end ############################################################ # binarySearch def BinarySearch(L, e, left, right): # divide #if right < left: # return 0 if right - left < 2: if L[left] == e: return left if L[right] == e: return right return 0 # 未找到,主要针对测试用例设置bisect 未找到返回0 mid = left + (right - left)>>1 # conqure if L[mid] > e: return BinarySearch(L, e, left, mid - 1) elif L[mid] < e: return BinarySearch(L, e, mid + 1, right) elif L[mid] == e: return mid def Serach(L, e): return BinarySearch(L, e, 0, len(L) - 1) ############################################################# # PowData x^n = x*x*x*x...*x ; O(n)----DCC----->O(lg(n)) ############################################################# def PowData(X, N): import sys if N < 0: sys.exit(1) if 0 == X: return X if 0 == N: return 1 if 1 == N: return X else: if 0 == (N % 2): return PowData(X, N>>1) * PowData(X, N>>1) else: return PowData(X, (N - 1)>>1) * PowData(X, (N - 1)>>1) * X class test(unittest.TestCase): testLst = [] def test_mergesort(self): testExampleOne = [random.randrange(0, 10000000) for _ in range(10000000)] self.assertEqual(MergeSort(testExampleOne), sorted(testExampleOne)) self.assertEqual(PowData(2, 10), pow(2, 10)) if __name__ == '__main__': print(Serach([1, 2, 5, 1000], 1000) == bisect.bisect_left([1, 2, 5, 1000], 1000)) unittest.main()
而斐波那契数列的算法分析,通过幂次方的方法使得算法复杂度从指数级转向对数级。下面为转载一篇斐波那契数列的算法分析:
http://www.cnblogs.com/CCBB/archive/2011/09/14/1443441.html,该作者分析的非常详细和全面。
斐波那契数列算法分析
背景:
假定你有一雄一雌一对刚出生的兔子,它们在长到一个月大小时开始交配,在第二月结束时,雌兔子产下另一对兔子,过了一个月后它们也开始繁殖,如此这般持续下去。每只雌兔在开始繁殖时每月都产下一对兔子,假定没有兔子死亡,在一年后总共会有多少对兔子?
在一月底,最初的一对兔子交配,但是还只有1对兔子;在二月底,雌兔产下一对兔子,共有2对兔子;在三月底,最老的雌兔产下第二对兔子,共有3对兔子;在四月底,最老的雌兔产下第三对兔子,两个月前生的雌兔产下一对兔子,共有5对兔子;……如此这般计算下去,兔子对数分别是:1,
1, 2, 3, 5, 8, 13, 21, 34, 55,89, 144, ...看出规律了吗?从第3个数目开始,每个数目都是前面两个数目之和。这就是著名的斐波那契(Fibonacci)数列。
有趣问题:
1,有一段楼梯有10级台阶,规定每一步只能跨一级或两级,要登上第10级台阶有几种不同的走法?
答:这就是一个斐波那契数列:登上第一级台阶有一种登法;登上两级台阶,有两种登法;登上三级台阶,有三种登法;登上四级台阶,有五种方法……所以,1,2,3,5,8,13……登上十级,有89种。
2,数列中相邻两项的前项比后项的极限是多少,就是问,当n趋于无穷大时,F(n)/F(n+1)的极限是多少?
答:这个可由它的通项公式直接得到,极限是(-1+√5)/2,这个就是所谓的黄金分割点,也是代表大自然的和谐的一个数字。
数学表示:
Fibonacci数列的数学表达式就是:
F(n) = F(n-1) + F(n-2)
F(1) = 1
F(2) = 1
递归程序1:
Fibonacci数列可以用很直观的二叉递归程序来写,用C++语言的描述如下:
long fib1(int n)
{
if (n <= 2)
{
return 1;
}
else
{
return fib1(n-1) + fib1(n-2);
}
}
看上去程序的递归使用很恰当,可是在用VC2005的环境下测试n=37的时候用了大约3s,而n=45的时候基本下楼打完饭也看不到结果……显然这种递归的效率太低了!!
递归效率分析:
例如,用下面一个测试函数:
long fib1(int n, int* arr)
{
arr
++;
if (n <= 2)
{
return 1;
}
else
{
return fib1(n-1, arr) + fib1(n-2, arr);
}
}
这时,可以得到每个fib(i)被计算的次数:
fib(10) = 1 fib(9) = 1 fib(8) = 2 fib(7) = 3
fib(6) = 5 fib(5) = 8 fib(4) = 13 fib(3) = 21
fib(2) = 34 fib(1) = 55 fib(0) = 34
可见,计算次数呈反向的Fibonacci数列,这显然造成了大量重复计算。
我们令T(N)为函数fib(n)的运行时间,当N>=2的时候我们分析可知:
T(N) = T(N-1) + T(N-2) + 2
而fib(n) = fib(n-1) + fib(n-2),所以有T(N) >= fib(n),归纳法证明可得:
fib(N) < (5/3)^N
当N>4时,fib(N)>=
(3/2)^N
标准写法:
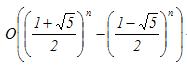
显然这个O((3/2)^N) 是以指数增长的算法,基本上是最坏的情况。
其实,这违反了递归的一个规则:合成效益法则。
合成效益法则(Compound interest rule):在求解一个问题的同一实例的时候,切勿在不同的递归调用中做重复性的工作。
所以在上面的代码中调用fib(N-1)的时候实际上同时计算了fib(N-2)。这种小的重复计算在递归过程中就会产生巨大的运行时间。
递归程序2:
用一叉递归程序就可以得到近似线性的效率,用C++语言的描述如下:
long fib(int n, long a, long b, int count)
{
if (count == n)
return b;
return fib(n, b, a+b, ++count);
}
long fib2(int n)
{
return fib(n, 0, 1, 1);
}
这种方法虽然是递归了,但是并不直观,而且效率上相比下面的迭代循环并没有优势。
迭代解法:
Fibonacci数列用迭代程序来写也很容易,用C++语言的描述如下:
//也可以用数组将每次计算的f(n)存储下来,用来下次计算用(空间换时间)
long fib3 (int n)
{
long x = 0, y = 1;
for (int j = 1; j < n; j++)
{
y = x + y;
x = y - x;
}
return y;
}
这时程序的效率显然为O(N),N
= 45的时候<1s就能得到结果。
矩阵乘法:
我们将数列写成:
Fibonacci[0] = 0,Fibonacci[1] = 1
Fibonacci
= Fibonacci[n-1] + Fibonacci[n-2] (n >= 2)
可以将它写成矩阵乘法形式:
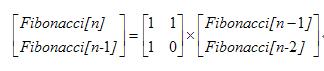
将右边连续的展开就得到:
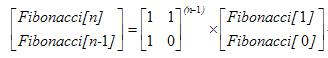
下面就是要用O(log(n))的算法计算:

显然用二分法来求,结合一些面向对象的概念,C++代码如下:
class Matrix
{
public:
long matr[2][2];
Matrix(const Matrix&rhs);
Matrix(long a, long b, long c, long d);
Matrix& operator=(const Matrix&);
friend Matrix operator*(const Matrix& lhs, const Matrix& rhs)
{
Matrix ret(0,0,0,0);
ret.matr[0][0] = lhs.matr[0][0]*rhs.matr[0][0] + lhs.matr[0][1]*rhs.matr[1][0];
ret.matr[0][1] = lhs.matr[0][0]*rhs.matr[0][1] + lhs.matr[0][1]*rhs.matr[1][1];
ret.matr[1][0] = lhs.matr[1][0]*rhs.matr[0][0] + lhs.matr[1][1]*rhs.matr[1][0];
ret.matr[1][1] = lhs.matr[1][0]*rhs.matr[0][1] + lhs.matr[1][1]*rhs.matr[1][1];
return ret;
}
};
Matrix::Matrix(long a, long b, long c, long d)
{
this->matr[0][0] = a;
this->matr[0][1] = b;
this->matr[1][0] = c;
this->matr[1][1] = d;
}
Matrix::Matrix(const Matrix &rhs)
{
this->matr[0][0] = rhs.matr[0][0];
this->matr[0][1] = rhs.matr[0][1];
this->matr[1][0] = rhs.matr[1][0];
this->matr[1][1] = rhs.matr[1][1];
}
Matrix& Matrix::operator =(const Matrix &rhs)
{
this->matr[0][0] = rhs.matr[0][0];
this->matr[0][1] = rhs.matr[0][1];
this->matr[1][0] = rhs.matr[1][0];
this->matr[1][1] = rhs.matr[1][1];
return *this;
}
Matrix power(const Matrix& m, int n)
{
if (n == 1)
return m;
if (n%2 == 0)
return power(m*m, n/2);
else
return power(m*m, n/2) * m;
}
long fib4 (int n)
{
Matrix matrix0(1, 1, 1, 0);
matrix0 = power(matrix0, n-1);
return matrix0.matr[0][0];
}
这时程序的效率为O(log(N)) 。
公式解法:
在O(1)的时间就能求得到F(n)了:
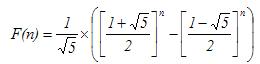
注意:其中[x]表示取距离x最近的整数。
用C++写的代码如下:
long fib5(int n)
{
double z = sqrt(5.0);
double x = (1 + z)/2;
double y = (1 - z)/2;
return (pow(x, n) - pow(y, n))/z + 0.5;
}
这个与数学库实现开方和乘方本身效率有关的,我想应该还是在O(log(n))的效率。
总结:
上面给出了5中求解斐波那契数列的方法,用测试程序主函数如下:
int main()
{
cout << fib1(45) << endl;
cout << fib2(45) << endl;
cout << fib3(45) << endl;
cout << fib4(45) << endl;
cout << fib5(45) << endl;
return 0;
}
函数fib1会等待好久,其它的都能很快得出结果,并且相同为:1134903170。
而后面两种只有在n = 1000000000的时候会显示出优势。由于我的程序都没有涉及到高精度,所以要是求大数据的话,可以通过取模来获得结果的后4位来测试效率与正确性。
另外斐波那契数列在实际工作中应该用的很少,尤其是当数据n很大的时候(例如:1000000000),所以综合考虑基本普通的非递归O(n)方法就很好了,没有必要用矩阵乘法。
附录:
程序全部源码:
#include <iostream>
#include <vector>
#include <string>
#include <cmath>
#include <fstream>
using namespace std;
class Matrix
{
public:
long matr[2][2];
Matrix(const Matrix&rhs);
Matrix(long a, long b, long c, long d);
Matrix& operator=(const Matrix&);
friend Matrix operator*(const Matrix& lhs, const Matrix& rhs)
{
Matrix ret(0,0,0,0);
ret.matr[0][0] = lhs.matr[0][0]*rhs.matr[0][0] + lhs.matr[0][1]*rhs.matr[1][0];
ret.matr[0][1] = lhs.matr[0][0]*rhs.matr[0][1] + lhs.matr[0][1]*rhs.matr[1][1];
ret.matr[1][0] = lhs.matr[1][0]*rhs.matr[0][0] + lhs.matr[1][1]*rhs.matr[1][0];
ret.matr[1][1] = lhs.matr[1][0]*rhs.matr[0][1] + lhs.matr[1][1]*rhs.matr[1][1];
return ret;
}
};
Matrix::Matrix(long a, long b, long c, long d)
{
this->matr[0][0] = a;
this->matr[0][1] = b;
this->matr[1][0] = c;
this->matr[1][1] = d;
}
Matrix::Matrix(const Matrix &rhs)
{
this->matr[0][0] = rhs.matr[0][0];
this->matr[0][1] = rhs.matr[0][1];
this->matr[1][0] = rhs.matr[1][0];
this->matr[1][1] = rhs.matr[1][1];
}
Matrix& Matrix::operator =(const Matrix &rhs)
{
this->matr[0][0] = rhs.matr[0][0];
this->matr[0][1] = rhs.matr[0][1];
this->matr[1][0] = rhs.matr[1][0];
this->matr[1][1] = rhs.matr[1][1];
return *this;
}
Matrix power(const Matrix& m, int n)
{
if (n == 1)
return m;
if (n%2 == 0)
return power(m*m, n/2);
else
return power(m*m, n/2) * m;
}
//普通递归
long fib1(int n)
{
if (n <= 2)
{
return 1;
}
else
{
return fib1(n-1) + fib1(n-2);
}
}
/*上面的效率分析代码
long fib1(int n, int* arr)
{
arr
++;
if (n <= 1)
{
return 1;
}
else
{
return fib1(n-1, arr) + fib1(n-2, arr);
}
}
*/
long fib(int n, long a, long b, int count)
{
if (count == n)
return b;
return fib(n, b, a+b, ++count);
}
//一叉递归
long fib2(int n)
{
return fib(n, 0, 1, 1);
}
//非递归方法O(n)
long fib3 (int n)
{
long x = 0, y = 1;
for (int j = 1; j < n; j++)
{
y = x + y;
x = y - x;
}
return y;
}
//矩阵乘法O(log(n))
long fib4 (int n)
{
Matrix matrix0(1, 1, 1, 0);
matrix0 = power(matrix0, n-1);
return matrix0.matr[0][0];
}
//公式法O(1)
long fib5(int n)
{
double z = sqrt(5.0);
double x = (1 + z)/2;
double y = (1 - z)/2;
return (pow(x, n) - pow(y, n))/z + 0.5;
}
int main()
{
//n = 45时候fib1()很慢
int n = 10;
cout << fib1(n) << endl;
cout << fib2(n) << endl;
cout << fib3(n) << endl;
cout << fib4(n) << endl;
cout << fib5(n) << endl;
return 0;
}
相关文章推荐
- 算法学习--分治法
- 本文专注于<递归算法和分治思想>[胖虎学习算法系列]
- 算法设计技巧和分析学习笔记1 (归纳法、分治和动态规划)
- 算法分析之分治法学习总结(一)
- 算法学习之路:分治策略-最大子数组-java实现
- 【从零学习经典算法系列】分治与递归1——递归表达式与解法初步
- 【算法学习】最大子数组问题的分治法求解
- 【算法学习】归并排序——基于分治思想
- 算法学习笔记(五)------归并排序(分治)
- 算法学习之分治--快速排序
- 本文专注于<递归算法和分治思想>[胖虎学习算法系列]
- java基础算法学习之分治
- 算法分析之分治法学习总结(一)
- 算法学习之路:分治策略-归并排序-java实现
- 算法学习2 - 分治
- 算法学习之分治策略-最大子数组
- 经典算法学习-循坏赛日程表-分治|递推|压位lowbit
- 递归与分治算法初步学习
- 【从零学习经典算法系列】分治与递归2——主方法
- 算法学习之旅,中级篇(8)-–分治之二分搜索(递归)
