逻辑回归和牛顿法 Logistic Regression and Newton's Method
2014-10-19 21:12
459 查看
英文
中文
训练数据:
共80个学生的两门课成绩。根据两门成绩,40名学生可以上大学,另外40名学生不能上大学。训练集由向量X和Y组成。X为80行*2列,每行表示一个学生,第1列表示第1门课成绩,第2例表示第2门课成绩。Y为80行*1列,1列值为1表示可以上大学,值为0表示不能上大学。
% Exercise 4 -- Logistic Regression
clear all; close all; clc
x = load('ex4x.dat'); %x:80*2, 2个特征
y = load('ex4y.dat'); %y:80*1
[m, n] = size(x); %m:80, n:2
% Add intercept term to x
x = [ones(m, 1), x]; %x:80*3, 设X0 = 1
% Plot the training data
% Use different markers for positives and negatives
figure
pos = find(y==1);%y中元素值等于1的所有下标
neg = find(y == 0);
plot(x(pos, 2), x(pos,3), '+') %分别表示可以上大学的同学第1门成绩、第2门成绩
hold on
plot(x(neg, 2), x(neg, 3), 'o') %分别表示不能上大学的同学第1门成绩、第2门成绩
hold on
xlabel('Exam 1 score')
ylabel('Exam 2 score')
% Initialize fitting parameters
theta = zeros(n+1, 1); % 3*1
% Define the sigmoid function 定义一个内置函数g,参数是z
g = inline('1.0 ./ (1.0 + exp(-z))');
% Newton's method 牛顿法
MAX_ITR = 7; %牛顿法通过迭代次数5-15次就收敛了
J = zeros(MAX_ITR, 1); %成本函数初始值为0
for i = 1:MAX_ITR
% Calculate the hypothesis function
z = x * theta; % 80*1
h = g(z);
% Calculate gradient and hessian.
% The formulas below are equivalent to the summation formulas
% given in the lecture videos.
grad = (1/m).*x' * (h-y); %梯度的矢量表示
H = (1/m).*x' * diag(h) * diag(1-h) * x; %H的矢量表示
% Calculate J (for testing convergence) 成本函数
J(i) =(1/m)*sum(-y.*log(h) - (1-y).*log(1-h));
theta = theta - H\grad; %theta迭代公式
end
% Display theta
theta
% Calculate the probability that a student with
% Score 20 on exam 1 and score 80 on exam 2
% will not be admitted 通过这个学生成绩计算概率值, g函数值大于0.5就能上大学
prob = 1- g([1, 20, 80]*theta) %不能上的概率
% Plot Newton's method result
% Only need 2 points to define a line, so choose two endpoints 线画长一点
plot_x = [min(x(:,2))-2, max(x(:,2)+2)];
% Calculate the decision boundary line 分界线
%令函数g的值0.5,可推出theta'X=0,满足这个方程的点就是分界线,即:
%theta(1)*1+theta(2)*plot_x+theta(3)*plot_y=0,解出plot_y即可。
%plot_x,plot_y分别表示成绩1、成绩2
plot_y = (-1./theta(3)).*(theta(2).*plot_x +theta(1));
plot(plot_x, plot_y)
legend('Admitted', 'Not admitted', 'Decision Boundary')
hold off
% Plot J
figure
plot(0:MAX_ITR-1, J, 'o--', 'MarkerFaceColor', 'r', 'MarkerSize', 8)
xlabel('Iteration'); ylabel('J')
% Display J
J
结果分析:
采用牛顿法经过5次迭代成本函数J就可以收敛了。第4次和第5次迭代的结果差已经小于
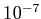
采用梯度下降法可能需要上百或上千次,函数才能收敛。因此,牛顿法收敛速度很快。
中文
训练数据:
共80个学生的两门课成绩。根据两门成绩,40名学生可以上大学,另外40名学生不能上大学。训练集由向量X和Y组成。X为80行*2列,每行表示一个学生,第1列表示第1门课成绩,第2例表示第2门课成绩。Y为80行*1列,1列值为1表示可以上大学,值为0表示不能上大学。
% Exercise 4 -- Logistic Regression
clear all; close all; clc
x = load('ex4x.dat'); %x:80*2, 2个特征
y = load('ex4y.dat'); %y:80*1
[m, n] = size(x); %m:80, n:2
% Add intercept term to x
x = [ones(m, 1), x]; %x:80*3, 设X0 = 1
% Plot the training data
% Use different markers for positives and negatives
figure
pos = find(y==1);%y中元素值等于1的所有下标
neg = find(y == 0);
plot(x(pos, 2), x(pos,3), '+') %分别表示可以上大学的同学第1门成绩、第2门成绩
hold on
plot(x(neg, 2), x(neg, 3), 'o') %分别表示不能上大学的同学第1门成绩、第2门成绩
hold on
xlabel('Exam 1 score')
ylabel('Exam 2 score')
% Initialize fitting parameters
theta = zeros(n+1, 1); % 3*1
% Define the sigmoid function 定义一个内置函数g,参数是z
g = inline('1.0 ./ (1.0 + exp(-z))');
% Newton's method 牛顿法
MAX_ITR = 7; %牛顿法通过迭代次数5-15次就收敛了
J = zeros(MAX_ITR, 1); %成本函数初始值为0
for i = 1:MAX_ITR
% Calculate the hypothesis function
z = x * theta; % 80*1
h = g(z);
% Calculate gradient and hessian.
% The formulas below are equivalent to the summation formulas
% given in the lecture videos.
grad = (1/m).*x' * (h-y); %梯度的矢量表示
H = (1/m).*x' * diag(h) * diag(1-h) * x; %H的矢量表示
% Calculate J (for testing convergence) 成本函数
J(i) =(1/m)*sum(-y.*log(h) - (1-y).*log(1-h));
theta = theta - H\grad; %theta迭代公式
end
% Display theta
theta
% Calculate the probability that a student with
% Score 20 on exam 1 and score 80 on exam 2
% will not be admitted 通过这个学生成绩计算概率值, g函数值大于0.5就能上大学
prob = 1- g([1, 20, 80]*theta) %不能上的概率
% Plot Newton's method result
% Only need 2 points to define a line, so choose two endpoints 线画长一点
plot_x = [min(x(:,2))-2, max(x(:,2)+2)];
% Calculate the decision boundary line 分界线
%令函数g的值0.5,可推出theta'X=0,满足这个方程的点就是分界线,即:
%theta(1)*1+theta(2)*plot_x+theta(3)*plot_y=0,解出plot_y即可。
%plot_x,plot_y分别表示成绩1、成绩2
plot_y = (-1./theta(3)).*(theta(2).*plot_x +theta(1));
plot(plot_x, plot_y)
legend('Admitted', 'Not admitted', 'Decision Boundary')
hold off
% Plot J
figure
plot(0:MAX_ITR-1, J, 'o--', 'MarkerFaceColor', 'r', 'MarkerSize', 8)
xlabel('Iteration'); ylabel('J')
% Display J
J
结果分析:
采用牛顿法经过5次迭代成本函数J就可以收敛了。第4次和第5次迭代的结果差已经小于
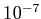
采用梯度下降法可能需要上百或上千次,函数才能收敛。因此,牛顿法收敛速度很快。
相关文章推荐
- 机器学习2——分类和逻辑回归Classification and logistic regression(牛顿法待研究)
- Logistic and Softmax Regression (逻辑回归和Softmax回归)
- 斯坦福CS229机器学习课程笔记 part2:分类和逻辑回归 Classificatiion and logistic regression
- Exercise: Logistic Regression and Newton's Method
- Logistic and Softmax Regression (逻辑回归和Softmax回归)
- [机器学习实验3]Logistic Regression and Newton Method
- 逻辑回归(Logistic+Regression)
- Newton's method and Quasi Newton method牛顿法与拟牛顿法
- Stanford机器学习---第三讲. 逻辑回归和过拟合问题的解决 logistic Regression & Regularization
- Spark LogisticRegression 逻辑回归之建模
- Coursera DeepLearning.ai Logistic Regression逻辑回归总结
- 第三讲. 逻辑回归和过拟合问题的解决 logistic Regression & Regularization
- Matlab实现线性回归和逻辑回归: Linear Regression & Logistic Regression
- Stanford机器学习网络课程---第三讲. 逻辑回归和过拟合问题的解决 logistic Regression & Regularization
- 【转载】Stanford机器学习---第三讲. 逻辑回归和过拟合问题的解决 logistic Regression & Regularization
- Stanford机器学习网络课程---第三讲(续)Matlab实现线性回归和逻辑回归: Linear Regression & Logistic Regression
- MachineLearning—Logistic Regression(四)-逻辑回归应用于手写数字识别
- Stanford机器学习---第三讲. 逻辑回归和过拟合问题的解决 logistic Regression & Regularization
- Stanford机器学习---第三讲. 逻辑回归和过拟合问题的解决 logistic Regression & Regularization
- Stanford机器学习---第三讲. 逻辑回归和过拟合问题的解决 logistic Regression & Regularization
