红黑树
2014-09-07 11:15
337 查看
红黑树(RBT)的定义:它或者是一颗空树,或者是具有一下性质的二叉查找树:
1.节点非红即黑。
2.根节点是黑色。
3.所有NULL结点称为叶子节点,且认为颜色为黑。
4.所有红节点的子节点都为黑色。
5.从任一节点到其叶子节点的所有路径上都包含相同数目的黑节点。

所有性质1-5合起来约束了该树的平衡性能--即该树上的最长路径不可能会大于2倍最短路径。为什么?因为第1条该树上的节点非红即黑,由于第4条该树上不允许存在两个连续的红节点,那么对于从一个节点到其叶子节点的一条最长的路径一定是红黑交错的,那么最短路径一定是纯黑色的节点;而又第5条从任一节点到其叶子节点的所有路径上都包含相同数目的黑节点,这么来说最长路径上的黑节点的数目和最短路径上的黑节点的数目相等!而又第2条根结点为黑、第3条叶子节点是黑,那么可知:最长路径<=2*最短路径。一颗二叉树的平衡性能越好,那么它的效率越高!显然红黑树的平衡性能比AVL的略差些,但是经过大量试验证明,实际上红黑树的效率还是很不错了,仍能达到O(logN)。
插入操作
由于性质的约束:插入点不能为黑节点,应插入红节点。因为你插入黑节点将破坏性质5,所以每次插入的点都是红结点,但是若他的父节点也为红,那岂不是破坏了性质4?对啊,所以要做一些“旋转”和一些节点的变色!另为叙述方便我们给要插入的节点标为N(红色),父节点为P,祖父节点为G,叔节点为U。下边将一一列出所有插入时遇到的情况:
情形1:该树为空树,直接插入根结点的位置,违反性质1,把节点颜色有红改为黑即可。
情形2:插入节点N的父节点P为黑色,不违反任何性质,无需做任何修改。
情形1很简单,情形2中P为黑色,一切安然无事,但P为红就不一样了,下边是P为红的各种情况,也是真正要学的地方!
情形3:N为红,P为红,(祖节点一定存在,且为黑,下边同理)U也为红,这里不论P是G的左孩子,还是右孩子;不论N是P的左孩子,还是右孩子。

操作:如图把P、U改为黑色,G改为红色,未结束。
解析:N、P都为红,违反性质4;若把P改为黑,符合性质4,显然左边少了一个黑节点,违反性质5;所

以我们把G,U都改为相反色,这样一来通过G的路径的黑节点数目没变,即符合4、5,但是G变红了,若G的父节点又是红的不就有违反了4,是这样,所以经过上边操作后未结束,需把G作为起始点,即把G看做一个插入的红节点继续向上检索----属于哪种情况,按那种情况操作~要么中间就结束,要么知道根结点(此时根结点变红,一根结点向上检索,那木有了,那就把他变为黑色吧)。
情形4:N为红,P为红,U为黑,P为G的左孩子,N为P的左孩子(或者P为G的右孩子,N为P的左孩子;反正就是同向的)。

操作:如图P、G变色,P、G变换即左左单旋(或者右右单旋),结束。
解析:要知道经过P、G变换(旋转),变换后P的位置就是当年G的位置,所以红P变为黑,而黑G变为红都是为了不违反性质5,而维持到达叶节点所包含的黑节点的数目不变!还可以理解为:也就是相当于(只是相当于,并不是实事,只是为了更好理解;)把红N头上的红节点移到对面黑U的头上;这样即符合了性质4也不违反性质5,这样就结束了。
情形5:N为红,P为红,U为黑,P为G的左孩子,N为P的右孩子(或者P为G的右孩子,N为P的左孩子;反正两方向相反)。

操作:需要进行两次变换(旋转),图中只显示了一次变换-----首先P、N变换,颜色不变;然后就变成了情形4的情况,按照情况4操作,即结束。
解析:由于P、N都为红,经变换,不违反性质5;然后就变成4的情形,此时G与G现在的左孩子变色,并变换,结束。
删除操作
我们知道删除需先找到“替代点”来替代删除点而被删除,也就是删除的是替代点,而替代点N的至少有一个子节点为NULL,那么,若N为红色,则两个子节点一定都为NULL(必须地),那么直接把N删了,不违反任何性质,ok,结束了;若N为黑色,另一个节点M不为NULL,则另一个节点M一定是红色的,且M的子节点都为NULL(按性质来的,不明白,自己分析一下)那么把N删掉,M占到N的位置,并改为黑色,不违反任何性质,ok,结束了;若N为黑色,另一个节点也为NULL,则把N删掉,该位置置为NULL,显然这个黑节点被删除了,破坏了性质5,那么要以N节点为起始点检索看看属于那种情况,并作相应的操作,另还需说明N为黑点(也许是NULL,也许不是,都一样),P为父节点,S为兄弟节点(这个我真想给兄弟节点叫B(brother)多好啊,不过人家图就是S我也不能改,在重画图,太浪费时间了!S也行呵呵,就当是sister也行,哈哈)分为以下5中情况:
情形1:S为红色(那么父节点P一定是黑,子节点一定是黑),N是P的左孩子(或者N是P的右孩子)。

操作:P、S变色,并交换----相当于AVL中的右右中旋转即以P为中心S向左旋(或者是AVL中的左左中的旋转),未结束。
解析:我们知道P的左边少了一个黑节点,这样操作相当于在N头上又加了一个红节点----不违反任何性质,但是到通过N的路径仍少了一个黑节点,需要再把对N进行一次检索,并作相应的操作才可以平衡(暂且不管往下看)。
情形2:P、S及S的孩子们都为黑。

操作:S改为红色,未结束。
解析:S变为红色后经过S节点的路径的黑节点数目也减少了1,那个从P出发到其叶子节点到所有路径所包含的黑节点数目(记为num)相等了。但是这个num比之前少了1,因为左右子树中的黑节点数目都减少了!一般地,P是他父节点G的一个孩子,那么由G到其叶子节点的黑节点数目就不相等了,所以说没有结束,需把P当做新的起始点开始向上检索。
情形3:P为红(S一定为黑),S的孩子们都为黑。

操作:P该为黑,S改为红,结束。
解析:这种情况最简单了,既然N这边少了一个黑节点,那么S这边就拿出了一个黑节点来共享一下,这样一来,S这边没少一个黑节点,而N这边便多了一个黑节点,这样就恢复了平衡,多么美好的事情哈!
情形4:P任意色,S为黑,N是P的左孩子,S的右孩子SR为红,S的左孩子任意(或者是N是P的右孩子,S的左孩子为红,S的右孩子任意)。

操作:SR(SL)改为黑,P改为黑,S改为P的颜色,P、S变换--这里相对应于AVL中的右右中的旋转(或者是AVL中的左左旋转),结束。
解析:P、S旋转有变色,等于给N这边加了一个黑节点,P位置(是位置而不是P)的颜色不变,S这边少了一个黑节点;SR有红变黑,S这边又增加了一个黑节点;这样一来又恢复了平衡,结束。
情形5:P任意色,S为黑,N是P的左孩子,S的左孩子SL为红,S的右孩子SR为黑(或者N是P的有孩子,S的右孩子为红,S的左孩子为黑)。

操作:SL(或SR)改为黑,S改为红,SL(SR)、S变换;此时就回到了情形4,SL(SR)变成了黑S,S变成了红SR(SL),做情形4的操作即可,这两次变换,其实就是对应AVL的右左的两次旋转(或者是AVL的左右的两次旋转)。
解析:这种情况如果你按情形4的操作的话,由于SR本来就是黑色,你无法弥补由于P、S的变换(旋转)给S这边造成的损失!所以我没先对S、SL进行变换之后就变为情形4的情况了,何乐而不为呢?
树的旋转知识
当我们在对红黑树进行插入和删除等操作时,对树做了修改,那么可能会违背红黑树的性质。
为了保持红黑树的性质,我们可以通过对树进行旋转,即修改树种某些结点的颜色及指针结构,以达到对红黑树进行
插入、删除结点等操作时,红黑树依然能保持它特有的性质(如上文所述的,五点性质)。
树的旋转,分为左旋和右旋,以下借助图来做形象的解释和介绍:
1.左旋
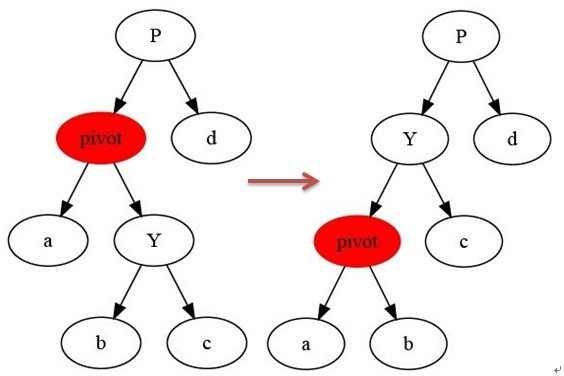
如上图所示:
当在某个结点pivot上,做左旋操作时,我们假设它的右孩子y不是NIL[T],pivot可以为树内任意右孩子而不是NIL[T]的结点。
左旋以pivot到y之间的链为“支轴”进行,它使y成为该孩子树新的根,而y的左孩子b则成为pivot的右孩子。
来看算法导论对此操作的算法实现(以x代替上述的pivot):
LEFT-ROTATE(T, x)
1 y ← right[x] ▹ Set y.
2 right[x] ← left[y] ▹ Turn y's
left subtree into x's right subtree.
3 p[left[y]] ← x
4 p[y] ← p[x] ▹ Link x's
parent to y.
5 if p[x] = nil[T]
6 then root[T] ← y
7 else if x = left[p[x]]
8 then left[p[x]] ← y
9 else right[p[x]] ← y
10 left[y] ← x ▹ Put x on y's
left.
11 p[x] ← y
2.右旋
右旋与左旋差不多,再此不做详细介绍。

对于树的旋转,能保持不变的只有原树的搜索性质,而原树的红黑性质则不能保持,
在红黑树的数据插入和删除后可利用旋转和颜色重涂来恢复树的红黑性质。
至于有些书如 STL源码剖析有对双旋的描述,其实双旋只是单旋的两次应用,并无新的内容,
因此这里就不再介绍了,而且左右旋也是相互对称的,只要理解其中一种旋转就可以了。
三、红黑树插入、删除操作的具体实现
三、I、ok,接下来,咱们来具体了解红黑树的插入操作。
向一棵含有n个结点的红黑树插入一个新结点的操作可以在O(lgn)时间内完成。
算法导论:
RB-INSERT(T, z)
1 y ← nil[T]
2 x ← root[T]
3 while x ≠ nil[T]
4 do y ← x
5 if key[z] < key[x]
6 then x ← left[x]
7 else x ← right[x]
8 p[z] ← y
9 if y = nil[T]
10 then root[T] ← z
11 else if key[z] < key[y]
12 then left[y] ← z
13 else right[y] ← z
14 left[z] ← nil[T]
15 right[z] ← nil[T]
16 color[z] ← RED
17 RB-INSERT-FIXUP(T, z)
咱们来具体分析下,此段代码:
RB-INSERT(T, z),将z插入红黑树T 之内。
为保证红黑性质在插入操作后依然保持,上述代码调用了一个辅助程序RB-INSERT-FIXUP
来对结点进行重新着色,并旋转。
14 left[z] ← nil[T]
15 right[z] ← nil[T] //保持正确的树结构
第16行,将z着为红色,由于将z着为红色可能会违背某一条红黑树的性质,
所以,在第17行,调用RB-INSERT-FIXUP(T,z)来保持红黑树的性质。
RB-INSERT-FIXUP(T, z),如下所示:
1 while color[p[z]] = RED
2 do if p[z] = left[p[p[z]]]
3 then y ← right[p[p[z]]]
4 if color[y] = RED
5 then color[p[z]] ← BLACK ▹ Case 1
6 color[y] ← BLACK ▹ Case 1
7 color[p[p[z]]] ← RED ▹ Case 1
8 z ← p[p[z]] ▹ Case 1
9 else if z = right[p[z]]
10 then z ← p[z] ▹ Case 2
11 LEFT-ROTATE(T, z) ▹ Case 2
12 color[p[z]] ← BLACK ▹ Case 3
13 color[p[p[z]]] ← RED ▹ Case 3
14 RIGHT-ROTATE(T, p[p[z]]) ▹ Case 3
15 else (same as then clause
with "right" and "left" exchanged)
16 color[root[T]] ← BLACK
情况1:插入的是根结点。
原树是空树,此情况只会违反性质2。
对策:直接把此结点涂为黑色。
情况2:插入的结点的父结点是黑色。
此不会违反性质2和性质4,红黑树没有被破坏。
对策:什么也不做。
情况3:当前结点的父结点是红色且祖父结点的另一个子结点(叔叔结点)是红色。
此时父结点的父结点一定存在,否则插入前就已不是红黑树。
与此同时,又分为父结点是祖父结点的左子还是右子,对于对称性,我们只要解开一个方向就可以了。
在此,我们只考虑父结点为祖父左子的情况。
同时,还可以分为当前结点是其父结点的左子还是右子,但是处理方式是一样的。我们将此归为同一类。
对策:将当前节点的父节点和叔叔节点涂黑,祖父结点涂红,把当前结点指向祖父节点,从新的当前节点重新开始算法。
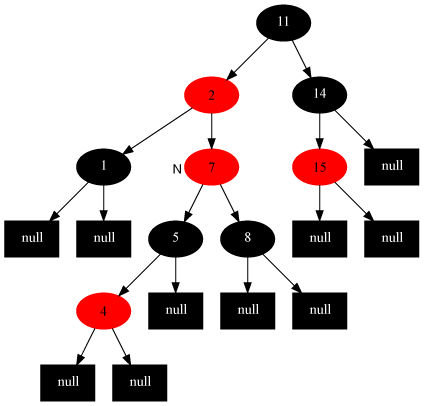
针对情况3,变化前(图片来源:saturnman)[插入4节点]:

变化后:
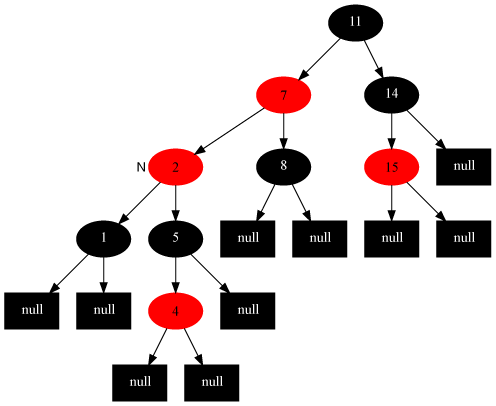
情况4:当前节点的父节点是红色,叔叔节点是黑色,当前节点是其父节点的右子
对策:当前节点的父节点做为新的当前节点,以新当前节点为支点左旋。
如下图所示,变化前[插入7节点]:

变化后:
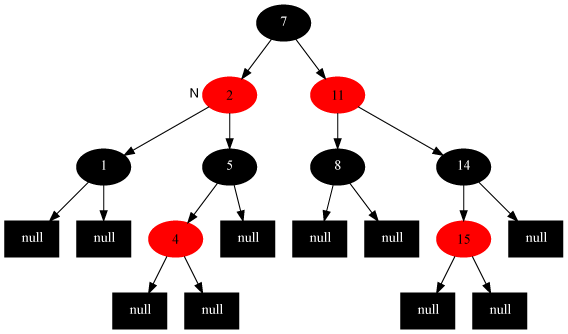
情况5:当前节点的父节点是红色,叔叔节点是黑色,当前节点是其父节点的左子
解法:父节点变为黑色,祖父节点变为红色,在祖父节点为支点右旋
如下图所示[插入2节点]

变化后:
==================
三、II、ok,接下来,咱们最后来了解,红黑树的删除操作:
算法导论一书,给的算法实现:
RB-DELETE(T, z) 单纯删除结点的总操作
1 if left[z] = nil[T] or right[z] = nil[T]
2 then y ← z
3 else y ← TREE-SUCCESSOR(z)
4 if left[y] ≠ nil[T]
5 then x ← left[y]
6 else x ← right[y]
7 p[x] ← p[y]
8 if p[y] = nil[T]
9 then root[T] ← x
10 else if y = left[p[y]]
11 then left[p[y]] ← x
12 else right[p[y]] ← x
13 if y 3≠ z
14 then key[z] ← key[y]
15 copy y's satellite data into z
16 if color[y] = BLACK
17 then RB-DELETE-FIXUP(T, x)
18 return y
RB-DELETE-FIXUP(T, x) 恢复与保持红黑性质的工作
1 while x ≠ root[T] and color[x] = BLACK
2 do if x = left[p[x]]
3 then w ← right[p[x]]
4 if color[w] = RED
5 then color[w] ← BLACK ▹ Case 1
6 color[p[x]] ← RED ▹ Case 1
7 LEFT-ROTATE(T, p[x]) ▹ Case 1
8 w ← right[p[x]] ▹ Case 1
9 if color[left[w]] = BLACK and color[right[w]] = BLACK
10 then color[w] ← RED ▹ Case 2
11 x p[x] ▹ Case 2
12 else if color[right[w]] = BLACK
13 then color[left[w]] ← BLACK ▹ Case 3
14 color[w] ← RED ▹ Case 3
15 RIGHT-ROTATE(T, w) ▹ Case 3
16 w ← right[p[x]] ▹ Case 3
17 color[w] ← color[p[x]] ▹ Case 4
18 color[p[x]] ← BLACK ▹ Case 4
19 color[right[w]] ← BLACK ▹ Case 4
20 LEFT-ROTATE(T, p[x]) ▹ Case 4
21 x ← root[T] ▹ Case 4
22 else (same as then clause with "right" and "left" exchanged)
23 color[x] ← BLACK
情况1:当前节点是红色
解法,直接把当前节点染成黑色,结束。
此时红黑树性质全部恢复。
情况2:当前节点是黑色且是根节点
解法:什么都不做,结束
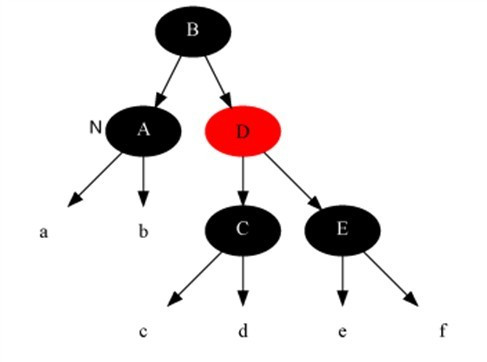
情况3:当前节点是黑色,且兄弟节点为红色(此时父节点和兄弟节点的子节点分为黑)。
解法:把父节点染成红色,把兄弟结点染成黑色,之后重新进入算法(我们只讨论当前节点是其父节点左孩子时的情况)。
然后,针对父节点做一次左旋。此变换后原红黑树性质5不变,而把问题转化为兄弟节点为黑色的情况。
3.变化前:
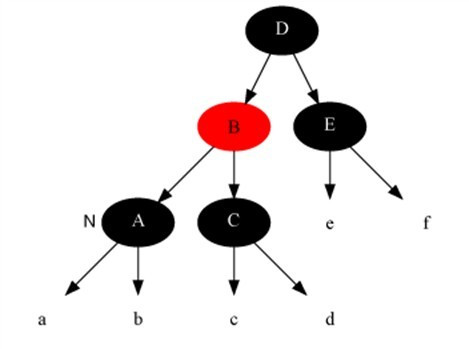
3.变化后:
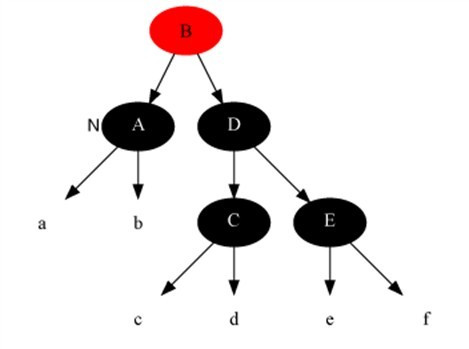
情况4:当前节点是黑色,且兄弟是黑色,且兄弟节点的两个子节点全为黑色。
解法:把当前节点和兄弟节点中抽取一重黑色追加到父节点上,把父节点当成新的当前节点,重新进入算法。(此变换后性质5不变)
4.变化前
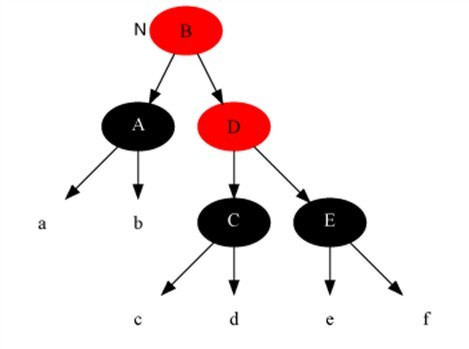
4.变化后
情况5:当前节点颜色是黑色,兄弟节点是黑色,兄弟的左子是红色,右子是黑色。
解法:把兄弟结点染红,兄弟左子节点染黑,之后再在兄弟节点为支点解右旋,
之后重新进入算法。此是把当前的情况转化为情况6,而性质5得以保持。
5.变化前:
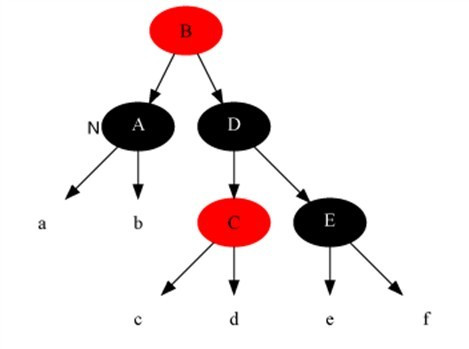
5.变化后:
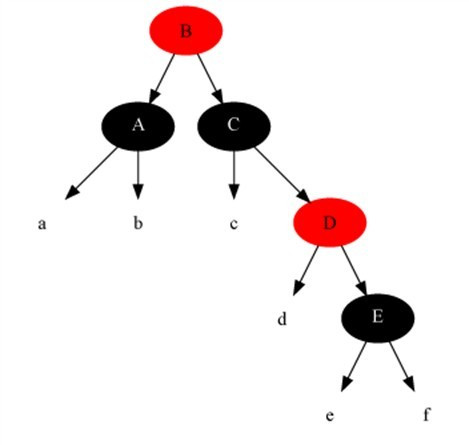
情况6:当前节点颜色是黑色,它的兄弟节点是黑色,但是兄弟节点的右子是红色,兄弟节点左子的颜色任意。
解法:把兄弟节点染成当前节点父节点的颜色,把当前节点父节点染成黑色,兄弟节点右子染成黑色,
之后以当前节点的父节点为支点进行左旋,此时算法结束,红黑树所有性质调整正确。
6.变化前:
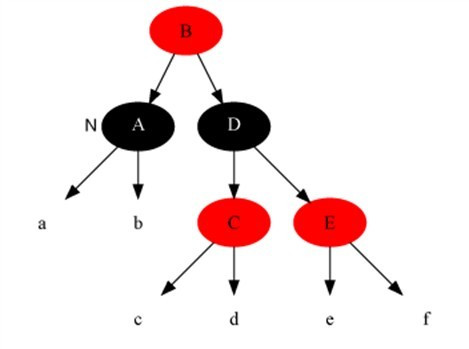
6.变化后:

1.节点非红即黑。
2.根节点是黑色。
3.所有NULL结点称为叶子节点,且认为颜色为黑。
4.所有红节点的子节点都为黑色。
5.从任一节点到其叶子节点的所有路径上都包含相同数目的黑节点。

所有性质1-5合起来约束了该树的平衡性能--即该树上的最长路径不可能会大于2倍最短路径。为什么?因为第1条该树上的节点非红即黑,由于第4条该树上不允许存在两个连续的红节点,那么对于从一个节点到其叶子节点的一条最长的路径一定是红黑交错的,那么最短路径一定是纯黑色的节点;而又第5条从任一节点到其叶子节点的所有路径上都包含相同数目的黑节点,这么来说最长路径上的黑节点的数目和最短路径上的黑节点的数目相等!而又第2条根结点为黑、第3条叶子节点是黑,那么可知:最长路径<=2*最短路径。一颗二叉树的平衡性能越好,那么它的效率越高!显然红黑树的平衡性能比AVL的略差些,但是经过大量试验证明,实际上红黑树的效率还是很不错了,仍能达到O(logN)。
插入操作
由于性质的约束:插入点不能为黑节点,应插入红节点。因为你插入黑节点将破坏性质5,所以每次插入的点都是红结点,但是若他的父节点也为红,那岂不是破坏了性质4?对啊,所以要做一些“旋转”和一些节点的变色!另为叙述方便我们给要插入的节点标为N(红色),父节点为P,祖父节点为G,叔节点为U。下边将一一列出所有插入时遇到的情况:
情形1:该树为空树,直接插入根结点的位置,违反性质1,把节点颜色有红改为黑即可。
情形2:插入节点N的父节点P为黑色,不违反任何性质,无需做任何修改。
情形1很简单,情形2中P为黑色,一切安然无事,但P为红就不一样了,下边是P为红的各种情况,也是真正要学的地方!
情形3:N为红,P为红,(祖节点一定存在,且为黑,下边同理)U也为红,这里不论P是G的左孩子,还是右孩子;不论N是P的左孩子,还是右孩子。

操作:如图把P、U改为黑色,G改为红色,未结束。
解析:N、P都为红,违反性质4;若把P改为黑,符合性质4,显然左边少了一个黑节点,违反性质5;所

以我们把G,U都改为相反色,这样一来通过G的路径的黑节点数目没变,即符合4、5,但是G变红了,若G的父节点又是红的不就有违反了4,是这样,所以经过上边操作后未结束,需把G作为起始点,即把G看做一个插入的红节点继续向上检索----属于哪种情况,按那种情况操作~要么中间就结束,要么知道根结点(此时根结点变红,一根结点向上检索,那木有了,那就把他变为黑色吧)。
情形4:N为红,P为红,U为黑,P为G的左孩子,N为P的左孩子(或者P为G的右孩子,N为P的左孩子;反正就是同向的)。

操作:如图P、G变色,P、G变换即左左单旋(或者右右单旋),结束。
解析:要知道经过P、G变换(旋转),变换后P的位置就是当年G的位置,所以红P变为黑,而黑G变为红都是为了不违反性质5,而维持到达叶节点所包含的黑节点的数目不变!还可以理解为:也就是相当于(只是相当于,并不是实事,只是为了更好理解;)把红N头上的红节点移到对面黑U的头上;这样即符合了性质4也不违反性质5,这样就结束了。
情形5:N为红,P为红,U为黑,P为G的左孩子,N为P的右孩子(或者P为G的右孩子,N为P的左孩子;反正两方向相反)。

操作:需要进行两次变换(旋转),图中只显示了一次变换-----首先P、N变换,颜色不变;然后就变成了情形4的情况,按照情况4操作,即结束。
解析:由于P、N都为红,经变换,不违反性质5;然后就变成4的情形,此时G与G现在的左孩子变色,并变换,结束。
删除操作
我们知道删除需先找到“替代点”来替代删除点而被删除,也就是删除的是替代点,而替代点N的至少有一个子节点为NULL,那么,若N为红色,则两个子节点一定都为NULL(必须地),那么直接把N删了,不违反任何性质,ok,结束了;若N为黑色,另一个节点M不为NULL,则另一个节点M一定是红色的,且M的子节点都为NULL(按性质来的,不明白,自己分析一下)那么把N删掉,M占到N的位置,并改为黑色,不违反任何性质,ok,结束了;若N为黑色,另一个节点也为NULL,则把N删掉,该位置置为NULL,显然这个黑节点被删除了,破坏了性质5,那么要以N节点为起始点检索看看属于那种情况,并作相应的操作,另还需说明N为黑点(也许是NULL,也许不是,都一样),P为父节点,S为兄弟节点(这个我真想给兄弟节点叫B(brother)多好啊,不过人家图就是S我也不能改,在重画图,太浪费时间了!S也行呵呵,就当是sister也行,哈哈)分为以下5中情况:
情形1:S为红色(那么父节点P一定是黑,子节点一定是黑),N是P的左孩子(或者N是P的右孩子)。

操作:P、S变色,并交换----相当于AVL中的右右中旋转即以P为中心S向左旋(或者是AVL中的左左中的旋转),未结束。
解析:我们知道P的左边少了一个黑节点,这样操作相当于在N头上又加了一个红节点----不违反任何性质,但是到通过N的路径仍少了一个黑节点,需要再把对N进行一次检索,并作相应的操作才可以平衡(暂且不管往下看)。
情形2:P、S及S的孩子们都为黑。

操作:S改为红色,未结束。
解析:S变为红色后经过S节点的路径的黑节点数目也减少了1,那个从P出发到其叶子节点到所有路径所包含的黑节点数目(记为num)相等了。但是这个num比之前少了1,因为左右子树中的黑节点数目都减少了!一般地,P是他父节点G的一个孩子,那么由G到其叶子节点的黑节点数目就不相等了,所以说没有结束,需把P当做新的起始点开始向上检索。
情形3:P为红(S一定为黑),S的孩子们都为黑。

操作:P该为黑,S改为红,结束。
解析:这种情况最简单了,既然N这边少了一个黑节点,那么S这边就拿出了一个黑节点来共享一下,这样一来,S这边没少一个黑节点,而N这边便多了一个黑节点,这样就恢复了平衡,多么美好的事情哈!
情形4:P任意色,S为黑,N是P的左孩子,S的右孩子SR为红,S的左孩子任意(或者是N是P的右孩子,S的左孩子为红,S的右孩子任意)。

操作:SR(SL)改为黑,P改为黑,S改为P的颜色,P、S变换--这里相对应于AVL中的右右中的旋转(或者是AVL中的左左旋转),结束。
解析:P、S旋转有变色,等于给N这边加了一个黑节点,P位置(是位置而不是P)的颜色不变,S这边少了一个黑节点;SR有红变黑,S这边又增加了一个黑节点;这样一来又恢复了平衡,结束。
情形5:P任意色,S为黑,N是P的左孩子,S的左孩子SL为红,S的右孩子SR为黑(或者N是P的有孩子,S的右孩子为红,S的左孩子为黑)。

操作:SL(或SR)改为黑,S改为红,SL(SR)、S变换;此时就回到了情形4,SL(SR)变成了黑S,S变成了红SR(SL),做情形4的操作即可,这两次变换,其实就是对应AVL的右左的两次旋转(或者是AVL的左右的两次旋转)。
解析:这种情况如果你按情形4的操作的话,由于SR本来就是黑色,你无法弥补由于P、S的变换(旋转)给S这边造成的损失!所以我没先对S、SL进行变换之后就变为情形4的情况了,何乐而不为呢?
树的旋转知识
当我们在对红黑树进行插入和删除等操作时,对树做了修改,那么可能会违背红黑树的性质。
为了保持红黑树的性质,我们可以通过对树进行旋转,即修改树种某些结点的颜色及指针结构,以达到对红黑树进行
插入、删除结点等操作时,红黑树依然能保持它特有的性质(如上文所述的,五点性质)。
树的旋转,分为左旋和右旋,以下借助图来做形象的解释和介绍:
1.左旋

如上图所示:
当在某个结点pivot上,做左旋操作时,我们假设它的右孩子y不是NIL[T],pivot可以为树内任意右孩子而不是NIL[T]的结点。
左旋以pivot到y之间的链为“支轴”进行,它使y成为该孩子树新的根,而y的左孩子b则成为pivot的右孩子。
来看算法导论对此操作的算法实现(以x代替上述的pivot):
LEFT-ROTATE(T, x)
1 y ← right[x] ▹ Set y.
2 right[x] ← left[y] ▹ Turn y's
left subtree into x's right subtree.
3 p[left[y]] ← x
4 p[y] ← p[x] ▹ Link x's
parent to y.
5 if p[x] = nil[T]
6 then root[T] ← y
7 else if x = left[p[x]]
8 then left[p[x]] ← y
9 else right[p[x]] ← y
10 left[y] ← x ▹ Put x on y's
left.
11 p[x] ← y
2.右旋
右旋与左旋差不多,再此不做详细介绍。

对于树的旋转,能保持不变的只有原树的搜索性质,而原树的红黑性质则不能保持,
在红黑树的数据插入和删除后可利用旋转和颜色重涂来恢复树的红黑性质。
至于有些书如 STL源码剖析有对双旋的描述,其实双旋只是单旋的两次应用,并无新的内容,
因此这里就不再介绍了,而且左右旋也是相互对称的,只要理解其中一种旋转就可以了。
三、红黑树插入、删除操作的具体实现
三、I、ok,接下来,咱们来具体了解红黑树的插入操作。
向一棵含有n个结点的红黑树插入一个新结点的操作可以在O(lgn)时间内完成。
算法导论:
RB-INSERT(T, z)
1 y ← nil[T]
2 x ← root[T]
3 while x ≠ nil[T]
4 do y ← x
5 if key[z] < key[x]
6 then x ← left[x]
7 else x ← right[x]
8 p[z] ← y
9 if y = nil[T]
10 then root[T] ← z
11 else if key[z] < key[y]
12 then left[y] ← z
13 else right[y] ← z
14 left[z] ← nil[T]
15 right[z] ← nil[T]
16 color[z] ← RED
17 RB-INSERT-FIXUP(T, z)
咱们来具体分析下,此段代码:
RB-INSERT(T, z),将z插入红黑树T 之内。
为保证红黑性质在插入操作后依然保持,上述代码调用了一个辅助程序RB-INSERT-FIXUP
来对结点进行重新着色,并旋转。
14 left[z] ← nil[T]
15 right[z] ← nil[T] //保持正确的树结构
第16行,将z着为红色,由于将z着为红色可能会违背某一条红黑树的性质,
所以,在第17行,调用RB-INSERT-FIXUP(T,z)来保持红黑树的性质。
RB-INSERT-FIXUP(T, z),如下所示:
1 while color[p[z]] = RED
2 do if p[z] = left[p[p[z]]]
3 then y ← right[p[p[z]]]
4 if color[y] = RED
5 then color[p[z]] ← BLACK ▹ Case 1
6 color[y] ← BLACK ▹ Case 1
7 color[p[p[z]]] ← RED ▹ Case 1
8 z ← p[p[z]] ▹ Case 1
9 else if z = right[p[z]]
10 then z ← p[z] ▹ Case 2
11 LEFT-ROTATE(T, z) ▹ Case 2
12 color[p[z]] ← BLACK ▹ Case 3
13 color[p[p[z]]] ← RED ▹ Case 3
14 RIGHT-ROTATE(T, p[p[z]]) ▹ Case 3
15 else (same as then clause
with "right" and "left" exchanged)
16 color[root[T]] ← BLACK
情况1:插入的是根结点。
原树是空树,此情况只会违反性质2。
对策:直接把此结点涂为黑色。
情况2:插入的结点的父结点是黑色。
此不会违反性质2和性质4,红黑树没有被破坏。
对策:什么也不做。
情况3:当前结点的父结点是红色且祖父结点的另一个子结点(叔叔结点)是红色。
此时父结点的父结点一定存在,否则插入前就已不是红黑树。
与此同时,又分为父结点是祖父结点的左子还是右子,对于对称性,我们只要解开一个方向就可以了。
在此,我们只考虑父结点为祖父左子的情况。
同时,还可以分为当前结点是其父结点的左子还是右子,但是处理方式是一样的。我们将此归为同一类。
对策:将当前节点的父节点和叔叔节点涂黑,祖父结点涂红,把当前结点指向祖父节点,从新的当前节点重新开始算法。
针对情况3,变化前(图片来源:saturnman)[插入4节点]:

变化后:

情况4:当前节点的父节点是红色,叔叔节点是黑色,当前节点是其父节点的右子
对策:当前节点的父节点做为新的当前节点,以新当前节点为支点左旋。
如下图所示,变化前[插入7节点]:

变化后:

情况5:当前节点的父节点是红色,叔叔节点是黑色,当前节点是其父节点的左子
解法:父节点变为黑色,祖父节点变为红色,在祖父节点为支点右旋
如下图所示[插入2节点]

变化后:

==================
三、II、ok,接下来,咱们最后来了解,红黑树的删除操作:
算法导论一书,给的算法实现:
RB-DELETE(T, z) 单纯删除结点的总操作
1 if left[z] = nil[T] or right[z] = nil[T]
2 then y ← z
3 else y ← TREE-SUCCESSOR(z)
4 if left[y] ≠ nil[T]
5 then x ← left[y]
6 else x ← right[y]
7 p[x] ← p[y]
8 if p[y] = nil[T]
9 then root[T] ← x
10 else if y = left[p[y]]
11 then left[p[y]] ← x
12 else right[p[y]] ← x
13 if y 3≠ z
14 then key[z] ← key[y]
15 copy y's satellite data into z
16 if color[y] = BLACK
17 then RB-DELETE-FIXUP(T, x)
18 return y
RB-DELETE-FIXUP(T, x) 恢复与保持红黑性质的工作
1 while x ≠ root[T] and color[x] = BLACK
2 do if x = left[p[x]]
3 then w ← right[p[x]]
4 if color[w] = RED
5 then color[w] ← BLACK ▹ Case 1
6 color[p[x]] ← RED ▹ Case 1
7 LEFT-ROTATE(T, p[x]) ▹ Case 1
8 w ← right[p[x]] ▹ Case 1
9 if color[left[w]] = BLACK and color[right[w]] = BLACK
10 then color[w] ← RED ▹ Case 2
11 x p[x] ▹ Case 2
12 else if color[right[w]] = BLACK
13 then color[left[w]] ← BLACK ▹ Case 3
14 color[w] ← RED ▹ Case 3
15 RIGHT-ROTATE(T, w) ▹ Case 3
16 w ← right[p[x]] ▹ Case 3
17 color[w] ← color[p[x]] ▹ Case 4
18 color[p[x]] ← BLACK ▹ Case 4
19 color[right[w]] ← BLACK ▹ Case 4
20 LEFT-ROTATE(T, p[x]) ▹ Case 4
21 x ← root[T] ▹ Case 4
22 else (same as then clause with "right" and "left" exchanged)
23 color[x] ← BLACK
情况1:当前节点是红色
解法,直接把当前节点染成黑色,结束。
此时红黑树性质全部恢复。
情况2:当前节点是黑色且是根节点
解法:什么都不做,结束
情况3:当前节点是黑色,且兄弟节点为红色(此时父节点和兄弟节点的子节点分为黑)。
解法:把父节点染成红色,把兄弟结点染成黑色,之后重新进入算法(我们只讨论当前节点是其父节点左孩子时的情况)。
然后,针对父节点做一次左旋。此变换后原红黑树性质5不变,而把问题转化为兄弟节点为黑色的情况。
3.变化前:

3.变化后:

情况4:当前节点是黑色,且兄弟是黑色,且兄弟节点的两个子节点全为黑色。
解法:把当前节点和兄弟节点中抽取一重黑色追加到父节点上,把父节点当成新的当前节点,重新进入算法。(此变换后性质5不变)
4.变化前

4.变化后

情况5:当前节点颜色是黑色,兄弟节点是黑色,兄弟的左子是红色,右子是黑色。
解法:把兄弟结点染红,兄弟左子节点染黑,之后再在兄弟节点为支点解右旋,
之后重新进入算法。此是把当前的情况转化为情况6,而性质5得以保持。
5.变化前:

5.变化后:

情况6:当前节点颜色是黑色,它的兄弟节点是黑色,但是兄弟节点的右子是红色,兄弟节点左子的颜色任意。
解法:把兄弟节点染成当前节点父节点的颜色,把当前节点父节点染成黑色,兄弟节点右子染成黑色,
之后以当前节点的父节点为支点进行左旋,此时算法结束,红黑树所有性质调整正确。
6.变化前:

6.变化后:

