[POJ 1222]EXTENDED LIGHTS OUT(高斯消元)
2014-08-20 11:20
351 查看
EXTENDED LIGHTS OUT
Description
In an extended version of the game Lights Out, is a puzzle with 5 rows of 6 buttons each (the actual puzzle has 5 rows of 5 buttons each). Each button has a light. When a button is pressed, that button and each of its (up to four)
neighbors above, below, right and left, has the state of its light reversed. (If on, the light is turned off; if off, the light is turned on.) Buttons in the corners change the state of 3 buttons; buttons on an edge change the state of 4 buttons and other
buttons change the state of 5. For example, if the buttons marked X on the left below were to be pressed,the display would change to the image on the right.
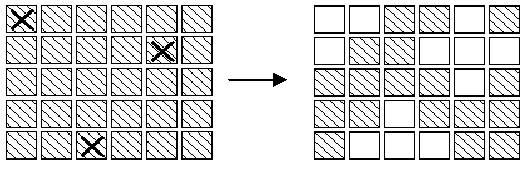
The aim of the game is, starting from any initial set of lights on in the display, to press buttons to get the display to a state where all lights are off. When adjacent buttons are pressed, the action of one button can undo the effect of another. For instance,
in the display below, pressing buttons marked X in the left display results in the right display.Note that the buttons in row 2 column 3 and row 2 column 5 both change the state of the button in row 2 column 4,so that, in the end, its state is unchanged.
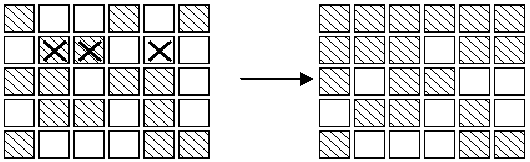
Note:
1. It does not matter what order the buttons are pressed.
2. If a button is pressed a second time, it exactly cancels the effect of the first press, so no button ever need be pressed more than once.
3. As illustrated in the second diagram, all the lights in the first row may be turned off, by pressing the corresponding buttons in the second row. By repeating this process in each row, all the lights in the first
four rows may be turned out. Similarly, by pressing buttons in columns 2, 3 ?, all lights in the first 5 columns may be turned off.
Write a program to solve the puzzle.
Input
The first line of the input is a positive integer n which is the number of puzzles that follow. Each puzzle will be five lines, each of which has six 0 or 1 separated by one or more spaces. A 0 indicates that the light is off,
while a 1 indicates that the light is on initially.
Output
For each puzzle, the output consists of a line with the string: "PUZZLE #m", where m is the index of the puzzle in the input file. Following that line, is a puzzle-like display (in the same format as the input) . In this case,
1's indicate buttons that must be pressed to solve the puzzle, while 0 indicate buttons, which are not pressed. There should be exactly one space between each 0 or 1 in the output puzzle-like display.
Sample Input
Sample Output
Source
Greater New York 2002

XOR方程组高斯消元,和POJ 1830解法相同,只不过灯由一行变成多行,对于多行的灯,给每个灯一个编号即可,使得每个坐标上的灯是否被按下的状态都对应列向量x中的一个元素,这个细节打表就可以了,列向量C(方程常数)的初始值为灯的终止状态,最后高斯消元你们懂的。
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 6608 | Accepted: 4355 |
In an extended version of the game Lights Out, is a puzzle with 5 rows of 6 buttons each (the actual puzzle has 5 rows of 5 buttons each). Each button has a light. When a button is pressed, that button and each of its (up to four)
neighbors above, below, right and left, has the state of its light reversed. (If on, the light is turned off; if off, the light is turned on.) Buttons in the corners change the state of 3 buttons; buttons on an edge change the state of 4 buttons and other
buttons change the state of 5. For example, if the buttons marked X on the left below were to be pressed,the display would change to the image on the right.

The aim of the game is, starting from any initial set of lights on in the display, to press buttons to get the display to a state where all lights are off. When adjacent buttons are pressed, the action of one button can undo the effect of another. For instance,
in the display below, pressing buttons marked X in the left display results in the right display.Note that the buttons in row 2 column 3 and row 2 column 5 both change the state of the button in row 2 column 4,so that, in the end, its state is unchanged.

Note:
1. It does not matter what order the buttons are pressed.
2. If a button is pressed a second time, it exactly cancels the effect of the first press, so no button ever need be pressed more than once.
3. As illustrated in the second diagram, all the lights in the first row may be turned off, by pressing the corresponding buttons in the second row. By repeating this process in each row, all the lights in the first
four rows may be turned out. Similarly, by pressing buttons in columns 2, 3 ?, all lights in the first 5 columns may be turned off.
Write a program to solve the puzzle.
Input
The first line of the input is a positive integer n which is the number of puzzles that follow. Each puzzle will be five lines, each of which has six 0 or 1 separated by one or more spaces. A 0 indicates that the light is off,
while a 1 indicates that the light is on initially.
Output
For each puzzle, the output consists of a line with the string: "PUZZLE #m", where m is the index of the puzzle in the input file. Following that line, is a puzzle-like display (in the same format as the input) . In this case,
1's indicate buttons that must be pressed to solve the puzzle, while 0 indicate buttons, which are not pressed. There should be exactly one space between each 0 or 1 in the output puzzle-like display.
Sample Input
2 0 1 1 0 1 0 1 0 0 1 1 1 0 0 1 0 0 1 1 0 0 1 0 1 0 1 1 1 0 0 0 0 1 0 1 0 1 0 1 0 1 1 0 0 1 0 1 1 1 0 1 1 0 0 0 1 0 1 0 0
Sample Output
PUZZLE #1 1 0 1 0 0 1 1 1 0 1 0 1 0 0 1 0 1 1 1 0 0 1 0 0 0 1 0 0 0 0 PUZZLE #2 1 0 0 1 1 1 1 1 0 0 0 0 0 0 0 1 0 0 1 1 0 1 0 1 1 0 1 1 0 1
Source
Greater New York 2002

XOR方程组高斯消元,和POJ 1830解法相同,只不过灯由一行变成多行,对于多行的灯,给每个灯一个编号即可,使得每个坐标上的灯是否被按下的状态都对应列向量x中的一个元素,这个细节打表就可以了,列向量C(方程常数)的初始值为灯的终止状态,最后高斯消元你们懂的。
#include <iostream>
#include <cstring>
#include <cmath>
#include <algorithm>
#define MAXN 100
using namespace std;
int A[MAXN][MAXN],n=30,m=30; //n=矩阵行数,m=矩阵列数
int pos[5][6]={
{0,1,2,3,4,5},
{6,7,8,9,10,11},
{12,13,14,15,16,17},
{18,19,20,21,22,23},
{24,25,26,27,28,29}
};
bool inMap(int x,int y) //判断(x,y)是否在矩阵里
{
if(x<0||x>=5||y<0||y>=6) return false;
return true;
}
void work()
{
for(int i=0;i<5;i++)
for(int j=0;j<6;j++)
{
int now=pos[i][j];
A[now][now]=1;
if(inMap(i-1,j))
A[pos[i-1][j]][now]=1;
if(inMap(i+1,j))
A[pos[i+1][j]][now]=1;
if(inMap(i,j-1))
A[pos[i][j-1]][now]=1;
if(inMap(i,j+1))
A[pos[i][j+1]][now]=1;
}
}
void Gauss()
{
int i=0,j=0,k,l,index;
while(i<n&&j<m+1)
{
//交换行i与行index
//选index行
index=i;
for(k=i+1;k<n;k++)
if(abs(A[k][j])>abs(A[index][j]))
index=k;
if(A[index][j]!=0)
{
//交换
if(index!=i)
for(k=j;k<m+1;k++)
swap(A[i][k],A[index][k]);
//消元
for(k=0;k<n;k++)
if(k!=i&&A[k][j]!=0)
for(l=j;l<m+1;l++)
A[k][l]^=A[i][l];
i++;
}
j++;
}
}
int main()
{
int N;
cin>>N;
for(int Case=1;Case<=N;Case++)
{
for(int i=0;i<5;i++)
for(int j=0;j<6;j++)
{
cin>>A[pos[i][j]]
;
}
work();
Gauss();
cout<<"PUZZLE #"<<Case<<endl;
for(int i=0;i<5;i++)
{
for(int j=0;j<6;j++)
{
cout<<A[pos[i][j]]
<<' ';
}
cout<<endl;
}
}
return 0;
}
相关文章推荐
- 【高斯消元】Poj 1222:EXTENDED LIGHTS OUT
- [POJ1222]EXTENDED LIGHTS OUT(高斯消元)
- POJ 1222 EXTENDED LIGHTS OUT 高斯消元
- POJ 1222 EXTENDED LIGHTS OUT 二进制高斯消元 (开关翻转问题)
- poj1222--EXTENDED LIGHTS OUT(高斯消元)
- POJ 1222 EXTENDED LIGHTS OUT(高斯消元)
- POJ 1222 EXTENDED LIGHTS OUT(高斯消元)
- poj 1222 EXTENDED LIGHTS OUT(高斯消元)
- POJ 1222 EXTENDED LIGHTS OUT(高斯消元解XOR方程组)
- poj 1222 EXTENDED LIGHTS OUT (高斯消元)
- poj1222 EXTENDED LIGHTS OUT 高斯消元
- POJ 1222 EXTENDED LIGHTS OUT(高斯消元)
- poj 1222 EXTENDED LIGHTS OUT(高斯消元)
- poj 1222 EXTENDED LIGHTS OUT(数学:高斯消元||爆搜:DFS)
- poj 1222 EXTENDED LIGHTS OUT (高斯消元)
- 【POJ】1222 EXTENDED LIGHTS OUT(高斯消元)
- poj 1222 EXTENDED LIGHTS OUT 【高斯消元】
- POJ 1222 EXTENDED LIGHTS OUT 【高斯消元】
- poj1222 EXTENDED LIGHTS OUT(高斯消元)
- poj 1222 EXTENDED LIGHTS OUT(高斯消元)
