ISTA & FISTA
2014-08-03 04:38
92 查看
LASSO是一个图像处理中经典的目标方程

第二项的1范数限制了x的稀疏性。

比如在图像去模糊的问题中,已知模糊的图像b,和模糊函数R,我们想恢复去模糊的图像I。这些变量的关系可以表达成I*R=b,其中*为卷积。在理想状态下,b没有任何噪音,那么这个问题就很简单。基于卷积定理,两个函数在时域的卷积相当于频域的相乘,那么我们只需要求出b和R的傅里叶变换,然后相除得到I的傅里叶变换,再将其恢复到时域。但是一般来说模糊图像b含有噪声,这使得频域中的操作异常不稳定,所以更多时候,我们希望通过以下方程求得I
)
其中模糊算子R表现成矩阵形式,I和b表示为1维向量,函数p作为规范项。我们将I小波分解,I=Wx,其中W为小波基,x为小波基系数。我们知道图像的小波表示是稀疏的,那么目标方程就变成了LASSO的形式

其中A=RW。现在的问题是,这个方程由于L1范数的存在,不是处处可微的,如果用subgradient的方法,收敛的速度会很慢。
ISTA(Iterative Shrinkage-Thresholding Algorithm)
这个算法可以解决以上f+g形式的最小化问题,但ISTA适用于以下形式问题的求解:1.目标方程是f+g的形式2.f和g是凸的,f是可导的,g无所谓3.g需要足够简单(可拆分的,可以做坐标下降的coordinate descent)我们首先看对f做一般的递归下降
)
这种形式的递归下降可以写成等价的以下形式(general form)
&space;+&space;\left&space;\langle&space;x-x_{k-1},\nabla&space;f(x_{k-1})&space;\right&space;\rangle&space;+&space;{1&space;\over&space;2t_k}\left&space;\|&space;x-x_{k-1}&space;\right&space;\|^2\})
因为在我们的问题中除了f还有一个非平滑的g存在,一个简单的想法是改变迭代公式成以下形式(也就是直接把g加到后面)
&space;+&space;\left&space;\langle&space;x-x_{k-1},\nabla&space;f(x_{k-1})&space;\right&space;\rangle&space;+&space;{1&space;\over&space;2t_k}\left&space;\|&space;x-x_{k-1}&space;\right&space;\|^2+g(x)\})
通过基本的代数,消去和x无关的常数项,每一步的迭代公式就变成了
)&space;\right&space;\|^2+g(x)\})
这时我们可以看到,假如g是一个开拆分的函数(比如L1范数),我们就可以对每一维分别进行坐标下降,也就是将N维的最小值问题,转化成N个1D的最小值问题。我们发现,如果
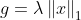
的话,那么这个问题有解析解,即每步的迭代可以写成:
))
其中
_i=(\left&space;|&space;x_i&space;\right&space;|-\alpha)_+sign(x_i))
称作shrinkage
operator。
FISTA(FAST Iterative Shrinkage-Thresholding Algorithm)
FISTA其实就是对ISTA应用Nestrerov加速。一个普通的Nestrerov加速递归下降的迭代步骤是
1.

2.

3.
)
4.
y_{k}+\gamma_ky_{k-1})
应用到FISTA上的话,就是把第3步换成ISTA的迭代步骤。可以证明FISTA可以达到

的收敛速度。(t是迭代次数)通过下面的实验可以看到,同样迭代了300次,左图(ISTA)仍未收敛,图像仍然模糊。而右图(FISTA)已经基本还原了去模糊的原图。


第二项的1范数限制了x的稀疏性。

比如在图像去模糊的问题中,已知模糊的图像b,和模糊函数R,我们想恢复去模糊的图像I。这些变量的关系可以表达成I*R=b,其中*为卷积。在理想状态下,b没有任何噪音,那么这个问题就很简单。基于卷积定理,两个函数在时域的卷积相当于频域的相乘,那么我们只需要求出b和R的傅里叶变换,然后相除得到I的傅里叶变换,再将其恢复到时域。但是一般来说模糊图像b含有噪声,这使得频域中的操作异常不稳定,所以更多时候,我们希望通过以下方程求得I
其中模糊算子R表现成矩阵形式,I和b表示为1维向量,函数p作为规范项。我们将I小波分解,I=Wx,其中W为小波基,x为小波基系数。我们知道图像的小波表示是稀疏的,那么目标方程就变成了LASSO的形式
其中A=RW。现在的问题是,这个方程由于L1范数的存在,不是处处可微的,如果用subgradient的方法,收敛的速度会很慢。
ISTA(Iterative Shrinkage-Thresholding Algorithm)
这个算法可以解决以上f+g形式的最小化问题,但ISTA适用于以下形式问题的求解:1.目标方程是f+g的形式2.f和g是凸的,f是可导的,g无所谓3.g需要足够简单(可拆分的,可以做坐标下降的coordinate descent)我们首先看对f做一般的递归下降
这种形式的递归下降可以写成等价的以下形式(general form)
因为在我们的问题中除了f还有一个非平滑的g存在,一个简单的想法是改变迭代公式成以下形式(也就是直接把g加到后面)
通过基本的代数,消去和x无关的常数项,每一步的迭代公式就变成了
这时我们可以看到,假如g是一个开拆分的函数(比如L1范数),我们就可以对每一维分别进行坐标下降,也就是将N维的最小值问题,转化成N个1D的最小值问题。我们发现,如果
的话,那么这个问题有解析解,即每步的迭代可以写成:
其中
称作shrinkage
operator。
FISTA(FAST Iterative Shrinkage-Thresholding Algorithm)
FISTA其实就是对ISTA应用Nestrerov加速。一个普通的Nestrerov加速递归下降的迭代步骤是
1.
2.
3.
4.
应用到FISTA上的话,就是把第3步换成ISTA的迭代步骤。可以证明FISTA可以达到
的收敛速度。(t是迭代次数)通过下面的实验可以看到,同样迭代了300次,左图(ISTA)仍未收敛,图像仍然模糊。而右图(FISTA)已经基本还原了去模糊的原图。


相关文章推荐
- FISTA的由来:从梯度下降法到ISTA & FISTA
- TDD & Patterns Notes
- Biztalk发布web服务时遭遇"SOAP内部处理失败"错误
- 关于"^"号的解释
- 一次表单提交失败 --- 内的name="action"的元素引起
- ADO.NET的数据提供程序和数据连接——ADO.NET学习&应用笔记之二
- 把&#编码转换成字符
- Android HttpClient && HttpPost简单使用
- Adwords Campaign network & placement
- Ubuntu右键添加"以管理员身份打开","在终端中打开"
- 【HTML5】'data-'属性的作用是什么?
- JSTL <fmt:formatDate/>
- Openerp Web PDF Report Preview & Print 简介
- SSIS 之 Exception "Cannot insert duplicate key in object..."
- 解决ADB server didn't ACK问题
- android&nbsp;SD卡自动挂载
- nefu 2 猜想(素数&&筛选)
- 【按住你的心】——Android开发CheckBox&RadioButton控件的简单使用
- IDOC 基本步骤
- Fedora 13 字符界面和图…
