【比特币】椭圆曲线数字签名算法-ECDSA
2014-07-17 10:44
267 查看
参考:
https://github.com/openssl/openssl/blob/master/crypto/ecdsa/ecdsa.h
原理篇:
http://kakaroto.homelinux.net/2012/01/how-the-ecdsa-algorithm-works/
实验篇:
http://www.nilsschneider.net/2013/01/28/recovering-bitcoin-private-keys.html
Makefile
Code:
测试:
HASH=0xaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa; // 20个字节的0xaa
比特币目前使用ECDSA对货币的所有权进行鉴定,当然前提是对于付款地址是椭圆曲线算法的公钥(secp256k1 for bitcoin)。
如果是puzzle类型等非标准的付款方式,那么resolve的方式就不是签名/验证的形式了,那就要看脚本的设置到底需要什么的推理前提了。
关于签名算法的细节可以参考wiki上bob&alice的签名验证例子。
比特币的源代码使用CECKey结构对openssl的ec算法进行了封装。
在此基础上衍生了其他密钥管理对象,CPubKey, CKeyID, CScriptID, CPrivKey, CKey

CKey可以导入通过SetPrivKey()/GetPrivKey()导入/导出openssl格式的私钥。
CKey可以通过GetPubKey()导出公钥(压缩格式或者非压缩格式的,根据内部标记来决定)
CKey可以通过Sign()来签署消息摘要
CPubKey可以通过GetID()调用来计算得到该公钥对应的索引(也就是该公钥的hash256/ripemd160的hash)
CPubKey可以通过Verify()来验证CKey的签名
CScript可以通过GetID()来获取序列化的脚本的索引(hash值)
可以以base58格式操作2类钱包地址;
地址可以是脚本,也可以是公钥,对应的分别是脚本的id和公钥的id,CSriptID, CPubKeyID
可以以base58格式操作私钥。
openssl ecdsa算法实践
1) 列举所有已经实现的算法曲线
比特币选取了
以下内容转载自原理篇
To popular demand, I have decided to try and explain how the ECDSA algorithm
works. I’ve been struggling a bit to understand it properly and while I found a lot of documentation about it, I haven’t really found any “ECDSA for newbies” anywhere. So I thought it would be good to explain in simple terms how it works so others can learn
from my research. I have found some websites that explain the basic principles but nowhere near enough to actually understand it, others that explains things without any basics, making it incomprehensible, and others that go way too deep into the the mathematics
behind it.
ECDSA stands for “Elliptic Curve Digital Signature Algorithm”, it’s used to create a digital
signatureof data (a file for example) in order to allow you to verify its authenticity without compromising its security. Think of it like a real signature, you can recognize someone’s signature, but you can’t forge it without others knowing. The ECDSA
algorithm is basically all about mathematics.. so I think it’s important to start by saying : “hey kids, don’t slack off at school, listen to your teachers, that stuff might be useful for you some day!”

But
these maths are fairly complicated, so while I’ll try to vulgarize it and make it understandable for non technical people, you will still probably need some knowledge in mathematics to understand it properly. I will do this in two parts, one that is a sort
of high level explanation about how it works, and another where I dig deeper into its inner workings to complete your understanding. Note however that I’ve just recently learned this stuff, so I’m definitely not an expert on the matter.
So the principle is simple, you have a mathematical equation which draws a curve on a graph, and you choose a random point on that curve and consider that your point of origin. Then you generate a random number, this is your private key, you do some magical
mathematical equation using that random number and that “point of origin” and you get a second point on the curve, that’s your public key. When you want to sign a file, you will use this private key (the random number) with a hash of the file (a unique number
to represent the file) into a magical equation and that will give you your signature. The signature itself is divided into two parts, called R and S.
In order to verify that the signature is correct, you only need the public key (that point on the curve that was generated using the private key) and you put that into another magical equation with one part of the signature (S),
and if it was signed correctly using the the private key, it will give you the other part of the signature (R).
So to make it short, a signature consists of two numbers, R and S,
and you use a private key to generate R and S,
and if a mathematical equation using the public key and Sgives
you R, then the signature
is valid. There is no way to know the private key or to create a signature using only the public key.
Alright, now for the more in depth understanding, I suggest you take an aspirin right now as this might hurt!

Let’s start with the basics (which may be boring for people who know about it, but is mandatory for those who don’t) : ECDSA uses only integer mathematics, there are no floating points (this means possible values are 1, 2, 3, etc.. but not 1.5..), also, the
range of the numbers is bound by how many bits are used in the signature (more bits means higher numbers, means more security as it becomes harder to ‘guess’ the critical numbers used in the equation), as you should know, computers use ‘bits’ to represent
data, a bit is a ‘digit’ in binary notation (0 and 1) and 8 bits represent one byte. Every time you add one bit, the maximum number that can be represented doubles, with 4 bits you can represent values 0 to 15 (for a total of 16 possible values), with 5 bits,
you can represent 32 values, with 6 bits, you can represent 64 values, etc.. one byte (8 bits) can represent 256 values, and 32 bits can represent 4294967296 values (4 Giga).. Usually ECDSA will use 160 bits total, so that makes… well, a very huge number with
49 digits in it…
ECDSA is used with a SHA1 cryptographic
hash of the message to sign (the file). A hash is
simply another mathematical equation that you apply on every byte of data which will give you a number that is unique to your data. Like for example, the sum of the values of all bytes may be considered a very dumb hash function. So if anything changes in
the message (the file) then the hash will be completely different. In the case of the SHA1 hash algorithm, it will always be 20 bytes (160 bits). It’s very useful to validate that a file has not been modified or corrupted, you get the 20 bytes hash for a file
of any size, and you can easily recalculate that hash to make sure it matches. What ECDSA signs is actually that hash, so if the data changes, the hash changes, and the signature isn’t valid anymore.
Now, how does it work? Well Elliptic
Curve cryptography is based on an equation of the form :
y^2 = (x^3 + a * x + b) mod p
First thing you notice is that there is a modulo and that the ‘y‘
is a square. This means that for anyx coordinate,
you will have two values of y and
that the curve is symmetric on the X axis. The modulo is a prime number and makes sure that all the values are within our range of 160 bits
and it allows the use of “modular
square root” and “modular
multiplicative inverse” mathematics which make calculating stuff easier (I think). Since we have a modulo (p)
, it means that the possible values of y^2 are
between 0 and p-1,
which gives us p total
possible values. However, since we are dealing with integers, only a smaller subset of those values will be a “perfect
square” (the square value of two integers), which gives us N possible
points on the curve where N < p (N being
the number of perfect squares between 0 and p).
Since each x will
yield two points (positive and negative values of the square-root of y^2),
this means that there are N/2 possible
‘x‘ coordinates that
are valid and that give a point on the curve. So this elliptic curve has a finite number of points on it, and it’s all because of the integer calculations and the modulus. Another thing you need to know about Elliptic
curves, is the notion of “point
addition“. It is defined as adding one point P to
another point Q will
lead to a point S such
that if you draw a line from P to Q,
it will intersect the curve on a third point R which
is the negative value of S (remember
that the curve is symmetric on the X axis). In this case, we define R
= -S to represent the symmetrical point of R on
the X axis. This is easier to illustrate with an image :
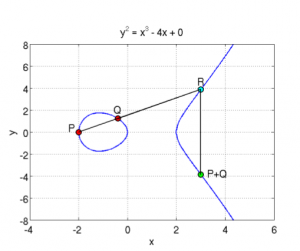
So
you can see a curve of the form y^2
= x^3 + ax + b (where a
= -4 and b = 0),
which is symmetric on the X axis, and where P+Q is
the symmetrical point through X of the point R which
is the third intersection of a line going from P to Q.
In the same manner, if you do P
+ P, it will be the symmetrical point of R which
is the intersection of the line that is a tangent to the point P..
AndP + P + P is the
addition between the resulting point of P+P with
the point P since P
+ P + P can be written as (P+P)
+ P.. This defines the “point
multiplication” where k*P is
the addition of the point P to
itself k times… here
are two examples showing this :
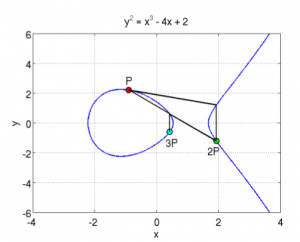
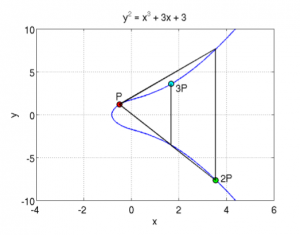
Here, you can see two elliptic curves, and a point P from
which you draw the tangent, it intersects the curve with a third point, and its symmetric point it 2P,
then from there, you draw a line from 2Pand P and
it will intersect the curve, and the symmetrical point is 3P.
etc… you can keep doing that for the point multiplication. You can also already guess why you need to take the symmetric point of R when
doing the addition, otherwise, multiple additions of the same point will always give the same line and the same three intersections.
One particularity of this point multiplication is that if you have a point R
= k*P, where you know Rand
you know P, there
is no way to find out what the value of ‘k‘
is. Since there is no point subtraction or point division, you cannot just resolve k
= R/P. Also, since you could be doing millions of point additions, you will just end up on another point on the curve, and you’d have no way of knowing “how” you got there. You can’t reverse this operation, and you can’t find the value ‘k‘
which was multiplied with your point P to
give you the resulting point R.
This thing where you can’t find the multiplicand even when you know the original and destination points is the whole basis of the security behind the ECDSA algorithm, and the principle is called a “trap
door function“.
Now that we’ve handled the “basics”, let’s talk about the actual ECDSA signature algorithm. For ECDSA, you first need to know your curve parameters, those are a,
b, p, N and G.
You already know that ‘a‘
and ‘b‘ are the parameters
of the curve function (y^2 = x^3
+ ax + b), that ‘p‘
is the prime modulus, and that ‘N‘
is the number of points of the curve, but there is also ‘G‘
that is needed for ECDSA, and it represents a ‘reference point’ or a point of origin if you prefer. Those curve parameters are important and without knowing them, you obviously can’t sign or verify a signature. Yes, verifying a signature isn’t just about knowing
the public key, you also need to know the curve parameters for which this public key is derived from.
So first of all, you will have a private and a public key.. the private key is a random number (of 20 bytes) that is generated, and the public key is a point on the curve generated from the point multiplication of G with
the private key. We set ‘dA‘
as the private key (random number) and ‘Qa‘
as the public key (a point), so we have : Qa
= dA * G (where G is
the point of reference in the curve parameters).
So how do you sign a file/message ? First, you need to know that the signature is 40 bytes and is represented by two values of 20 bytes each, the first one is called R and
the second one is called S..
so the pair (R, S) together
is your ECDSA signature.. now here’s how you can create those two values in order to sign a file.. first you must generate a random value ‘k‘
(of 20 byes), and use point multiplication to calculate the point P=k*G.
That point’s x value
will represent ‘R‘.
Since the point on the curve P is
represented by its (x, y) coordinates
(each being 20 bytes long), you only need the ‘x‘
value (20 bytes) for the signature, and that value will be called ‘R‘.
Now all you need is the ‘S‘
value.
To calculate S, you
must make a SHA1 hash of the message, this gives you a 20 bytes value that you will consider as a very huge integer number and we’ll call it ‘z‘.
Now you can calculate S using
the equation :
S = k^-1 (z + dA * R) mod p
Note here the k^-1 which
is the ‘modular
multiplicative inverse‘ of k…
it’s basically the inverse ofk,
but since we are dealing with integer numbers, then that’s not possible, so it’s a number such that (k^-1
* k ) mod p is equal to 1. And again, I remind you that k is
the random number used to generate R, z is
the hash of the message to sign, dA is
the private key and R is
the x coordinate ofk*G (where G is
the point of origin of the curve parameters).
Now that you have your signature, you want to verify it, it’s also quite simple, and you only need the public key (and curve parameters of course) to do that. You use this equation to calculate a point P :
P= S^-1*z*G + S^-1 * R * Qa
If the x coordinate
of the point P is
equal to R, that means
that the signature is valid, otherwise it’s not.
Pretty simple, huh? now let’s see why and how… and this is going to require some mathematics to verify :
We have :
P = S^-1*z*G + S^-1 * R *Qa
but Qa = dA*G, so:
P = S^-1*z*G + S^-1 * R * dA*G =
S^-1 (z + dA* R) * G
But the x coordinate
of P must match R and R is
the x coordinate of k
* G, which means that :
k*G = S^-1 (z + dA * R) *G
we can simplify by removing G which
gives us :
k = S^-1(z + dA * R)
by inverting k and S,
we get :
S = k^-1 (z + dA *R)
and that is the equation used to generate the signature.. so it matches, and that is the reason why you can verify the signature with it.
You can note that you need both ‘k‘
(random number) and ‘dA‘
(the private key) in order to calculate S,
but you only need R and Qa (public
key) to validate the signature. And since R=k*G andQa
= dA*G and because of the trap door function in the ECDSA point multiplication (explained above), we cannot calculate dA or k from
knowing Qa and R,
this makes the ECDSA algorithm secure, there is no way of finding the private keys, and there is no way of faking a signature without knowing the private key.
The ECDSA algorithm is used everywhere and has not been cracked and it is a vital part of most of today’s security.
Now I’ll discuss on how and why the ECDSA signatures that Sony used in the PS3 were faulty and how it allowed us to gain access to their private key.
So you remember the equations needed to generate a signature.. R
= k*G and S= k^-1(z
+ dA*R) mod p.. well this equation’s strength is in the fact that you have one equation with two unknowns (k and dA)
so there is no way to determine either one of those. However, the security of the algorithm is based on its implementation and it’s important to make sure that ‘k‘
is randomly generated and that there is no way that someone can guess, calculate, or use a timing attack or any other type of attack in order to find the random value ‘k‘.
But Sony made a huge mistake in their implementation, they used the same value for ‘k‘
everywhere, which means that if you have two signatures, both with the same k,
then they will both have the same R value,
and it means that you can calculate k using
two S signatures of
two files with hashes z and z’ and
signatures S and S’respectively
:
S – S’ = k^-1 (z + dA*R) – k^-1 (z’
+ da*R) = k^-1 (z + da*R – z’ -dA*R) = k^-1 (z – z’)
So : k = (z – z’) / (S – S’)
Once you know k, then
the equation for S because
one equation with one unknown and is then easily resolved for dA :
dA = (S*k – z) / R
Once you know the private key dA,
you can now sign your files and the PS3 will recognize it as an authentic file signed by Sony. This is why it’s important to make sure that the random number used for generating the signature is actually “cryptographically random”. This is also the reason
why it is impossible to have a custom firmware above 3.56, simply because since the 3.56 version, Sony have fixed their ECDSA algorithm implementation and used new keys for which it is impossible to find the private key.. if there was a way to find that key,
then the security of every computer, website, system may be compromised since a lot of systems are relying on ECDSA for their security, and it is impossible to crack.
Finally! I hope this makes the whole algorithm clearer to many of you.. I know that this is still very complicated and hard to understand. I usually try to make things easy to understand for non technical people, but this algorithm is too complex to be able
to explain in any simpler terms. After all that’s why I prefer to call it the MFET algorithm (Mathematics For Extra Terrestrials)

But if you are a developer or a mathematician or someone interested in learning about this because you want to help or simple gain knowledge, then I’m sure that this contains enough information for you to get started or to at least understand the concept behind
this unknown beast called “ECDSA”.
That being said, I’d like to thank a few people who helped me understand all of this, one particularly who wishes to remain anonymous, as well as the many wikipedia pages I linked to throughout this article, and Avi Kak thanks to his
paper explaining the mathematics behind ECDSA, and from which I have taken those graph images aboves.
P.s: In this article, I used ’20 bytes’ in my text to talk about the ECDSA signature because that’s what is usually used as it matches the SHA1 hash size of 20 bytes and that’s what the PS3 security uses, but the algorithm itself can be used with any size of
numbers. There may be other inaccuracies in this article, but like I said, I’m not an expert, I just barely learned all of this in the past week.
以下内容转载在实验篇:
On December 25th of last year I discovered a potential weakness in some Bitcoin implementations. Have a look at this transaction:
This transactions has two inputs and one output. If you look closely at the two input scripts you will notice there are quite a few equal bytes at the start and at the end. Those bytes at the end is the hex-encoded public key of the address spending the coins
so there’s nothing wrong with that. However, the first half of the script is the actual signature (r, s):
As you can see, r1 equals r2. This is a huge problem. We’ll be able to recover the private key
to this public key:
We just need to find z1 and z2! These are the hashes of the outputs to be signed. Let’s fetch the output transations and calculate them (it is calculated by OP_CHECKSIG):
That’s it. Let’s setup our sage notebook like this:
p is just the order of G, a parameter of the secp256k1 curve used by Bitcoin. Let’s create a field for our calculations:
And calculate the private key within this field:
Convert it to a more suitable format:
And import it to your favourite Bitcoin wallet. It’ll calculate the correct bitcoin address and you’ll be able to spend coins send to this address.
There are a few vulnerable bitcoin addresses in the blockchain. After some research I was able to contact the owner of this address. He allowed me to spend the funds.
Why did this work? ECDSA requires a random number for each signature. If this random number is ever used twice with the same private key it can be recovered. This transaction was generated by a hardware bitcoin wallet using a pseudo-random number generator
that was returning the same “random” number every time.
https://github.com/openssl/openssl/blob/master/crypto/ecdsa/ecdsa.h
原理篇:
http://kakaroto.homelinux.net/2012/01/how-the-ecdsa-algorithm-works/
实验篇:
http://www.nilsschneider.net/2013/01/28/recovering-bitcoin-private-keys.html
Makefile
.PHONY:all all: gcc -I/d/workspace/github/altcoin/bitcoin-3rd/ssl/include -o sigvery -g -O0 sigvery.c -L/d/workspace/github/altcoin/bitcoin-3rd/ssl/lib -lssl -lcrypto -lgdi32
Code:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <openssl/opensslconf.h>
#include <openssl/ec.h>
#include <openssl/bn.h>
#include <openssl/ecdsa.h>
int main(int argc, char * argv []){
// First step: create a EC_KEY object (note: this part is not ECDSA specific)
int ret;
int nid;
ECDSA_SIG *sig;
EC_KEY *eckey;
unsigned char digest [20];
memset(digest, 0xaa, sizeof(digest));// 测试用的假HASH
nid = OBJ_sn2nid("secp256k1");
eckey = EC_KEY_new_by_curve_name(nid);
if (eckey == NULL)
{
/* error */
perror("EC_KEY_new_by_curve_name");
}
if (!EC_KEY_generate_key(eckey))
{
/* error */
}
else
{// 打印一下ec的私钥和公钥
EC_KEY_print_fp(stdout, eckey, 0);
}
// Second step: compute the ECDSA signature of a SHA-1 hash value using ECDSA_do_sign
sig = ECDSA_do_sign(digest, 20, eckey);// 签名
if (sig == NULL)
{
/* error */
perror("ECDSA_do_sign");
}
else
{// 打印一下签名,r和s
printf("Signature:\n\tr=%s\n\ts=%s\n", BN_bn2hex(sig->r), BN_bn2hex(sig->s));
}
// Third step: verify the created ECDSA signature using ECDSA_do_verify
ret = ECDSA_do_verify(digest, 20, sig, eckey);// 验证
if (ret == -1)
{
/* error */
perror("ECDSA_do_verify");
}
else if (ret == 0)
{
/* incorrect signature */
printf("Verified Failure\n");
}
else /* ret == 1 */
{
/* signature ok */
printf("Verified OK\n");
}
return 0;
}测试:
HASH=0xaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa; // 20个字节的0xaa
$ ./sigvery.exe Private-Key: (256 bit) priv: 00:95:55:33:26:d8:92:cd:58:d7:7b:71:b8:02:29: 36:41:9a:22:e9:f0:21:72:02:a7:fc:1e:05:a3:f5: 6e:f4:ec pub: 04:76:91:81:fd:2e:44:e0:17:03:b3:53:7d:55:fe: e2:f5:6a:89:d1:5b:2c:e2:06:83:6a:e5:64:b6:4b: 07:76:8c:8b:df:57:7b:75:7b:f6:fb:9c:44:6f:1b: f6:56:ff:ac:ed:2f:65:a9:49:81:ba:af:90:13:8f: 96:a3:9e:83:9f Field Type: prime-field Prime: 00:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff: ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:fe:ff: ff:fc:2f A: 0 B: 7 (0x7) Generator (uncompressed): 04:79:be:66:7e:f9:dc:bb:ac:55:a0:62:95:ce:87: 0b:07:02:9b:fc:db:2d:ce:28:d9:59:f2:81:5b:16: f8:17:98:48:3a:da:77:26:a3:c4:65:5d:a4:fb:fc: 0e:11:08:a8:fd:17:b4:48:a6:85:54:19:9c:47:d0: 8f:fb:10:d4:b8 Order: 00:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff:ff: ff:fe:ba:ae:dc:e6:af:48:a0:3b:bf:d2:5e:8c:d0: 36:41:41 Cofactor: 1 (0x1) Signature: r=F0AB42A05A1C7CB18EF50A0E63CF287B3604A3741D6875DADE9031E648055E7D s=4C556EDC930313C67286A7B7AD7BC336FB39C0BA4BC42BE801FBBE8CBDCD0012 Verified OK
比特币目前使用ECDSA对货币的所有权进行鉴定,当然前提是对于付款地址是椭圆曲线算法的公钥(secp256k1 for bitcoin)。
如果是puzzle类型等非标准的付款方式,那么resolve的方式就不是签名/验证的形式了,那就要看脚本的设置到底需要什么的推理前提了。
关于签名算法的细节可以参考wiki上bob&alice的签名验证例子。
比特币的源代码使用CECKey结构对openssl的ec算法进行了封装。
在此基础上衍生了其他密钥管理对象,CPubKey, CKeyID, CScriptID, CPrivKey, CKey

1) CKey
对openssl中的ecdsa算法的基本封装,是整个算法的核心。CKey可以导入通过SetPrivKey()/GetPrivKey()导入/导出openssl格式的私钥。
// Initialize from a CPrivKey (serialized OpenSSL private key data). bool SetPrivKey(const CPrivKey &vchPrivKey, bool fCompressed);
// Convert the private key to a CPrivKey (serialized OpenSSL private key data). // This is expensive. CPrivKey GetPrivKey() const;
CKey可以通过GetPubKey()导出公钥(压缩格式或者非压缩格式的,根据内部标记来决定)
// Compute the public key from a private key. // This is expensive. CPubKey GetPubKey() const;
CKey可以通过Sign()来签署消息摘要
// Create a DER-serialized signature. bool Sign(const uint256 &hash, std::vector<unsigned char>& vchSig) const;
2) CPubKey
对openssl中的ecdsa算法的公钥的基本封装,可以由CKey的成员函数计算得到。CPubKey可以通过GetID()调用来计算得到该公钥对应的索引(也就是该公钥的hash256/ripemd160的hash)
// Get the KeyID of this public key (hash of its serialization)
CKeyID GetID() const {
return CKeyID(Hash160(vch, vch+size()));
}CPubKey可以通过Verify()来验证CKey的签名
// Verify a DER signature (~72 bytes). // If this public key is not fully valid, the return value will be false. bool Verify(const uint256 &hash, const std::vector<unsigned char>& vchSig) const;
3)CScript
对支付脚本的状态机的封装CScript可以通过GetID()来获取序列化的脚本的索引(hash值)
CScriptID GetID() const
{
return CScriptID(Hash160(*this));
}4)CScriptID
支付脚本script的索引的封装,20字节hash值5) CPubKeyID
支付公钥的索引的封装, 20字节hash值6)CBitcoinAddress
版本和索引值的封装可以以base58格式操作2类钱包地址;
地址可以是脚本,也可以是公钥,对应的分别是脚本的id和公钥的id,CSriptID, CPubKeyID
7) CBitCoinSecret
对私钥base58格式的封装可以以base58格式操作私钥。
openssl ecdsa算法实践
1) 列举所有已经实现的算法曲线
gentoobox harrywu # openssl ecparam -list_curves secp112r1 : SECG/WTLS curve over a 112 bit prime field secp112r2 : SECG curve over a 112 bit prime field secp128r1 : SECG curve over a 128 bit prime field secp128r2 : SECG curve over a 128 bit prime field secp160k1 : SECG curve over a 160 bit prime field secp160r1 : SECG curve over a 160 bit prime field secp160r2 : SECG/WTLS curve over a 160 bit prime field secp192k1 : SECG curve over a 192 bit prime field secp224k1 : SECG curve over a 224 bit prime field secp224r1 : NIST/SECG curve over a 224 bit prime field secp256k1 : SECG curve over a 256 bit prime field secp384r1 : NIST/SECG curve over a 384 bit prime field secp521r1 : NIST/SECG curve over a 521 bit prime field prime192v1: NIST/X9.62/SECG curve over a 192 bit prime field prime192v2: X9.62 curve over a 192 bit prime field prime192v3: X9.62 curve over a 192 bit prime field prime239v1: X9.62 curve over a 239 bit prime field prime239v2: X9.62 curve over a 239 bit prime field prime239v3: X9.62 curve over a 239 bit prime field prime256v1: X9.62/SECG curve over a 256 bit prime field sect113r1 : SECG curve over a 113 bit binary field sect113r2 : SECG curve over a 113 bit binary field sect131r1 : SECG/WTLS curve over a 131 bit binary field sect131r2 : SECG curve over a 131 bit binary field sect163k1 : NIST/SECG/WTLS curve over a 163 bit binary field sect163r1 : SECG curve over a 163 bit binary field sect163r2 : NIST/SECG curve over a 163 bit binary field sect193r1 : SECG curve over a 193 bit binary field sect193r2 : SECG curve over a 193 bit binary field sect233k1 : NIST/SECG/WTLS curve over a 233 bit binary field sect233r1 : NIST/SECG/WTLS curve over a 233 bit binary field sect239k1 : SECG curve over a 239 bit binary field sect283k1 : NIST/SECG curve over a 283 bit binary field sect283r1 : NIST/SECG curve over a 283 bit binary field sect409k1 : NIST/SECG curve over a 409 bit binary field sect409r1 : NIST/SECG curve over a 409 bit binary field sect571k1 : NIST/SECG curve over a 571 bit binary field sect571r1 : NIST/SECG curve over a 571 bit binary field c2pnb163v1: X9.62 curve over a 163 bit binary field c2pnb163v2: X9.62 curve over a 163 bit binary field c2pnb163v3: X9.62 curve over a 163 bit binary field c2pnb176v1: X9.62 curve over a 176 bit binary field c2tnb191v1: X9.62 curve over a 191 bit binary field c2tnb191v2: X9.62 curve over a 191 bit binary field c2tnb191v3: X9.62 curve over a 191 bit binary field c2pnb208w1: X9.62 curve over a 208 bit binary field c2tnb239v1: X9.62 curve over a 239 bit binary field c2tnb239v2: X9.62 curve over a 239 bit binary field c2tnb239v3: X9.62 curve over a 239 bit binary field c2pnb272w1: X9.62 curve over a 272 bit binary field c2pnb304w1: X9.62 curve over a 304 bit binary field c2tnb359v1: X9.62 curve over a 359 bit binary field c2pnb368w1: X9.62 curve over a 368 bit binary field c2tnb431r1: X9.62 curve over a 431 bit binary field wap-wsg-idm-ecid-wtls1: WTLS curve over a 113 bit binary field wap-wsg-idm-ecid-wtls3: NIST/SECG/WTLS curve over a 163 bit binary field wap-wsg-idm-ecid-wtls4: SECG curve over a 113 bit binary field wap-wsg-idm-ecid-wtls5: X9.62 curve over a 163 bit binary field wap-wsg-idm-ecid-wtls6: SECG/WTLS curve over a 112 bit prime field wap-wsg-idm-ecid-wtls7: SECG/WTLS curve over a 160 bit prime field wap-wsg-idm-ecid-wtls8: WTLS curve over a 112 bit prime field wap-wsg-idm-ecid-wtls9: WTLS curve over a 160 bit prime field wap-wsg-idm-ecid-wtls10: NIST/SECG/WTLS curve over a 233 bit binary field wap-wsg-idm-ecid-wtls11: NIST/SECG/WTLS curve over a 233 bit binary field wap-wsg-idm-ecid-wtls12: WTLS curvs over a 224 bit prime field Oakley-EC2N-3: IPSec/IKE/Oakley curve #3 over a 155 bit binary field. Not suitable for ECDSA. Questionable extension field! Oakley-EC2N-4: IPSec/IKE/Oakley curve #4 over a 185 bit binary field. Not suitable for ECDSA. Questionable extension field!
比特币选取了
secp256k1 : SECG curve over a 256 bit prime field
以下内容转载自原理篇
To popular demand, I have decided to try and explain how the ECDSA algorithm
works. I’ve been struggling a bit to understand it properly and while I found a lot of documentation about it, I haven’t really found any “ECDSA for newbies” anywhere. So I thought it would be good to explain in simple terms how it works so others can learn
from my research. I have found some websites that explain the basic principles but nowhere near enough to actually understand it, others that explains things without any basics, making it incomprehensible, and others that go way too deep into the the mathematics
behind it.
ECDSA stands for “Elliptic Curve Digital Signature Algorithm”, it’s used to create a digital
signatureof data (a file for example) in order to allow you to verify its authenticity without compromising its security. Think of it like a real signature, you can recognize someone’s signature, but you can’t forge it without others knowing. The ECDSA
algorithm is basically all about mathematics.. so I think it’s important to start by saying : “hey kids, don’t slack off at school, listen to your teachers, that stuff might be useful for you some day!”
But
these maths are fairly complicated, so while I’ll try to vulgarize it and make it understandable for non technical people, you will still probably need some knowledge in mathematics to understand it properly. I will do this in two parts, one that is a sort
of high level explanation about how it works, and another where I dig deeper into its inner workings to complete your understanding. Note however that I’ve just recently learned this stuff, so I’m definitely not an expert on the matter.
So the principle is simple, you have a mathematical equation which draws a curve on a graph, and you choose a random point on that curve and consider that your point of origin. Then you generate a random number, this is your private key, you do some magical
mathematical equation using that random number and that “point of origin” and you get a second point on the curve, that’s your public key. When you want to sign a file, you will use this private key (the random number) with a hash of the file (a unique number
to represent the file) into a magical equation and that will give you your signature. The signature itself is divided into two parts, called R and S.
In order to verify that the signature is correct, you only need the public key (that point on the curve that was generated using the private key) and you put that into another magical equation with one part of the signature (S),
and if it was signed correctly using the the private key, it will give you the other part of the signature (R).
So to make it short, a signature consists of two numbers, R and S,
and you use a private key to generate R and S,
and if a mathematical equation using the public key and Sgives
you R, then the signature
is valid. There is no way to know the private key or to create a signature using only the public key.
Alright, now for the more in depth understanding, I suggest you take an aspirin right now as this might hurt!
Let’s start with the basics (which may be boring for people who know about it, but is mandatory for those who don’t) : ECDSA uses only integer mathematics, there are no floating points (this means possible values are 1, 2, 3, etc.. but not 1.5..), also, the
range of the numbers is bound by how many bits are used in the signature (more bits means higher numbers, means more security as it becomes harder to ‘guess’ the critical numbers used in the equation), as you should know, computers use ‘bits’ to represent
data, a bit is a ‘digit’ in binary notation (0 and 1) and 8 bits represent one byte. Every time you add one bit, the maximum number that can be represented doubles, with 4 bits you can represent values 0 to 15 (for a total of 16 possible values), with 5 bits,
you can represent 32 values, with 6 bits, you can represent 64 values, etc.. one byte (8 bits) can represent 256 values, and 32 bits can represent 4294967296 values (4 Giga).. Usually ECDSA will use 160 bits total, so that makes… well, a very huge number with
49 digits in it…
ECDSA is used with a SHA1 cryptographic
hash of the message to sign (the file). A hash is
simply another mathematical equation that you apply on every byte of data which will give you a number that is unique to your data. Like for example, the sum of the values of all bytes may be considered a very dumb hash function. So if anything changes in
the message (the file) then the hash will be completely different. In the case of the SHA1 hash algorithm, it will always be 20 bytes (160 bits). It’s very useful to validate that a file has not been modified or corrupted, you get the 20 bytes hash for a file
of any size, and you can easily recalculate that hash to make sure it matches. What ECDSA signs is actually that hash, so if the data changes, the hash changes, and the signature isn’t valid anymore.
Now, how does it work? Well Elliptic
Curve cryptography is based on an equation of the form :
y^2 = (x^3 + a * x + b) mod p
First thing you notice is that there is a modulo and that the ‘y‘
is a square. This means that for anyx coordinate,
you will have two values of y and
that the curve is symmetric on the X axis. The modulo is a prime number and makes sure that all the values are within our range of 160 bits
and it allows the use of “modular
square root” and “modular
multiplicative inverse” mathematics which make calculating stuff easier (I think). Since we have a modulo (p)
, it means that the possible values of y^2 are
between 0 and p-1,
which gives us p total
possible values. However, since we are dealing with integers, only a smaller subset of those values will be a “perfect
square” (the square value of two integers), which gives us N possible
points on the curve where N < p (N being
the number of perfect squares between 0 and p).
Since each x will
yield two points (positive and negative values of the square-root of y^2),
this means that there are N/2 possible
‘x‘ coordinates that
are valid and that give a point on the curve. So this elliptic curve has a finite number of points on it, and it’s all because of the integer calculations and the modulus. Another thing you need to know about Elliptic
curves, is the notion of “point
addition“. It is defined as adding one point P to
another point Q will
lead to a point S such
that if you draw a line from P to Q,
it will intersect the curve on a third point R which
is the negative value of S (remember
that the curve is symmetric on the X axis). In this case, we define R
= -S to represent the symmetrical point of R on
the X axis. This is easier to illustrate with an image :

So
you can see a curve of the form y^2
= x^3 + ax + b (where a
= -4 and b = 0),
which is symmetric on the X axis, and where P+Q is
the symmetrical point through X of the point R which
is the third intersection of a line going from P to Q.
In the same manner, if you do P
+ P, it will be the symmetrical point of R which
is the intersection of the line that is a tangent to the point P..
AndP + P + P is the
addition between the resulting point of P+P with
the point P since P
+ P + P can be written as (P+P)
+ P.. This defines the “point
multiplication” where k*P is
the addition of the point P to
itself k times… here
are two examples showing this :


Here, you can see two elliptic curves, and a point P from
which you draw the tangent, it intersects the curve with a third point, and its symmetric point it 2P,
then from there, you draw a line from 2Pand P and
it will intersect the curve, and the symmetrical point is 3P.
etc… you can keep doing that for the point multiplication. You can also already guess why you need to take the symmetric point of R when
doing the addition, otherwise, multiple additions of the same point will always give the same line and the same three intersections.
One particularity of this point multiplication is that if you have a point R
= k*P, where you know Rand
you know P, there
is no way to find out what the value of ‘k‘
is. Since there is no point subtraction or point division, you cannot just resolve k
= R/P. Also, since you could be doing millions of point additions, you will just end up on another point on the curve, and you’d have no way of knowing “how” you got there. You can’t reverse this operation, and you can’t find the value ‘k‘
which was multiplied with your point P to
give you the resulting point R.
This thing where you can’t find the multiplicand even when you know the original and destination points is the whole basis of the security behind the ECDSA algorithm, and the principle is called a “trap
door function“.
Now that we’ve handled the “basics”, let’s talk about the actual ECDSA signature algorithm. For ECDSA, you first need to know your curve parameters, those are a,
b, p, N and G.
You already know that ‘a‘
and ‘b‘ are the parameters
of the curve function (y^2 = x^3
+ ax + b), that ‘p‘
is the prime modulus, and that ‘N‘
is the number of points of the curve, but there is also ‘G‘
that is needed for ECDSA, and it represents a ‘reference point’ or a point of origin if you prefer. Those curve parameters are important and without knowing them, you obviously can’t sign or verify a signature. Yes, verifying a signature isn’t just about knowing
the public key, you also need to know the curve parameters for which this public key is derived from.
So first of all, you will have a private and a public key.. the private key is a random number (of 20 bytes) that is generated, and the public key is a point on the curve generated from the point multiplication of G with
the private key. We set ‘dA‘
as the private key (random number) and ‘Qa‘
as the public key (a point), so we have : Qa
= dA * G (where G is
the point of reference in the curve parameters).
So how do you sign a file/message ? First, you need to know that the signature is 40 bytes and is represented by two values of 20 bytes each, the first one is called R and
the second one is called S..
so the pair (R, S) together
is your ECDSA signature.. now here’s how you can create those two values in order to sign a file.. first you must generate a random value ‘k‘
(of 20 byes), and use point multiplication to calculate the point P=k*G.
That point’s x value
will represent ‘R‘.
Since the point on the curve P is
represented by its (x, y) coordinates
(each being 20 bytes long), you only need the ‘x‘
value (20 bytes) for the signature, and that value will be called ‘R‘.
Now all you need is the ‘S‘
value.
To calculate S, you
must make a SHA1 hash of the message, this gives you a 20 bytes value that you will consider as a very huge integer number and we’ll call it ‘z‘.
Now you can calculate S using
the equation :
S = k^-1 (z + dA * R) mod p
Note here the k^-1 which
is the ‘modular
multiplicative inverse‘ of k…
it’s basically the inverse ofk,
but since we are dealing with integer numbers, then that’s not possible, so it’s a number such that (k^-1
* k ) mod p is equal to 1. And again, I remind you that k is
the random number used to generate R, z is
the hash of the message to sign, dA is
the private key and R is
the x coordinate ofk*G (where G is
the point of origin of the curve parameters).
Now that you have your signature, you want to verify it, it’s also quite simple, and you only need the public key (and curve parameters of course) to do that. You use this equation to calculate a point P :
P= S^-1*z*G + S^-1 * R * Qa
If the x coordinate
of the point P is
equal to R, that means
that the signature is valid, otherwise it’s not.
Pretty simple, huh? now let’s see why and how… and this is going to require some mathematics to verify :
We have :
P = S^-1*z*G + S^-1 * R *Qa
but Qa = dA*G, so:
P = S^-1*z*G + S^-1 * R * dA*G =
S^-1 (z + dA* R) * G
But the x coordinate
of P must match R and R is
the x coordinate of k
* G, which means that :
k*G = S^-1 (z + dA * R) *G
we can simplify by removing G which
gives us :
k = S^-1(z + dA * R)
by inverting k and S,
we get :
S = k^-1 (z + dA *R)
and that is the equation used to generate the signature.. so it matches, and that is the reason why you can verify the signature with it.
You can note that you need both ‘k‘
(random number) and ‘dA‘
(the private key) in order to calculate S,
but you only need R and Qa (public
key) to validate the signature. And since R=k*G andQa
= dA*G and because of the trap door function in the ECDSA point multiplication (explained above), we cannot calculate dA or k from
knowing Qa and R,
this makes the ECDSA algorithm secure, there is no way of finding the private keys, and there is no way of faking a signature without knowing the private key.
The ECDSA algorithm is used everywhere and has not been cracked and it is a vital part of most of today’s security.
Now I’ll discuss on how and why the ECDSA signatures that Sony used in the PS3 were faulty and how it allowed us to gain access to their private key.
So you remember the equations needed to generate a signature.. R
= k*G and S= k^-1(z
+ dA*R) mod p.. well this equation’s strength is in the fact that you have one equation with two unknowns (k and dA)
so there is no way to determine either one of those. However, the security of the algorithm is based on its implementation and it’s important to make sure that ‘k‘
is randomly generated and that there is no way that someone can guess, calculate, or use a timing attack or any other type of attack in order to find the random value ‘k‘.
But Sony made a huge mistake in their implementation, they used the same value for ‘k‘
everywhere, which means that if you have two signatures, both with the same k,
then they will both have the same R value,
and it means that you can calculate k using
two S signatures of
two files with hashes z and z’ and
signatures S and S’respectively
:
S – S’ = k^-1 (z + dA*R) – k^-1 (z’
+ da*R) = k^-1 (z + da*R – z’ -dA*R) = k^-1 (z – z’)
So : k = (z – z’) / (S – S’)
Once you know k, then
the equation for S because
one equation with one unknown and is then easily resolved for dA :
dA = (S*k – z) / R
Once you know the private key dA,
you can now sign your files and the PS3 will recognize it as an authentic file signed by Sony. This is why it’s important to make sure that the random number used for generating the signature is actually “cryptographically random”. This is also the reason
why it is impossible to have a custom firmware above 3.56, simply because since the 3.56 version, Sony have fixed their ECDSA algorithm implementation and used new keys for which it is impossible to find the private key.. if there was a way to find that key,
then the security of every computer, website, system may be compromised since a lot of systems are relying on ECDSA for their security, and it is impossible to crack.
Finally! I hope this makes the whole algorithm clearer to many of you.. I know that this is still very complicated and hard to understand. I usually try to make things easy to understand for non technical people, but this algorithm is too complex to be able
to explain in any simpler terms. After all that’s why I prefer to call it the MFET algorithm (Mathematics For Extra Terrestrials)
But if you are a developer or a mathematician or someone interested in learning about this because you want to help or simple gain knowledge, then I’m sure that this contains enough information for you to get started or to at least understand the concept behind
this unknown beast called “ECDSA”.
That being said, I’d like to thank a few people who helped me understand all of this, one particularly who wishes to remain anonymous, as well as the many wikipedia pages I linked to throughout this article, and Avi Kak thanks to his
paper explaining the mathematics behind ECDSA, and from which I have taken those graph images aboves.
P.s: In this article, I used ’20 bytes’ in my text to talk about the ECDSA signature because that’s what is usually used as it matches the SHA1 hash size of 20 bytes and that’s what the PS3 security uses, but the algorithm itself can be used with any size of
numbers. There may be other inaccuracies in this article, but like I said, I’m not an expert, I just barely learned all of this in the past week.
以下内容转载在实验篇:
Recovering Bitcoin private keys using weak signatures from the blockchain
On December 25th of last year I discovered a potential weakness in some Bitcoin implementations. Have a look at this transaction:transaction: 9ec4bc49e828d924af1d1029cacf709431abbde46d59554b62bc270e3b29c4b1 input script 1: 30440220d47ce4c025c35ec440bc81d99834a624875161a26bf56ef7fdc0f5d52f843ad1022044e1ff2dfd8102cf7a47c21d5c9fd5701610d04953c6836596b4fe9dd2f53e3e0104dbd0c61532279cf72981c3584fc32216e0127699635c2789f549e0730c059b81ae133016a69c21e23f1859a95f06d52b7bf149a8f2fe4e8535c8a829b449c5ff input script 2: 30440220d47ce4c025c35ec440bc81d99834a624875161a26bf56ef7fdc0f5d52f843ad102209a5f1c75e461d7ceb1cf3cab9013eb2dc85b6d0da8c3c6e27e3a5a5b3faa5bab0104dbd0c61532279cf72981c3584fc32216e0127699635c2789f549e0730c059b81ae133016a69c21e23f1859a95f06d52b7bf149a8f2fe4e8535c8a829b449c5ff
This transactions has two inputs and one output. If you look closely at the two input scripts you will notice there are quite a few equal bytes at the start and at the end. Those bytes at the end is the hex-encoded public key of the address spending the coins
so there’s nothing wrong with that. However, the first half of the script is the actual signature (r, s):
r1: d47ce4c025c35ec440bc81d99834a624875161a26bf56ef7fdc0f5d52f843ad1 r2: d47ce4c025c35ec440bc81d99834a624875161a26bf56ef7fdc0f5d52f843ad1 s1: 44e1ff2dfd8102cf7a47c21d5c9fd5701610d04953c6836596b4fe9dd2f53e3e s2: 9a5f1c75e461d7ceb1cf3cab9013eb2dc85b6d0da8c3c6e27e3a5a5b3faa5bab
As you can see, r1 equals r2. This is a huge problem. We’ll be able to recover the private key
to this public key:
private key = (z1*s2 - z2*s1)/(r*(s1-s2))
We just need to find z1 and z2! These are the hashes of the outputs to be signed. Let’s fetch the output transations and calculate them (it is calculated by OP_CHECKSIG):
z1: c0e2d0a89a348de88fda08211c70d1d7e52ccef2eb9459911bf977d587784c6e z2: 17b0f41c8c337ac1e18c98759e83a8cccbc368dd9d89e5f03cb633c265fd0ddc
That’s it. Let’s setup our sage notebook like this:
p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141 r = 0xd47ce4c025c35ec440bc81d99834a624875161a26bf56ef7fdc0f5d52f843ad1 s1 = 0x44e1ff2dfd8102cf7a47c21d5c9fd5701610d04953c6836596b4fe9dd2f53e3e s2 = 0x9a5f1c75e461d7ceb1cf3cab9013eb2dc85b6d0da8c3c6e27e3a5a5b3faa5bab z1 = 0xc0e2d0a89a348de88fda08211c70d1d7e52ccef2eb9459911bf977d587784c6e z2 = 0x17b0f41c8c337ac1e18c98759e83a8cccbc368dd9d89e5f03cb633c265fd0ddc
p is just the order of G, a parameter of the secp256k1 curve used by Bitcoin. Let’s create a field for our calculations:
K = GF(p)
And calculate the private key within this field:
K((z1*s2 - z2*s1)/(r*(s1-s2))) 88865298299719117682218467295833367085649033095698151055007620974294165995414
Convert it to a more suitable format:
hex: c477f9f65c22cce20657faa5b2d1d8122336f851a508a1ed04e479c34985bf96 WIF: 5KJp7KEffR7HHFWSFYjiCUAntRSTY69LAQEX1AUzaSBHHFdKEpQ
And import it to your favourite Bitcoin wallet. It’ll calculate the correct bitcoin address and you’ll be able to spend coins send to this address.
There are a few vulnerable bitcoin addresses in the blockchain. After some research I was able to contact the owner of this address. He allowed me to spend the funds.
Why did this work? ECDSA requires a random number for each signature. If this random number is ever used twice with the same private key it can be recovered. This transaction was generated by a hardware bitcoin wallet using a pseudo-random number generator
that was returning the same “random” number every time.
相关文章推荐
- 椭圆曲线数字签名算法(ECDSA)
- ecdsa 椭圆曲线数字签名算法
- Bitcoin学习篇之---Elliptic Curve Digital Signature Algorithm(椭圆曲线数字签名算法)
- [以太坊源代码分析] IV. 椭圆曲线密码学和以太坊中的椭圆曲线数字签名算法应用
- Jwt Token 安全策略使用 ECDSA 椭圆曲线加密算法签名/验证
- 【比特币】椭圆曲线密钥生成
- VS2008 椭圆曲线签名(ECDSA)
- OpenSSL: 椭圆曲线签名与校验 (ECDSA)
- 椭圆曲线公钥转换为比特币地址原理
- Android绘图机制(二)——自定义View绘制形, 圆形, 三角形, 扇形, 椭圆, 曲线,文字和图片的坐标讲解
- ECC-Elliptic Curves Cryptography,椭圆曲线密码编码学
- 数字签名算法_ECDSA
- iOS 2D绘图详解(Quartz 2D)之路径(点,直线,虚线,曲线,圆弧,椭圆,矩形)
- 万云BaaS | 椭圆曲线加密教程【上篇】
- Android利用canvas画各种图形(点、直线、弧、圆、椭圆、文字、矩形、多边形、曲线、圆角矩形)
- Android利用canvas画各种图形(点、直线、弧、圆、椭圆、文字、矩形、多边形、曲线、圆角矩形)
- Android利用canvas画各种图形(点、直线、弧、圆、椭圆、文字、矩形、多边形、曲线、圆角矩形)
- 20.openssl编程——椭圆曲线
- Raphael学习笔记(5)--绘图(路径【椭圆曲线】)
- Android利用canvas画各种图形(点、直线、弧、圆、椭圆、文字、矩形、多边形、曲线、圆角矩形)
