机器学习之支持向量机(svm)

浅谈svm

1写作原因：

本来网上关于svm的各种学习资料应有尽有，没有必要在大家面前班门弄斧，你也知道，svm本来知识点本来就一本书那么厚，岂是我三言两语能说清楚的，但最近在学svm，心得体会还是有一点的，所以想跟大家分享一下。而本人认为各种机器学算法之间联系甚密，我们应该比较着学习说不定能对算法有更深入的了解，于是就想写点东西，一是为了复习一下知识，二就是纯粹的聊以自嘲了。

2svm 和logistic

我们知道，最最基础的svm也是一种二分类器了，而我们的logistic regression也是一种二分类器，既然都是二分类器，难道就没一点联系吗?呵呵，我仔细比较了logistic regression和svm，还真的发现了点值得玩味的地方。首先看我们的logistic regression：逻辑回归中我们的分类为0，和1，我们,svm使用的结果标签是y=-1,y=1
，替换在logistic回归中使用的y=0和y=1。同时将

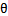
替换成w和b。以前的

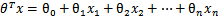
，其中认为

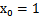
。现在我们替换

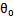
为b，后面替换

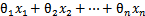
为

（即

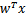
）。这样，我们让

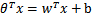
，进一步

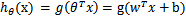
。也就是说除了y由y=0变为y=-1，只是标记不同外，与logistic回归的形式化表示没区别。再明确下假设函数

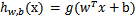
，我们在logistic
regression中g(z)是y = 1类时的概率，当时如果g(z)>0.5，其就是1类，反之为0类，那么我们这g(wx+b)是不是也可以是个什么映射，让其实现分类呢，当然可以，只不过我们不再去找一个什么logistic function去帮助我们实现(通过的是概率实现的)，而是一个平面。也就是wx+b = 0的超平面（我们将通过所谓的距离来实现，后面将）.下面让我们正式进入svm了。

3svm

svm简介：

如图：


如图5-21，针对于两个点，我们找一个平面去把方块和圆圈分开，可能会有无数个这样的平面，我们要找其中的最佳平面，使得距离超平面最近的点距离最大，也就是如下图的情况：



为了更好地理解不同的超平面对泛化误差的影响，考虑两个决策边界B1和B2，如图5-22所示。这两个决策边界都能准确无误地将训练样本划分到各自的类中。每个决策边界Bi都对应着一对超平面，分别记为bi1和bi2其中，bi1是这样得到的:平行移动一个和决策边界平行的超平面，在到触到最近的方块为止;类似地，平行移动一个和决策边界平行的超平面，直到触到最近的圆圈，可以得到bi2。这两个超平面之间的间距称为分类器的边缘。通过图5-22中的图解，注意到B1的边缘显著大于几的边缘。在这个例子中，B1就是训练练样本的最大边缘超平面，这也很好的解释了那句拗口的话，什么距离超平面最近的点距离最大，就是这个意思。
刚才我们已经提到过，这个超平面的方程是Wx + b = 0,那么我们容易得到，超平面一边的点Wx + b > 0,我们把这边的点标注于1类，反之标注为-1类，也就是：



可以看到这个和我们的逻辑回归中的g(z)是不是惊人的相似的呢，同时问题也来了，那么我们如何才能得到我们的w，和b呢，对于logistic regression，其是通过极大似然来学习的，那对于我们的svm怎么办，其实我在上述曾经提到过了，就是距离，我们在上面构筑了两个平行平面bi1,和bi2，显而易见，如果我们的bi1和bi2的距离越大，我们分类效果也就越好，所以我们假设bi1，bi2的方程是
Wx + b = 1,Wx + b = -1;(也许你会问，为什么要把它分为1 和 -1，能不能假设成其他的，当然可以，只是为了简便，因为我们的约束距离和这个因素实际上没关系，之后我再说明)，我们知道两平行平面的距离是2/||w||(什么，这个东西看不懂，假设H1:w1x1+w2x2=+1,H2:w1x1+w2x2=-1，那H1和H2的距离就是|1+1|/
sqrt(w12+w12)=2/||w||))我们要做的就是要让2/||w||最大化。

训练svm：

那么我们如何才能让我的2/||w||最大化呢，从我们的训练数据中训练W，b时候，我们的我们的参数必须满足下面这个条件：



如果我们想把这个式子写的更紧凑一点的化就是




这也就是为什么我们刚才选bi1,bi2时为什么会选Wx + b = 1，就是为了书写方便，所以我们的这个问题的目标就变成了，maxf(w) = 2/||w|| ,为了方便我们求解，我们把最终的目标形式定为:



很显然，这是一个凸二次规划问题，我们的目的就是通过学习算法，得到我们的w和b，这样就得到了我们的超平面，超平面一处，分类就是菜了。先别急着高兴。我们怎样才能得到目标函数的最小值呢？呵呵，为了避免大家看着无聊，先该大家一个例子，来证明我们的这个目标形式是可以实现分类的，我们来个小例子，之后我们再继续，例子如下：





不会吧，这就得到了答案，这额太简单了，是的，就是这么简单，再复杂的问题也是一个个简单问题积累而成的，通过本个小例子我们可以看出，所谓的支持向量其实就是我们yi(Wx+b) = 1上的点，也就是我们平行平面bi1，bi2上上面的点，得到我们的超平面后，我们怎么去分类呢，就比如说，上述X2是一个点，我们将其代入我们的超平面的1/2+1/2 -2=-1<0所以其应该是负类，事实证明也是这样的。当然这知识svm最最基础的东西，如果有这么简单就不会写成一本书，甚至成为一门学科了，这一篇暂时说到这，下一次我们就要将其复杂化了。