线性分类器之Fisher线性判别函数

Fisher判别是一种应用极为广泛的线性分类的方法，基本思想是：把

维空间的所有模式投影到一条过原点的直线上，即将模式的维数压缩到一维，并要求统一类型的样本尽可能多地聚集在一起，不同类型的样本尽可能地分开。

如下图所示，两类模式的分布，它们的投影不论在

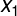
或

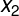
轴上都是混杂的，因此单纯取它们在

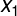
或

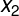
轴上的投影式不好分类的。但是，有可能存在一条直线AB，使得样本在它上面的投影很容易分开。


设给定两类模式的样本集

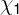
和

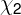
，它们有

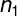
和

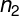
个

维的样本。我们的目标就是找到一条直线，使得模式样本在这条直线上的投影最有利于分类。设

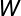
为这条直线正方向的单位向量，即

，于是有

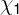
和

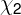
到直线的投影得到相应的集合

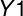
和

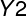
，其中每个

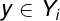
就是

在单位向量

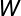
的投影。于是就有：



(1)
为了找到最有利于分类的方向

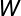
，需要建立一个准则函数，它能反映不同类别模式在这条直线投影分离程度的好坏。

为了使类别分离得好，应使各类模式投影均值彼此间的间距尽可能大。设

是第i类

维样本的均值：



(2)

则这些样本在直线

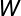
上的投影的均值是：



(3)
从而投影均值间的距离是：


(4)
因为

和

对于给定的两类样本集是不变的，所以只要改变

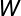
的方向，就可能改变投影均值间的距离。

为了使类别分离得好，还应使同类模式的投影比较密集。这里可以使用类内离散度来度量这个密集程度。定义一类模式投影的类内离散度(方差)为：



(5)

则两类的总的离散度为：



(6)

两类的类间离散度度为：



(7)

它代表了整个样本集合中各类样本投影的密集程度，为了得到更好的分类结果，应该选择直线

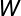
使得类内总的离散度尽可能小，类间离散度尽可能大。

综合上述考虑，构造Fisher判别函数：



(8)

它使得准则函数：



(9)

取得极大值。

将J(W)展开定义：

I.第i类离散度矩阵（协方差阵）



(10)

II.类内离散度矩阵：



(11)

III.类间离散度矩阵:



(12)

于是有





(13)

所以



(14)

又







(15)

根据上述推导，准则函数

可以改写为



(16)

利用Lagrange乘子法（拉格朗日乘子法），求取上式极大值，

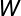
必须满足



(17)

(若

不可逆，使用SVD求解伪逆)(也可以采用梯度下降法迭代)

这就是使得准则函数

极大值解。

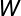
就是使得样本的投影在类间最分散，类内最集中地最优解。求取了

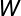
之后，任意待识别的样本

在

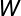
上的投影为



这样就可以将

维空间的样本降维都一维空间，即在直线

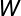
上变成一维样本

。

然后计算一维空间上分类的阈值。设训练样本的数量分别对应为

和

，对两类样本的均值进行加权平均可以得到分类阈值。这里有三种确定阈值的方法：

I.



II.



iii.



(18)

分类判别为



需要注意的是，这样得到的结果有一定局限，只是对准则函数最优，在许多情况下，结果不完全理想。另外它没有利用样本分布的信息，虽然计算简单，但是错误率不能达到最小。

由上可知，Fisher适合投影后线性可分的分类情况。